
- •Глава 4 Производная и дифференциал § 1. Производная. Механический и геометрический смысл производной
- •4. Односторонние производные.
- •§2. Понятие дифференцируемости функции
- •§ 3. Формулы и правила вычисления производных
- •7. Простейшие правила вычисления производных.
- •12. Формула для приращения функции.
- •13. Правило дифференцирования сложной функции.
- •14. Правила дифференцирования обратных функций.
- •§ 4. Дифференциал функции
- •2. Геометрический смысл дифференциала.
- •3. Сводка формул для дифференциалов.
- •4. Дифференциал сложной функции. Инвариантность формы дифференциала.
- •§ 5. Производные высших порядков
- •2. Формула Лейбница для производной n-го порядка от произведения двух функций.
- •3. Механическое истолкование второй производной.
- •§ 6. Дифференциалы высших порядков
- •§ 7. Дифференцирование функции, заданной параметрически
- •§ 8. Основные теоремы дифференциального исчисления
- •§ 9. Формула Тейлора
- •2. Примеры разложения по формуле Тейлора.
- •§ 10. Раскрытие неопределенностей по правилу Лопиталя
- •1. Неопределенность вида .
- •2. Неопределенность вида .
- •§ 11. Признаки постоянства, возрастания и убывания функций
- •§ 12. Теория экстремальных значений функции
- •2. Исследование стационарных критических точек функции с помощью второй производной.
- •§ 13. Характер выпуклости кривой. Точки перегиба
- •§ 14. Асимптоты кривой
- •§ 15. Построение графика функции по характерным точкам
12. Формула для приращения функции.
Пусть функция
![]() определена в промежутке Х
и пусть х0
— некоторая точка из X,
в которой существует конечная производная
определена в промежутке Х
и пусть х0
— некоторая точка из X,
в которой существует конечная производная
![]() .
Дадим
.
Дадим
![]() приращение
приращение
![]() — любое, но такое, что
— любое, но такое, что
![]() и точка
и точка
![]() .
Положим
.
Положим
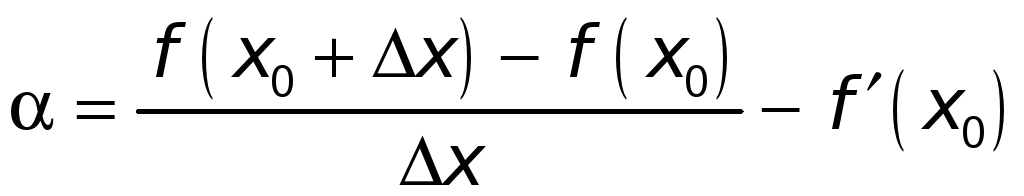 .
(*)
.
(*)
Ясно, что
![]() зависит от
зависит от
![]() ,
т. е.
,
т. е.
![]() ,
и что
,
и что
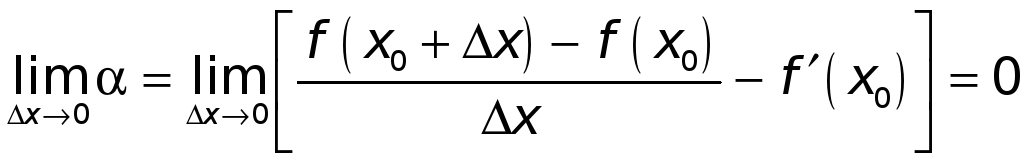 .
.
Из соотношения (*) находим
![]() ,
,
или
![]() .
(**)
.
(**)
Формула (**) и есть формула для приращения функции.
Замечание.
Формула (**) установлена для
![]() ,
ибо она выведена из (*), а соотношение
(*) теряет смысл при
,
ибо она выведена из (*), а соотношение
(*) теряет смысл при
![]() .
Если мы сами любым образом доопределим
функцию
.
Если мы сами любым образом доопределим
функцию
![]() в точке
в точке
![]() (например, положим
(например, положим
![]() или
или
![]() и т. д.), то формула (**) окажется верной и
для
и т. д.), то формула (**) окажется верной и
для
![]() .
Условимся раз и навсегда полагать
.
Условимся раз и навсегда полагать
![]() .
Тогда формула (**) будет верной как для
.
Тогда формула (**) будет верной как для
![]() ,
так и для
,
так и для
![]() и соотношение
и соотношение
![]() будет верно независимо от того, по какому
закону
будет верно независимо от того, по какому
закону
![]() (хотя бы
(хотя бы
![]() и принимало значение нуль).
и принимало значение нуль).
13. Правило дифференцирования сложной функции.
Пусть функция
![]() определена в промежутке
определена в промежутке
![]() ,
а функция
,
а функция
![]() определена в промежутке X
и такая, что если
определена в промежутке X
и такая, что если
![]() то
то
![]() .
Тогда для
.
Тогда для
![]() имеет смысл выражение
имеет смысл выражение
![]() (
(![]() — сложная функция). Предположим, что в
точке
— сложная функция). Предположим, что в
точке
![]() существует конечная производная
существует конечная производная
![]() ,
а в точке
,
а в точке
![]() (
(![]() )
существует конечная производная
)
существует конечная производная
![]() .
Покажем, что существует конечная
.
Покажем, что существует конечная
![]() и найдем ее.
и найдем ее.
Дадим х0
приращение
![]() — любое, но такое, что
— любое, но такое, что
![]() и точка
и точка
![]() .
Тогда функция
.
Тогда функция
![]() получит приращение
получит приращение
![]() (не исключено, что
(не исключено, что
![]() ).
).
Так как
![]() ,
то приращению
,
то приращению
![]() отвечает приращение
отвечает приращение
![]() .
.
По формуле приращения функции (**) (см. пункт 12)
![]() ,
,
где
![]() при
при
![]() .
А тогда
.
А тогда
![]() ,
,
Пусть
![]() .
Но тогда
.
Но тогда
![]() (ибо функция
(ибо функция
![]() дифференцируемая в точке х0,
а значит и непрерывная в точке х0).
А, следовательно, и
дифференцируемая в точке х0,
а значит и непрерывная в точке х0).
А, следовательно, и
![]() при
при
![]() .
Значит,
.
Значит,
![]() ,
,
т. е.
![]() .
Показано, таким образом, что
.
Показано, таким образом, что
![]() существует конечная и что
существует конечная и что
![]() (короче:
(короче:
![]() ).
).
Правило цепочки.
Производная сложной функции по независимой
переменной равна ее производной по
промежуточной переменной, умноженной
на производную промежуточной переменной
по независимой переменной. (Здесь
![]() — промежуточная переменная).
— промежуточная переменная).
Пример.
1)
![]() ,
где
,
где
![]() .
.
Имеем
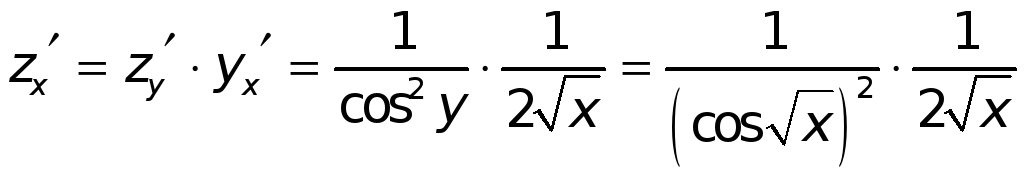 .
.
Правило.
Если для
получения значения
![]() нужно произвести над х
много действий, то для применения правила
цепочки следует обозначить через
нужно произвести над х
много действий, то для применения правила
цепочки следует обозначить через
![]() результат всех этих действий, кроме
последнего. Например,
результат всех этих действий, кроме
последнего. Например,
-
если
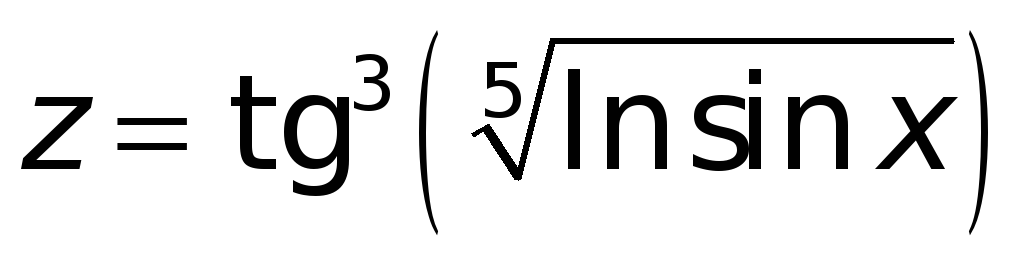 ,
то
,
то
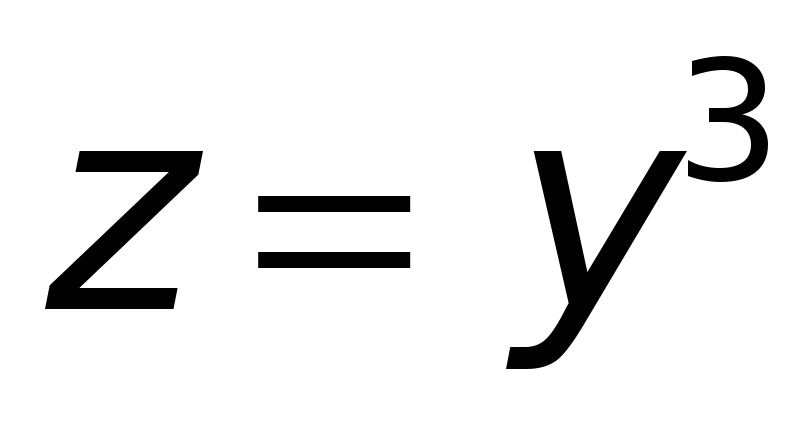 ,
где
,
где
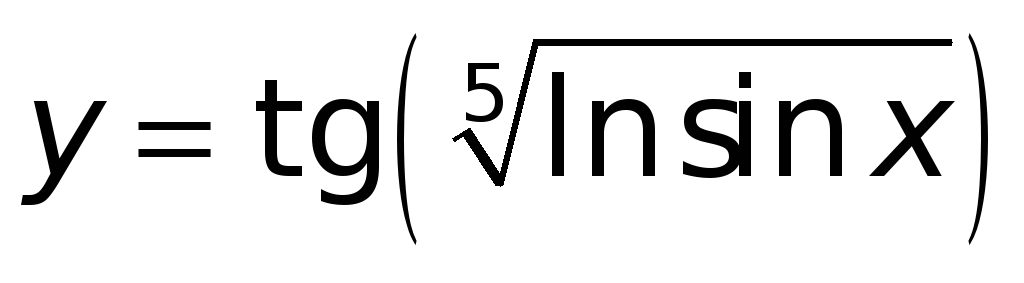 ;
; -
если
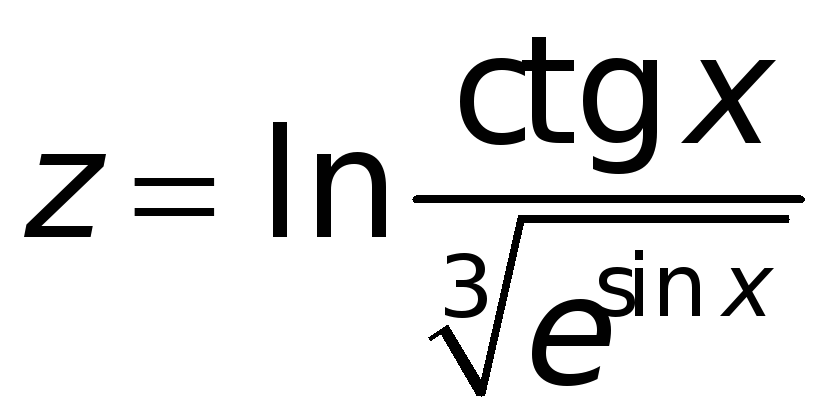 ,
то
,
то
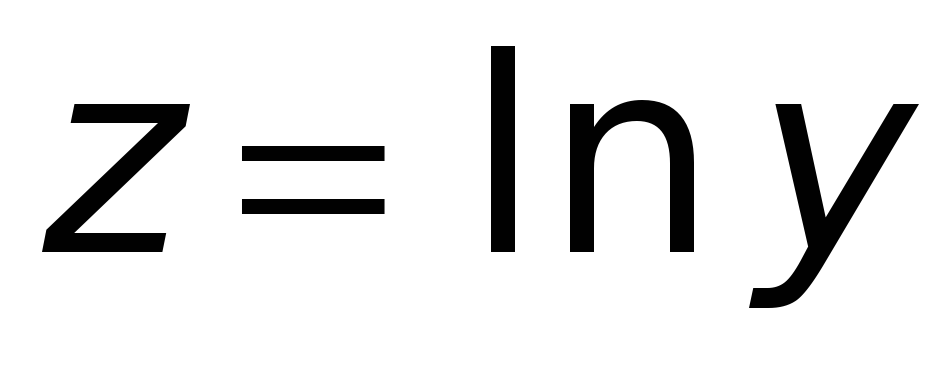 ,
где
,
где
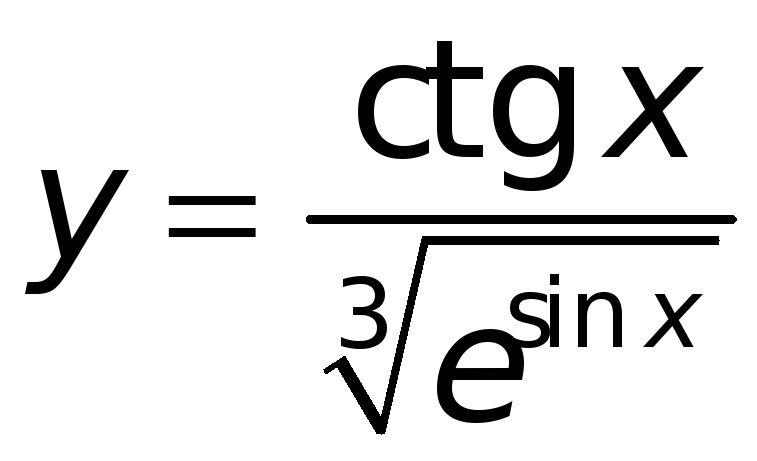 ;
; -
если
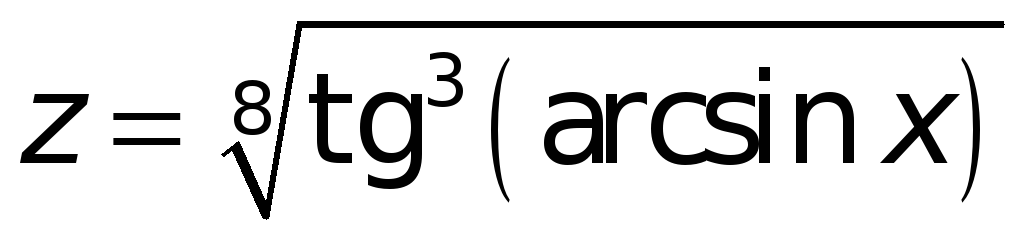 ,
то
,
то
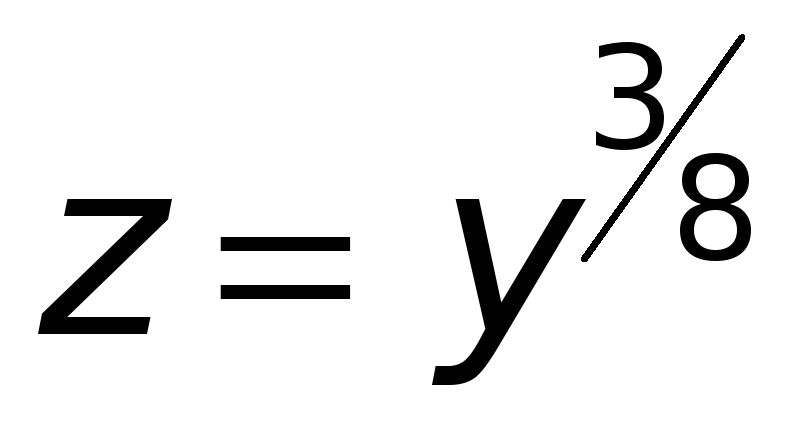 ,
где
,
где
 .
.
Пример.
1) Пусть
![]() ,
тогда
,
тогда
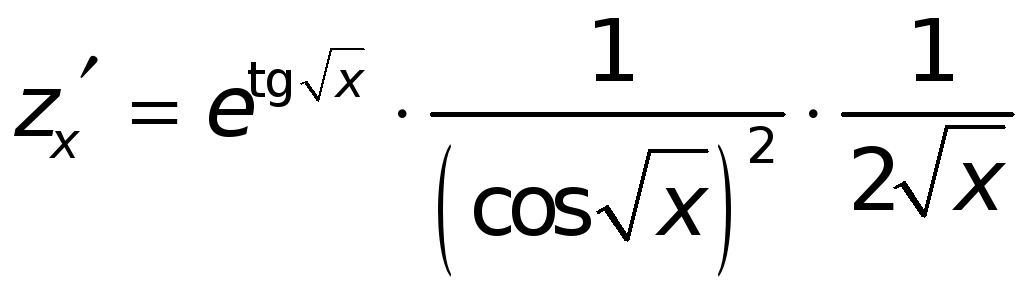 .
.
14. Правила дифференцирования обратных функций.
Пусть функция
![]() определена в промежутке
определена в промежутке
![]() и является там строго монотонной и
непрерывной. Было показано ранее, что
тогда у функции
и является там строго монотонной и
непрерывной. Было показано ранее, что
тогда у функции
![]() имеется обратная функция
имеется обратная функция
![]() ,
определенная в промежутке
,
определенная в промежутке
![]() ,
причем эта функция в промежутке
,
причем эта функция в промежутке
![]() также строго монотонная и непрерывная.
(Здесь
также строго монотонная и непрерывная.
(Здесь
![]() есть множество значений, принимаемых
функцией
есть множество значений, принимаемых
функцией
![]() на промежутке
на промежутке
![]() ).
Пусть у функции
).
Пусть у функции
![]() в точке
в точке
![]() существует конечная отличная от нуля
производная
существует конечная отличная от нуля
производная
![]()
![]() .
Покажем, что тогда у функции
.
Покажем, что тогда у функции
![]() в соответствующей точке
в соответствующей точке
![]()
![]() также существует конечная производная,
причем
также существует конечная производная,
причем
 (короче:
(короче:
![]() ).
).
► Дадим
![]() приращение
приращение
![]() — любое, но такое, что
— любое, но такое, что
![]() и точка
и точка
![]() .
Тогда функция
.
Тогда функция
![]() получит приращение
получит приращение
![]() .
.
Отметим, что в силу
строгой монотонности функции
![]()
![]() ,
если
,
если
![]() .
.
Отметим далее, что
в силу непрерывности функции
![]()
![]() ,
если
,
если
![]() .
.
Имеем очевидное
равенство
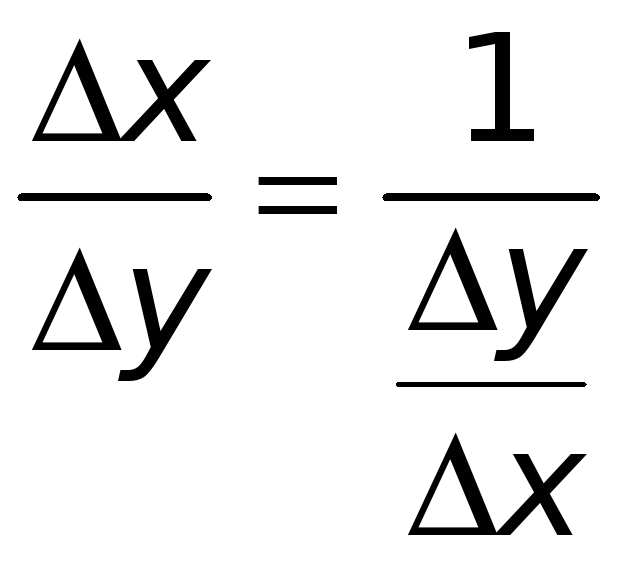 .
Перейдем в этом равенстве к пределу при
.
Перейдем в этом равенстве к пределу при
![]() .
Получим
.
Получим
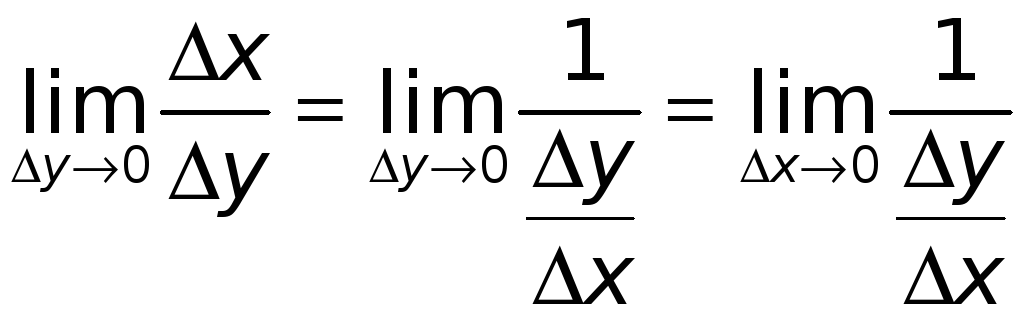 .
.
По условию
![]() — существует конечный, отличный от
нуля. Но тогда существует конечный
— существует конечный, отличный от
нуля. Но тогда существует конечный
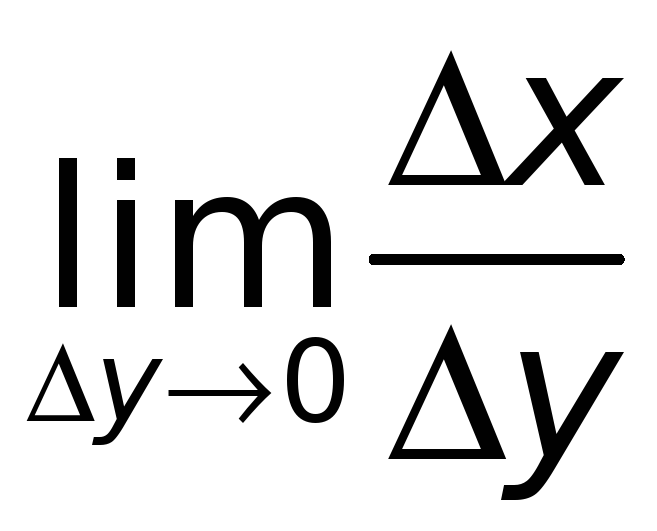 ,
т. е. существует
,
т. е. существует
![]() ,
причем
,
причем
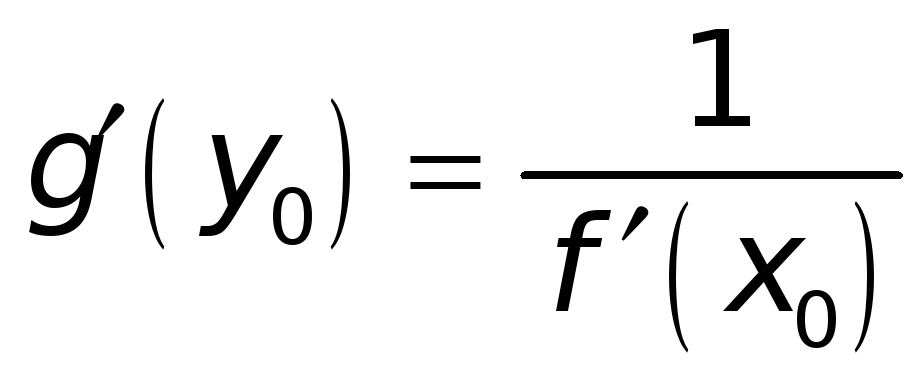 .
◄
.
◄
Итак, производные взаимно-обратных функций есть величины взаимно-обратные.
Исходя из этого, можно получить формулы для производных обратных тригонометрических функций.
15.
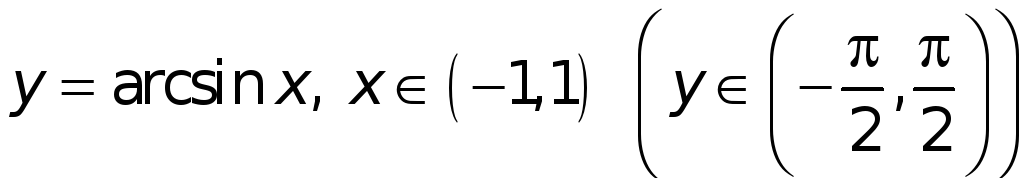 .
.
► Эта функция
является обратной для функции
![]() ,
которая для
,
которая для
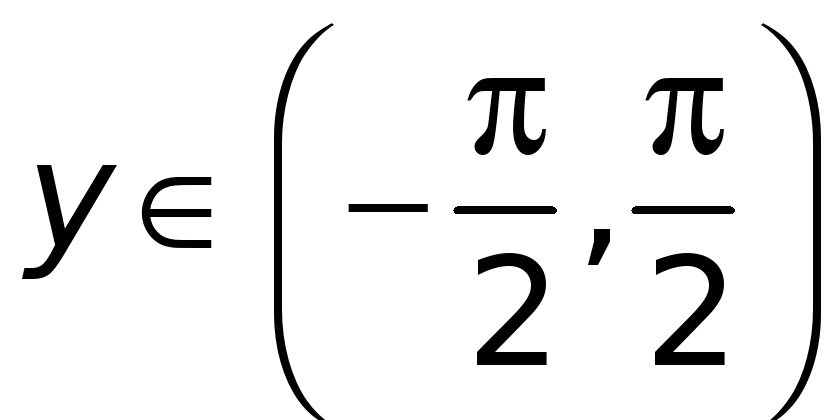 имеет конечную отличную от нуля
производную
имеет конечную отличную от нуля
производную
![]() .
Но тогда функция
.
Но тогда функция
![]() для
для
![]() имеет конечную производную, причем
имеет конечную производную, причем
 .
Перед радикалом взят знак «+», ибо
.
Перед радикалом взят знак «+», ибо
![]() для
для
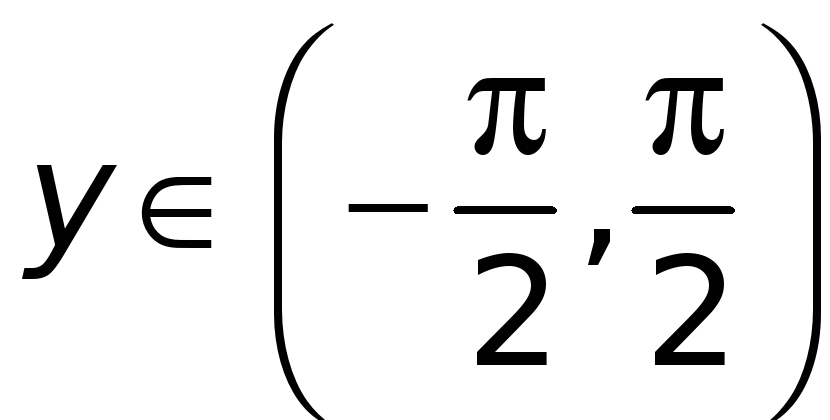 .
Так как
.
Так как
![]() ,
то получаем окончательно
,
то получаем окончательно
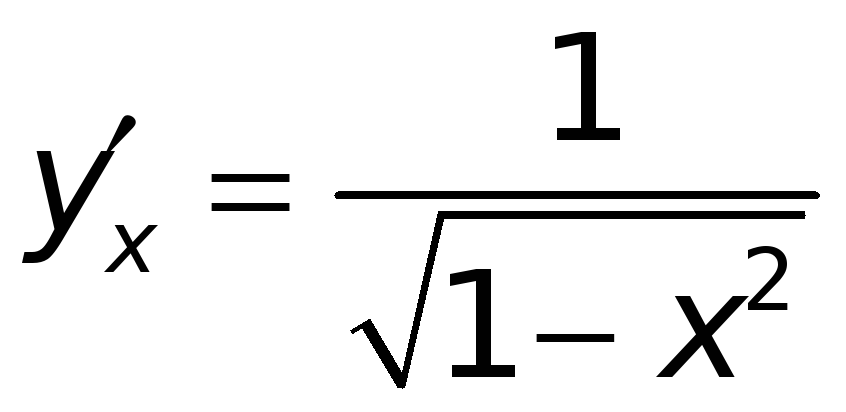 ,
т. е.
,
т. е.
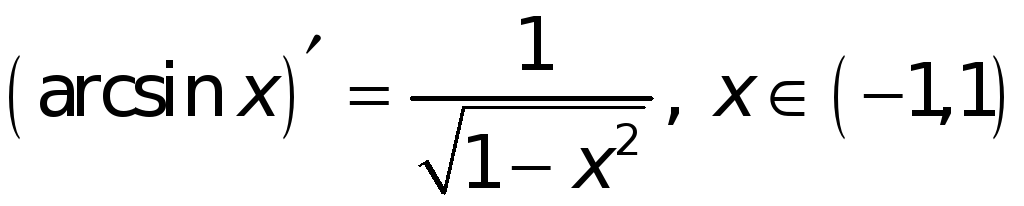
Отметим, что
значения
![]() были исключены, т. к. для соответствующих
значений
были исключены, т. к. для соответствующих
значений
![]() :
:
![]() .
◄
.
◄
16.
![]() .
.
► Эта функция
является обратной для функции
![]() ,
которая для
,
которая для
![]() имеет конечную отличную от нуля
производную
имеет конечную отличную от нуля
производную
![]() .
Но тогда функция
.
Но тогда функция
![]() для
для
![]() имеет конечную производную, причем
имеет конечную производную, причем
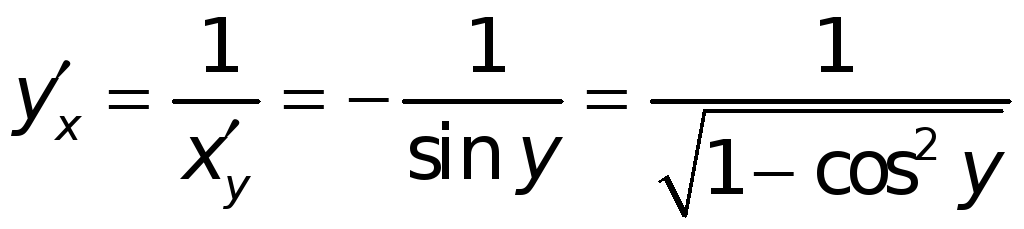 .
Перед радикалом взят знак «+», ибо
.
Перед радикалом взят знак «+», ибо
![]() для
для
![]() .
Так как
.
Так как
![]() ,
то получаем окончательно
,
то получаем окончательно
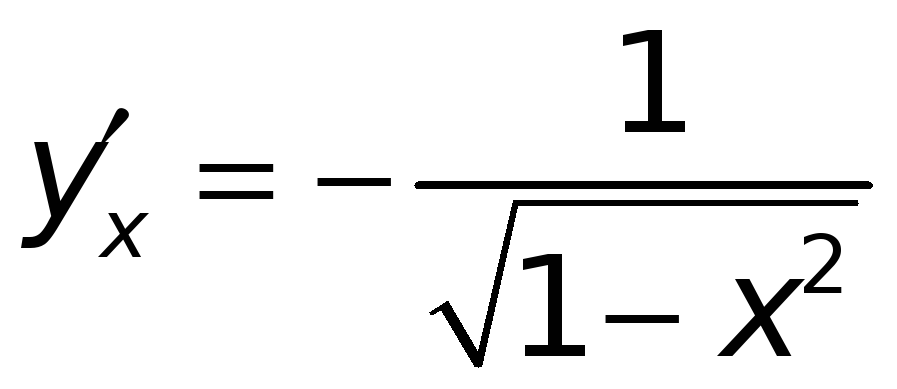 ,
т. е.
,
т. е.

И здесь значения
![]() были исключены, т. к. для соответствующих
значений
были исключены, т. к. для соответствующих
значений
![]() и
и
![]() :
:
![]() .
◄
.
◄
17.
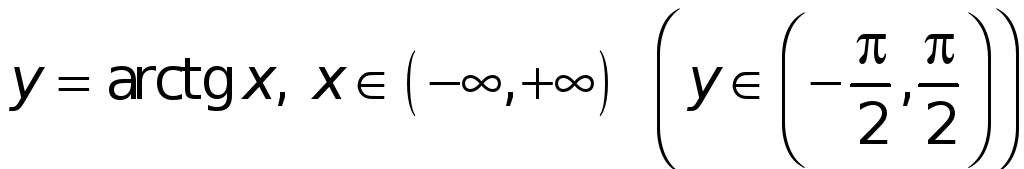 .
.
► Эта функция
является обратной для функции
![]() ,
которая для
,
которая для
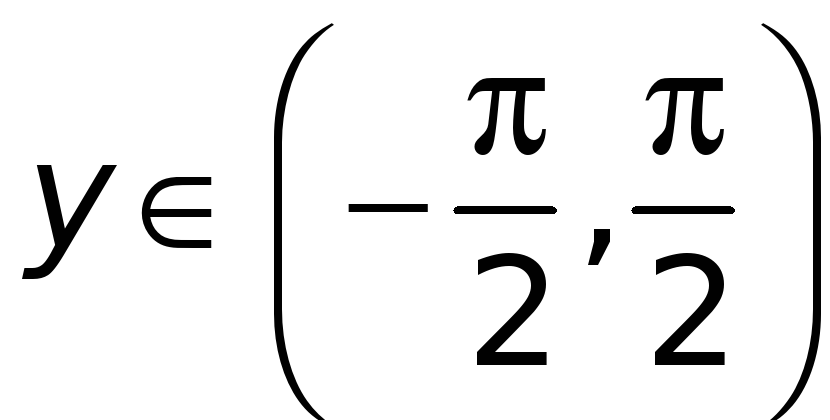 имеет конечную отличную от нуля
производную
имеет конечную отличную от нуля
производную
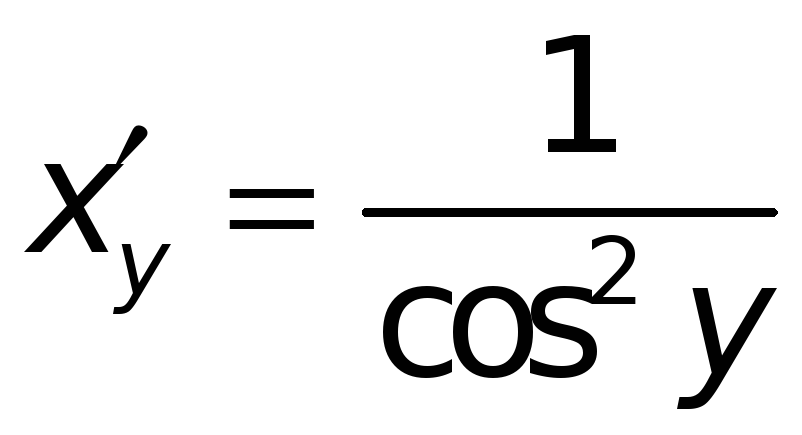 .
Но тогда функция
.
Но тогда функция
![]() для
для
![]() имеет конечную производную, причем
имеет конечную производную, причем
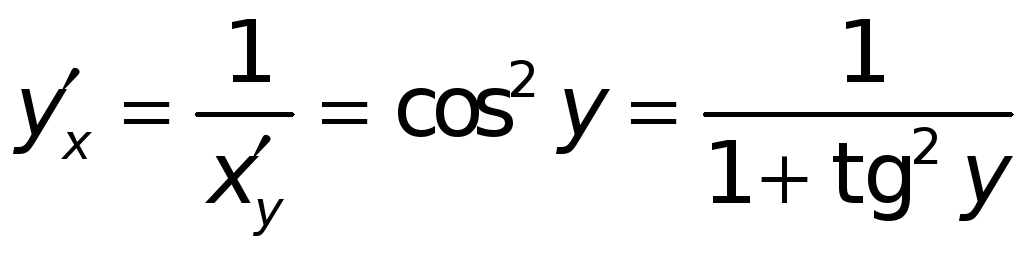 .
Так как
.
Так как
![]() ,
то получаем окончательно
,
то получаем окончательно
![]() ,
т. е.
,
т. е.
![]() ◄
◄
18.
![]() .
.
► Эта функция
является обратной для функции
![]() ,
которая для
,
которая для
![]() имеет конечную отличную от нуля
производную
имеет конечную отличную от нуля
производную
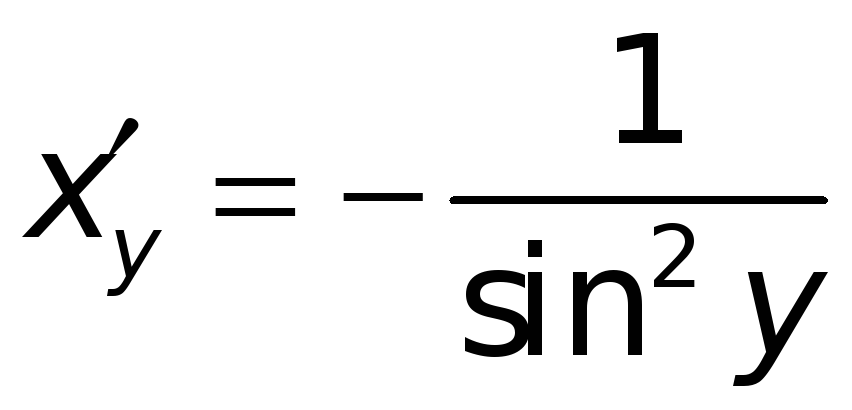 .
Но тогда функция
.
Но тогда функция
![]() для
для
![]() имеет конечную производную, причем
имеет конечную производную, причем
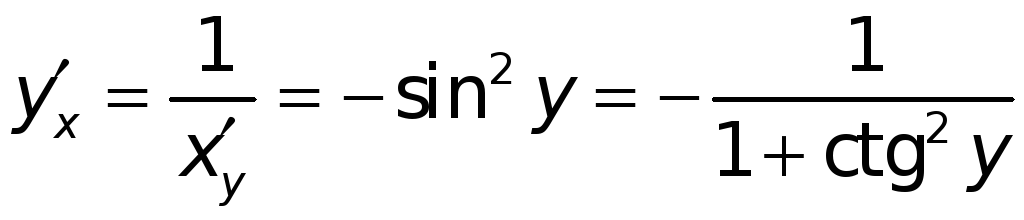 .
Так как
.
Так как
![]() ,
то получаем окончательно
,
то получаем окончательно
![]() ,
т. е.
,
т. е.
![]() ◄
◄
