2. Исследование стационарных критических точек функции с помощью второй производной.

Определение. Пусть функция определена на промежутке и точка является внутренней точкой этого промежутка. Точка называется стационарной критической точкой функции , если .

Лемма. Пусть функция определена на промежутке всюду, за исключением, быть может, точки . Пусть существует конечный, отличный от нуля, предел

.

Тогда существует проколотая -окрестность точки такая, что и для всех , причем значения в имеют знак числа А.

► По условию . Пусть для определенности . Так как , то любому (в частности, ) отвечает число такое, что для всех будет

(считаем число столь малым, что ). Следовательно, для всех будет . В частности, , если . ◄

Теорема 3. Пусть функция определена и непрерывна в промежутке . Пусть точка и является стационарной критической для . Пусть имеет в точке конечную, отличную от нуля, вторую производную (тем самым предполагается, что имеет конечную первую производную не только в точке , но и в некоторой -окрестности точки ). Тогда:

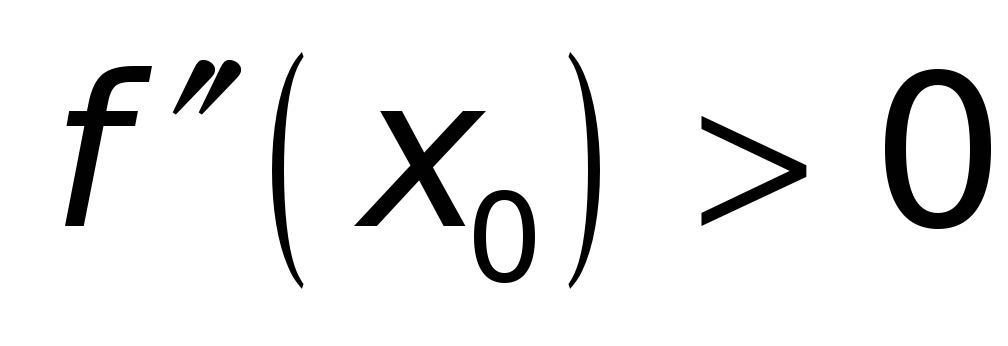1. если , то функция 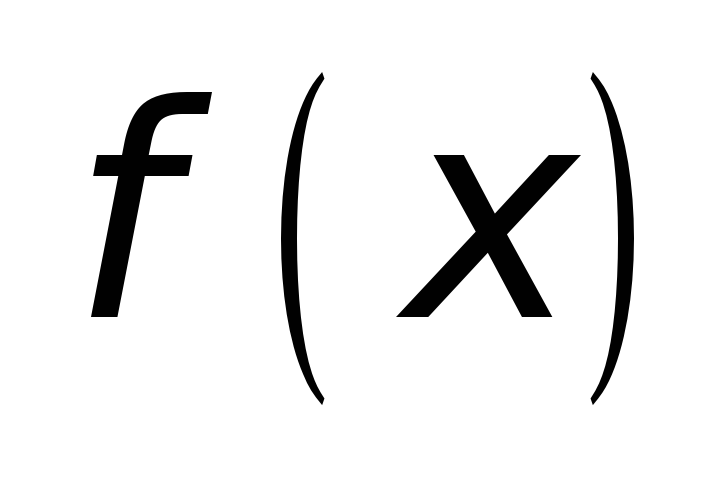имеет в точке 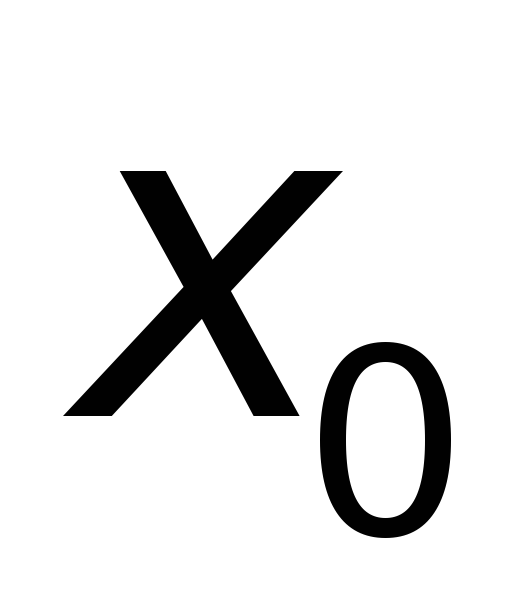строгий минимум;

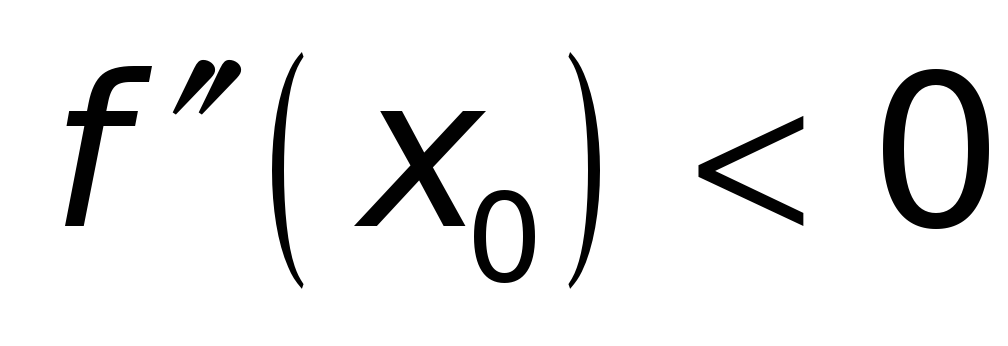2. если , то функция 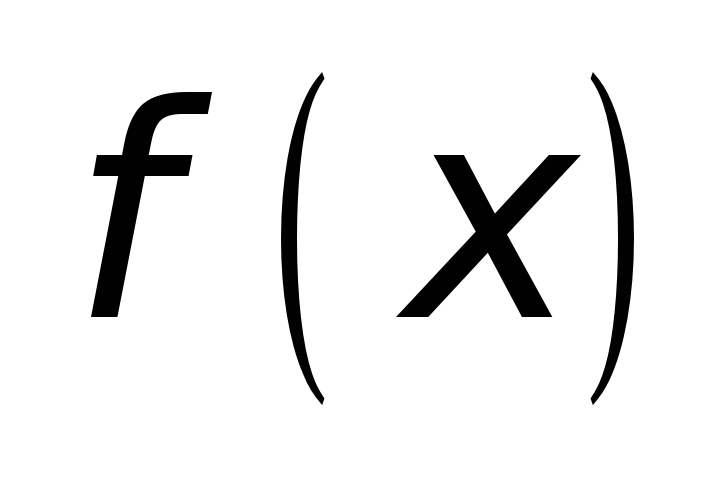имеет в точке 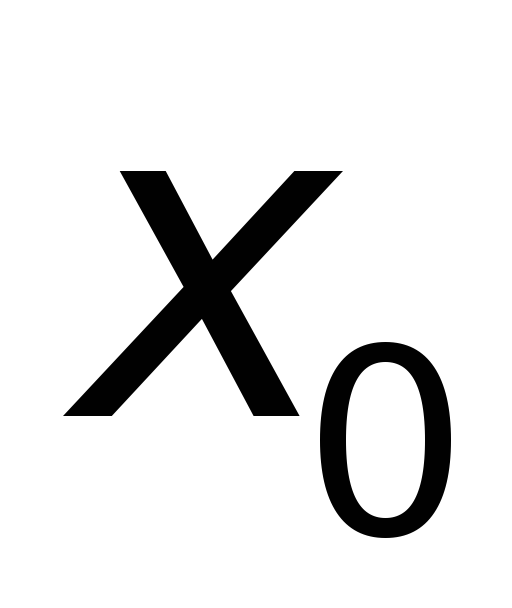строгий максимум.

► Докажем утверждение 1). Утверждение 2) доказывается аналогично. Итак, дано: . Требуется доказать, что имеет в точке строгий минимум. Имеем, по определению,

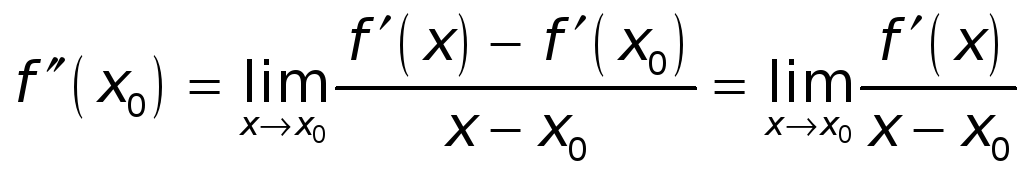
(ибо ). По условию , т. e. 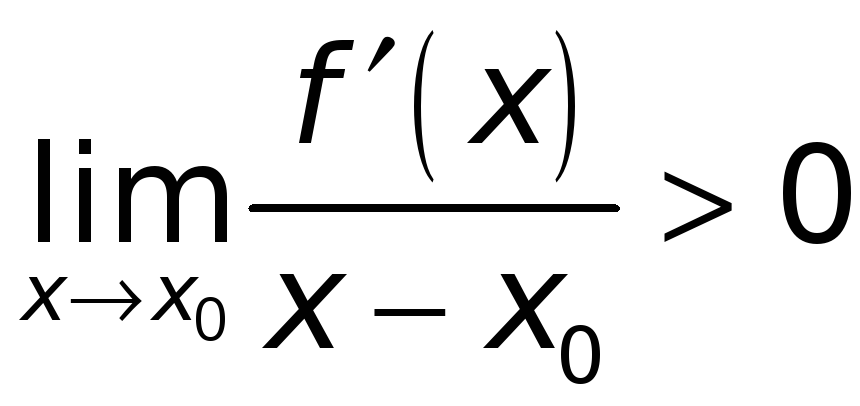. Но тогда, по лемме, существует (можно считать, что ) такая, что будет

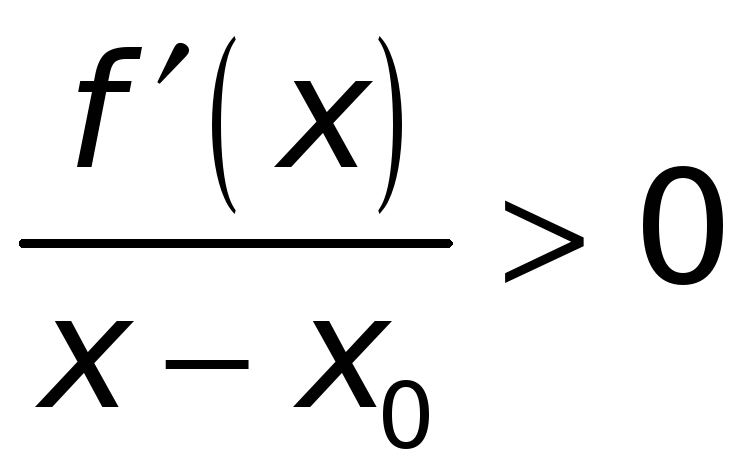для всех . (*)

Возьмем любое . Но тогда и, следовательно, из соотношения (*) следует, что .

Возьмем любое . Но тогда и, следовательно, из соотношения (*) следует, что .

Таким образом, получили: для и для , т. е. что при переходе через точку производная меняет знак с «–» на «+». Это означает, что функция имеет в точке строгий минимум. ◄

Замечание. Если и , то на вопрос: имеет в точке экстремум или нет, теорема 3 ответа не дает. Заметим, что при выполнении условий: , возможны случаи наличия экстремума у функции в точке и случаи его отсутствия (см. рис. 4.22).

Рис. 4.22.

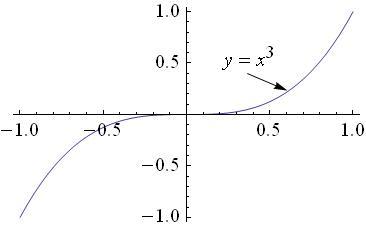
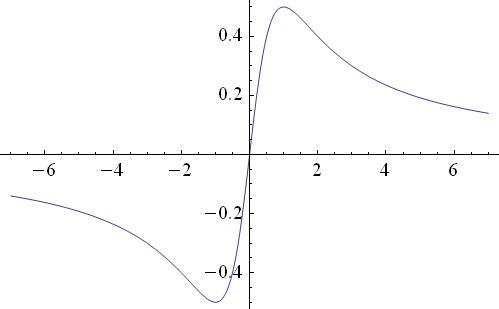
Действительно, для функции в точке обращаются в нуль и . Функция в точке экстремума не имеет.

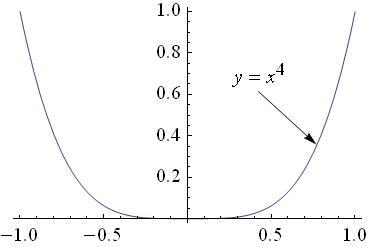
Для функции в точке обращаются в нуль и . Функция в точке имеет минимум.

Рассмотрим пример на применение теоремы 3.

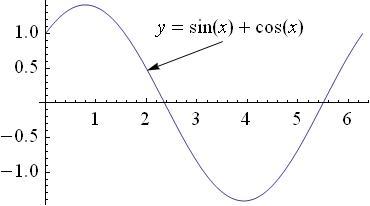
Пример. Исследовать на экстремум функцию в промежутке .

Рис. 4.23.

► Имеем . в точках , . В остальных точках промежутка существует конечная, отличная от нуля. Точки и — стационарные критические точки функции . Имеем , .

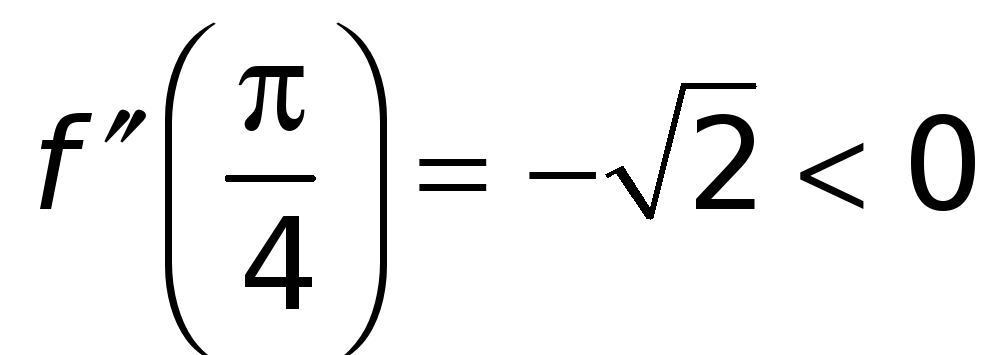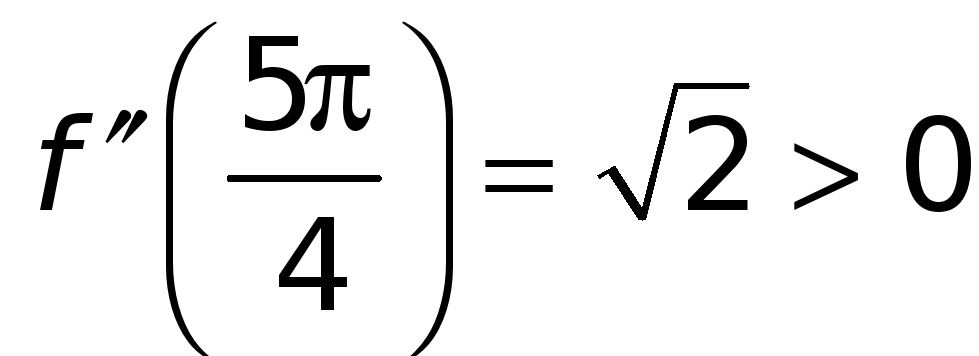Вывод: функция в точке имеет строгий максимум, а в точке — строгий минимум.

§ 13. Характер выпуклости кривой. Точки перегиба

1. Пусть кривая (L) является графиком функции . Пусть точка х₀ — внутренняя точка промежутка , т. е. . Пусть функция имеет в точке х₀ конечную производную , а значит, кривая (L) имеет в точке касательную (К), не параллельную оси .

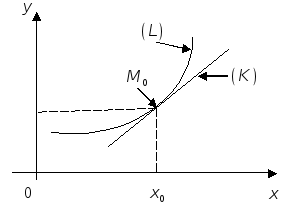
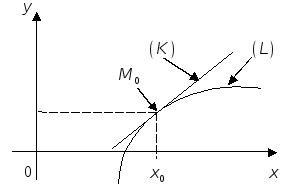
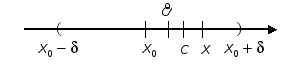
Определение 1. Если существует -окрестность точки х₀ такая, что и для всех оказывается, что точки кривой (L) лежат выше касательной (К) к кривой (L) в точке , то говорят, что (L) в точке направлена выпуклостью вниз (см. рис. 4.24).

Рис. 4.24.	Рис. 4.25.

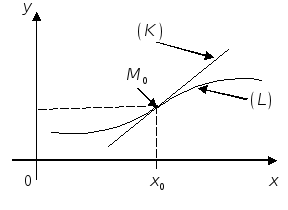
Определение 2. Если существует -окрестность точки х₀ такая, что и для всех оказывается, что точки кривой (L) лежат ниже касательной (К) к кривой (L) в точке , то говорят, что (L) в точке направлена выпуклостью вверх (см. рис. 4.25).

Теорема 1. Пусть (L) есть график функции . Пусть точка х₀ — внутренняя точка промежутка , т. е. . Пусть функция в точке х₀ имеет конечную вторую производную (тем самым предполагается, что имеет конечную первую производную в некоторой -окрестности точки х₀). Тогда:

1) если , то (L) в точке направлена выпуклостью вниз;

2) если , то (L) в точке направлена выпуклостью вверх.

► Докажем утверждение 1). Утверждение 2) доказывается аналогично.

По условию . Это означает, что .

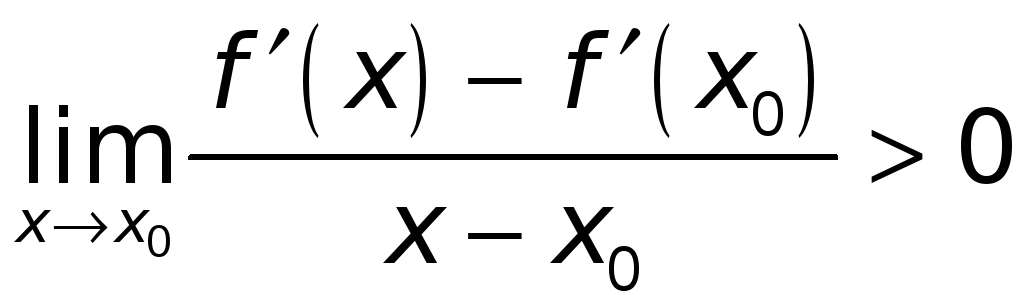Следовательно, существует -окрестность такая, что и для всех будет

. (*)

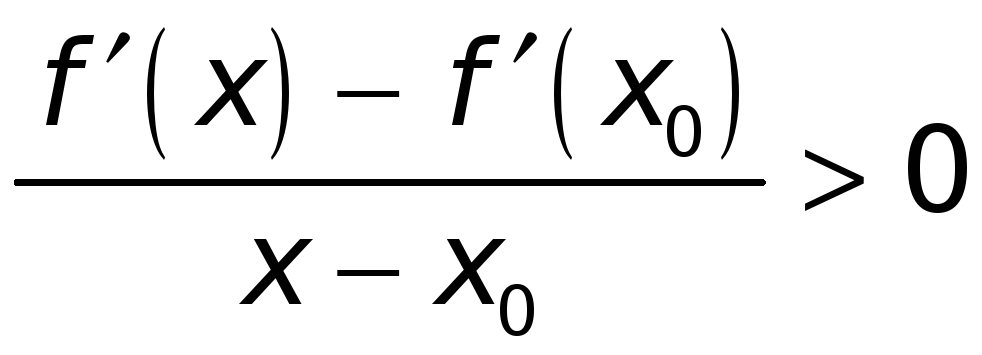Из соотношения (*) следует, что

l) , если ;	(1)
2) , если .

Напишем уравнение касательной (К) к кривой (L) в точке :

. (2)

Станем сравнивать ординаты точек, лежащих на (L) и на (К), при одном и том же х из , т. е. рассмотрим разность . Будем иметь

, . (3)

По теореме Лагранжа , где точка с — некоторая точка, лежащая между точками х₀ и х. А тогда из (3)

. (4)

Возьмем любое . Тогда точка и, следовательно, (см. соотношения (1)). Кроме того, в этом случае . А тогда из соотношения (4) заключаем, что

, т.е. , для . (5)

Возьмем теперь любое . Тогда точка и, следовательно, (см. соотношения (1)). Кроме того, в этом случае . А тогда из соотношения (4) заключаем, что

, т.е. , для . (6)

Из соотношений (5) и (6) следует, что

для любого ,

т.е. что точки кривой (L) лежат выше касательной (К) к (L) в точке для всех . Значит, кривая (L) в точке М₀ направлена выпуклостью вниз. ◄

2. точки перегиба. Пусть (L) является графиком функции . Пусть точка х₀ — внутренняя точка промежутка , т. е. . Пусть кривая (L) имеет в точке касательную (К), не параллельную оси .

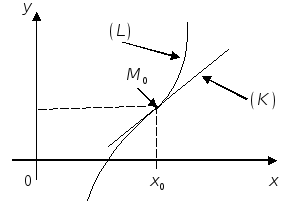
Определение. Если существует -окрестность точки такая, что и оказывается что: для всех точки кривой (L) лежат по одну сторону от касательной (К) к кривой (L) в точке , а для всех точки кривой (L) лежат по другую сторону от касательной (К) к кривой (L) в точке , то точка называется точкой перегиба кривой (L) (рис. 4.26).

рис. 4.26.

Из теоремы, доказанной выше, следует, что точки перегиба кривой (L) следует искать среди точек, в которых либо , либо , либо не существует. Следует заметить, что не в каждой точке, в которой имеет место одно из этих трех соотношений, кривая (L) имеет перегиб. Так, например, для функции , имеем . Однако точка не является точкой перегиба графика (L) этой функции, ибо все точки кривой (L) лежат выше касательной (К) к этой кривой в точке (см. рис. 4.22).

Точки, в которых либо , либо не существует, либо , будем называть точками, подозрительными на перегиб.

Теорема 2. Пусть (L) есть график функции , . Пусть точка и пусть кривая (L) имеет в точке касательную (К), не параллельную оси . Пусть точка является подозрительной на перегиб. Пусть имеется -окрестность точки такая, что и для любого существует конечная , причем сохраняет знак как в , так и в (в каждой полуокрестности сохраняет свой знак). Тогда:

1) если при переходе через точку х₀ вторая производная меняет знак, то кривая (L) в точке имеет перегиб;

2) если при переходе через точку х₀ вторая производная не меняет знак, то у кривой (L) в точке перегиба нет.

► Напишем уравнение касательной (К) к кривой (L) в точке :

.

Возьмем затем любую точку и сравним при этом х ординаты точек, лежащих на (L) и на (К). Для этого рассмотрим разность . Имеем

.

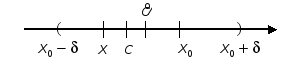
По теореме Лагранжа , где точка — некоторая точка, лежащая между точками х₀ и х (см. рис. 4.27). Следовательно,

. (7)

Рис. 4.27.

Из условия теоремы следует, что определена и непрерывна в промежутке и что существует конечная, по крайней мере, в промежутке . Видим, что функция удовлетворяет условиям теоремы Лагранжа в промежутке . Следовательно, , где — некоторая точка, лежащая между точками с и х₀.

Теперь вместо (7) можем написать

. (8)

Заметим, что если , то и ; если , то и . Значит, в обоих случаях: . А тогда из (8) заключаем, что знак разности определяется знаком .

Рассмотрим случай I, когда при переходе через точку х₀ меняет знак. Пусть, для определенности, для и для .

Было замечено выше, что если , то и , а значит, (у нас, по условию, для любого ). Следовательно, для любого , т. е.

, для любого . (9)

Было замечено выше, что если , то и , а значит, (у нас, по условию, для любого ). Получаем, следовательно, для любого , т.е.

, для любого . (10)

Из (9) и (10) видим, что для всех точки кривой (L) лежат ниже касательной (К) к кривой (L) в точке , а для всех точки кривой (L) лежат выше этой касательной. Значит, точка есть точка перегиба кривой (L).

Рассмотрим случай II, когда не меняет знак при переходе через точку х₀. Пусть, для определенности, как для , так и для .

Пусть х — любое из . Тогда и . Значит, (у нас, по условию, , для любого ). Следовательно, =>

, для любого . (11)

Возьмем х — любое из . Тогда и . Значит, (у нас, по условию, , для любого ). Следовательно, =>

, для любого . (12)

Из (11) и (12) видим, что для всех , т. е. что для всех точки кривой (L) лежат ниже касательной (К) к кривой (L) в точке . Значит, кривая (L) в точке не имеет перегиба. ◄

Пример. Найти точки экстремума, точки перегиба и исследовать характер выпуклости кривой, заданной уравнением , .

► Имеем 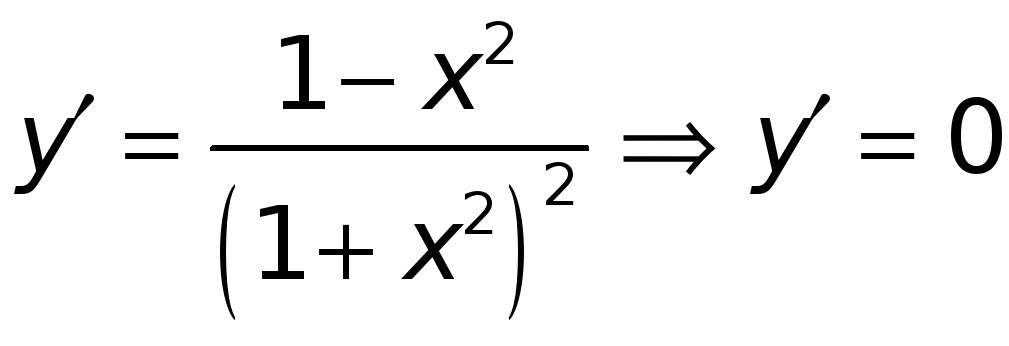в точках и . Во всех остальных точках промежутка существует конечная, отличная от нуля. Имеем, далее 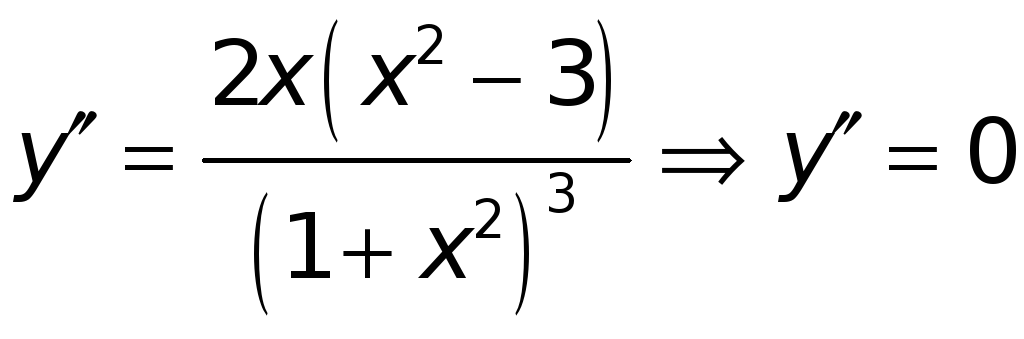в точках , и . Во всех остальных точках промежутка существует конечная, отличная от нуля.

Вывод:

1) Точки и — подозрительны на гладкий экстремум.

2) Точки , и — подозрительны на перегиб. Имеем:

точка есть точка строгого минимума; .

точка есть точка строгого максимума; .

При переходе через точку вторая производная меняет знак с «–» на «+». Значит, точка 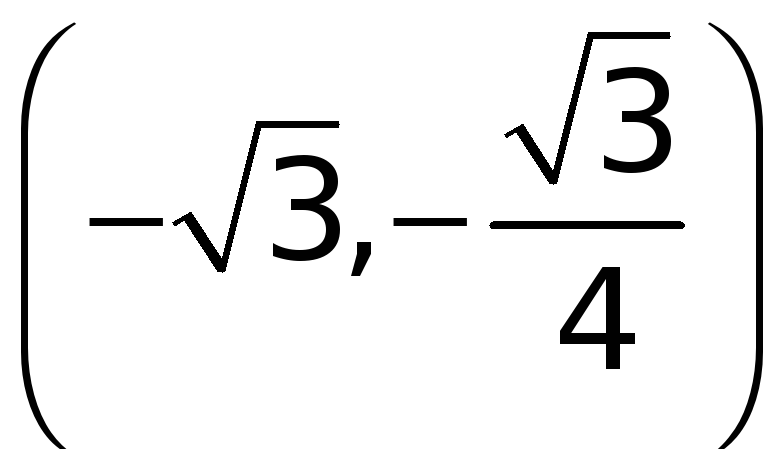есть точка перегиба графика функции .

При переходе через точку вторая производная меняет знак с «+» на «–». Значит, точка (0, 0) есть точка перегиба графика функции .

При переходе через точку вторая производная меняет знак с «–» на «+».Значит, точка 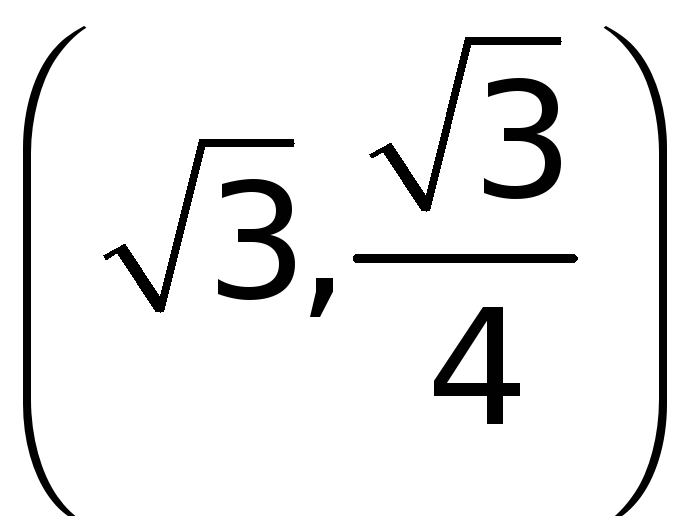есть точка перегиба графика функции .

Для : (выпуклость вверх).

Для : (выпуклость вниз).

Для : (выпуклость вверх).

Для : (выпуклость вниз).

Имеем

На рис. 4.28 представлена схема графика функции .

Рис. 4.28.

Замечание. Пусть кривая (L) является графиком функции , . Из изложенного выше приходим к выводу, что точками перегиба кривой (L) оказываются точки, при переходе через которые изменяется направление выпуклости (L). В определении точки , как точки перегиба кривой (L), предполагалось, что что кривая (L) в точке имеет касательную, не параллельную оси . Если исходить из определения точки перегиба кривой (L), как точки, при переходе через которую изменяется направление выпуклости кривой, то можно отказаться от этого ограничения. Тогда точками перегиба кривой (L) будут также точки, в которых производная бесконечна, но определенного знака.

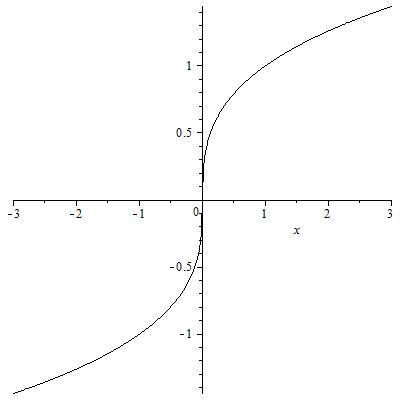
Так, например, для кривой (L), являющейся графиком функции , , точка М₀ (0, 0) будет точкой перегиба (см. рис. 4.29).

Рис. 4.29.	Рис. 4.30.

И, вообще, следует отметить, что точки графика функции , , для которых либо , либо , но в которых нет экстремума, будут точками перегиба. Это утверждение справедливо лишь в случае, когда указанные критические точки функции являются изолированными, т. е. когда существует окрестность каждой такой точки, в которой нет других критических точек функции .

Рассмотрим еще один пример. Пусть кривая (L) является графиком функции , . Имеем , но в точке х = 0 эта функция не имеет экстремума. Точка М₀ (0, 0) будет точкой перегиба графика функции (см. рис. 4.30).