2. Формула Лейбница для производной n-го порядка от произведения двух функций.

Теорема. Пусть функции и в некотором промежутке имеют конечные производные всех порядков до включительно. Тогда функция имеет в промежутке конечные производные всех порядков до включительно, причем

. (*)

► Имеем (это известно);

.

Допустим, что формула (*) верна для любого , удовлетворяющего условию: . Тогда

.

Так как

,

,

……………………………….

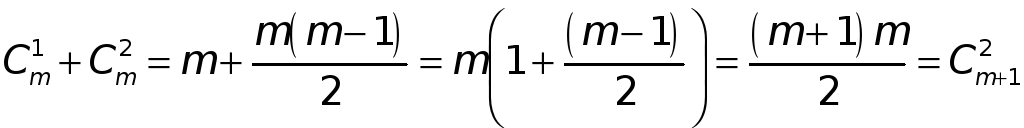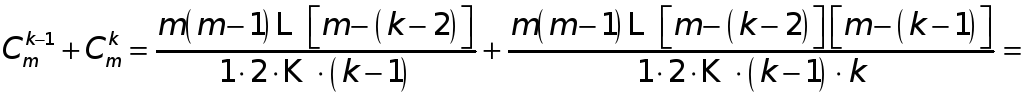
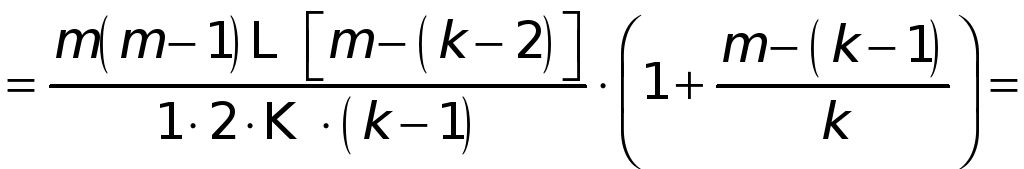
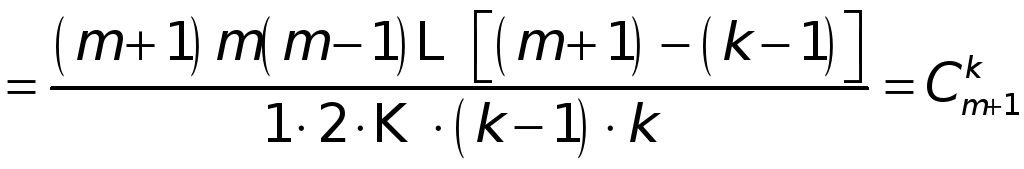
то получаем

.

Видим, что переход от к сделан. Для формула (*) установлена непосредственно. В силу перехода от к формула (*) будет верна для . ◄

Замечание. Формула Лейбница, которую мы сейчас установили, во многих случаях позволяет сократить вычисления.

Пример. Пусть . Требуется вычислить .

► Имеем

. ◄

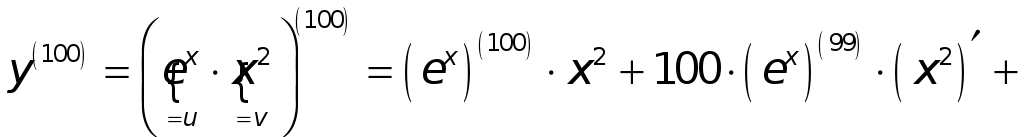
3. Механическое истолкование второй производной.

Пусть материальная точка М движется по прямой линии по закону . Мы знаем, что скорость точки М в момент времени t равна: . Поставим себе задачу: найти ускорение точки М в данный момент времени t.

Для этого перейдем от момента времени t к моменту . За промежуток времени от до скорость точки М получит приращение . Среднее ускорение точки М за промежуток времени от до будет равно: .

Легко понять, что чем меньше промежуток времени , тем меньше будет отличаться от ускорения точки М в момент t. Исходя из этого, ускорением точки М в момент t будем называть предел, к которому стремится среднее ускорение , когда .

Таким образом, ускорение точки М в момент времени t определяется равенством или

.

Итак, ускорение точки , движущейся по прямой, в момент есть вторая производная от функции, описывающей закон движения точки М, вычисленная в момент t.

§ 6. Дифференциалы высших порядков

Пусть функция определена в некотором промежутке Х и имеет там конечную производную . Тогда, как мы знаем,

. (1)

Ясно, что есть функция от х, определенная в промежутке X, и поэтому можно поставить вопрос о нахождении дифференциала от этой новой функции.

Второй дифференциал функции определяется как дифференциал от первого дифференциала, т. е. . Если дифференциал порядка () функции уже определен, то дифференциал порядка функции равен: .

При этом, конечно, предполагается существование соответствующих дифференциалов.

При вычислении дифференциалов высшего порядка следует существенно различать два случая: 1) когда аргумент х является независимой переменной; 2) когда аргумент х представляет собой дифференцируемую функцию некоторой переменной t.

Переходя к вычислению дифференциалов высшего порядка, прежде всего рассмотрим случай, когда аргумент х является независимой переменной. В этом случае , т. е. совпадает с произвольным приращением независимой переменной, а значит, не зависит от х и, следовательно, при дифференцировании по х величину следует рассматривать как постоянное число. Стало быть, будем иметь

, (2)

, (3)

Допустим, что

. (*)

Тогда

.

Видим, что переход от к сделан. Для формула (*) установлена непосредственно. В силу перехода от к формула (*) будет верна для , т. е. вплоть до того , для которого существуют соответствующие дифференциалы функции . Из формулы (*) получаем следующее равенство:

.

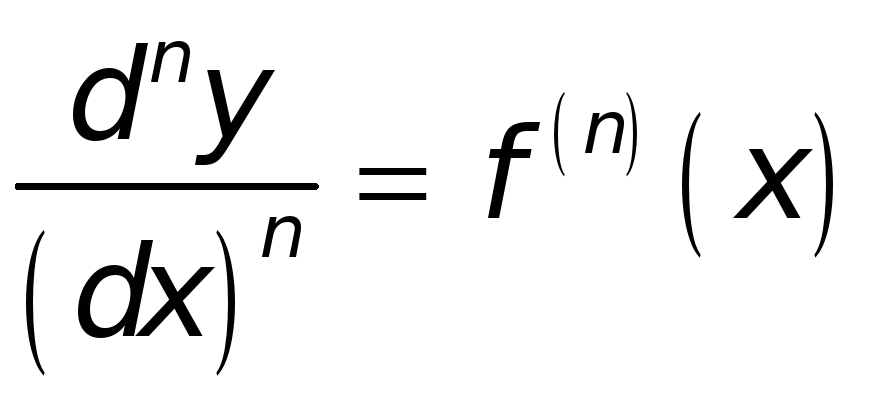Таким образом, для случая, когда аргумент х является независимой переменной, -я производная функции в точке равна отношению дифференциала -го порядка этой функции в точке х, к -й степени дифференциала аргумента.

Перейдем теперь к рассмотрению случая, когда аргумент х сам является функцией некоторой переменной t. Будем иметь в этом случае , где — независимая переменная, а х — промежуточная переменная.

По свойству инвариантности формы дифференциала первого порядка сложной функции и в этом случае будет .

Только в этом случае уже нельзя рассматривать как постоянное число, ибо . Здесь уже второй дифференциал , вообще говоря, не равен нулю и определяется формулой . Поэтому, используя правило вычисления дифференциала от произведения двух функций, будем иметь, например,

. (5)

. (6)

Мы видели, что когда переменная х была независимой, то , (см. формулы (2) и (3)). Сопоставив эти равенства с равенствами (5) и (6) соответственно, замечаем, что свойство инвариантности формы для дифференциалов сложной функции порядка () в общем случае уже не имеет места.

Мы сказали «в общем случае» потому, что имеется частный случай, когда свойство инвариантности имеет место. Это будет тогда, когда х является линейной функцией от t, т. е. ( и — постоянные числа). Действительно, в этом случае , и, следовательно, вместо формул (5) и (6) будем иметь , .