
- •Глава 4 Производная и дифференциал § 1. Производная. Механический и геометрический смысл производной
- •4. Односторонние производные.
- •§2. Понятие дифференцируемости функции
- •§ 3. Формулы и правила вычисления производных
- •7. Простейшие правила вычисления производных.
- •12. Формула для приращения функции.
- •13. Правило дифференцирования сложной функции.
- •14. Правила дифференцирования обратных функций.
- •§ 4. Дифференциал функции
- •2. Геометрический смысл дифференциала.
- •3. Сводка формул для дифференциалов.
- •4. Дифференциал сложной функции. Инвариантность формы дифференциала.
- •§ 5. Производные высших порядков
- •2. Формула Лейбница для производной n-го порядка от произведения двух функций.
- •3. Механическое истолкование второй производной.
- •§ 6. Дифференциалы высших порядков
- •§ 7. Дифференцирование функции, заданной параметрически
- •§ 8. Основные теоремы дифференциального исчисления
- •§ 9. Формула Тейлора
- •2. Примеры разложения по формуле Тейлора.
- •§ 10. Раскрытие неопределенностей по правилу Лопиталя
- •1. Неопределенность вида .
- •2. Неопределенность вида .
- •§ 11. Признаки постоянства, возрастания и убывания функций
- •§ 12. Теория экстремальных значений функции
- •2. Исследование стационарных критических точек функции с помощью второй производной.
- •§ 13. Характер выпуклости кривой. Точки перегиба
- •§ 14. Асимптоты кривой
- •§ 15. Построение графика функции по характерным точкам
§ 4. Дифференциал функции
1. Определение
дифференциала.
Пусть функция
![]() определена в некотором промежутке X
и пусть точка
определена в некотором промежутке X
и пусть точка
![]() .
Дадим значению х0
аргумента приращение
.
Дадим значению х0
аргумента приращение
![]() — любое, но такое, что
— любое, но такое, что
![]() и точка
и точка
![]() .
Пусть
.
Пусть
![]() есть приращение функции
есть приращение функции
![]() в точке х0,
соответствующее приращению
в точке х0,
соответствующее приращению
![]() аргумента. Мы знаем, что если функция
аргумента. Мы знаем, что если функция
![]() имеет в точке х0
конечную производную
имеет в точке х0
конечную производную
![]() ,
то приращение
,
то приращение
![]() функции представимо в виде
функции представимо в виде
![]() ,
(1)
,
(1)
где
![]() .
.
Замечаем, что если
![]() ,
то первое слагаемое в правой части
формулы (1) пропорционально величине
,
то первое слагаемое в правой части
формулы (1) пропорционально величине
![]() или, как говорят, линейно зависит от
или, как говорят, линейно зависит от
![]() .
Так как в этом случае
.
Так как в этом случае
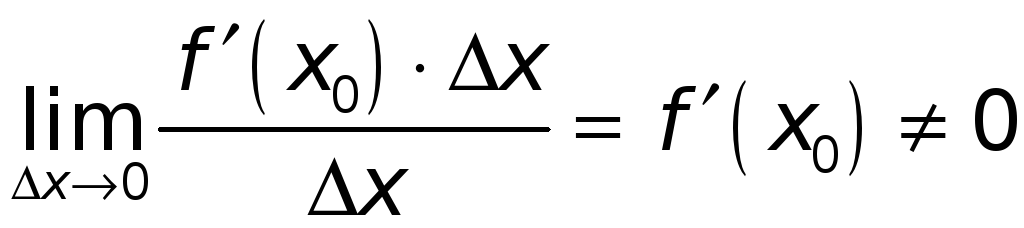 ,
то упомянутое слагаемое
,
то упомянутое слагаемое
![]() является при
является при
![]() бесконечно малой того же порядка, что
и
бесконечно малой того же порядка, что
и
![]() .
.
Второе слагаемое
![]() правой части (1) при
правой части (1) при
![]() является бесконечно малой более высокого
порядка, чем
является бесконечно малой более высокого
порядка, чем
![]() ,
ибо
,
ибо
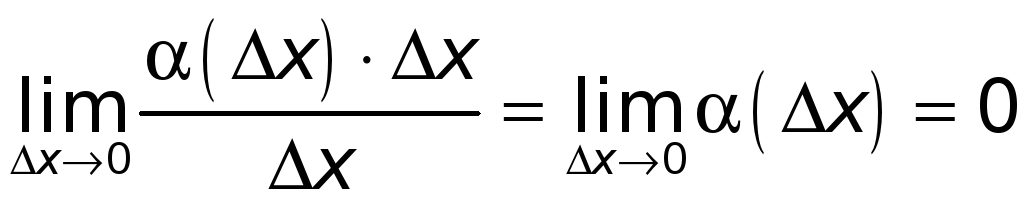 .
.
Полагаем
![]() (2)
(2)
и называем эту
величину дифференциалом
функции
![]() в точке х0.
в точке х0.
Таким образом,
дифференциалом функции
![]() в точке х0
называется произведение производной,
вычисленной в этой точке, на приращение
в точке х0
называется произведение производной,
вычисленной в этой точке, на приращение
![]() независимой переменной.
независимой переменной.
Дифференциалом
независимой переменной х
называют ее приращение, т. е. полагают
![]() .
Следовательно, вместо равенства (2) можно
писать
.
Следовательно, вместо равенства (2) можно
писать
![]() .
(3)
.
(3)
Из равенства (3),
разрешая его относительно
![]() ,
находим
,
находим
![]() .
(4)
.
(4)
Тем самым символ
![]() может рассматриваться как обычная
дробь, знаменатель которой есть
может рассматриваться как обычная
дробь, знаменатель которой есть
![]() ,
а числитель —
,
а числитель —
![]() .
.
Вернемся снова к
формуле (1). Если
![]() ,
т. е.
,
т. е.
![]() при
при
![]() ,
то
,
то
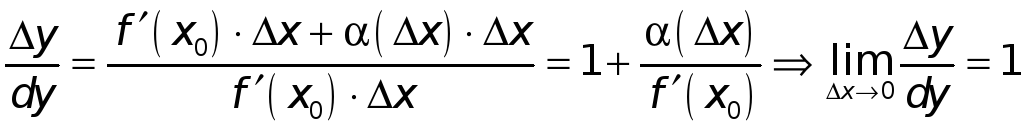 .
.
Значит, в случае,
когда
![]() ,
приращение функции
,
приращение функции
![]() и ее дифференциал
и ее дифференциал
![]() оказываются эквивалентными бесконечно
малыми при
оказываются эквивалентными бесконечно
малыми при
![]() .
Поэтому в этом случае вполне оправдано
приближенное равенство
.
Поэтому в этом случае вполне оправдано
приближенное равенство
![]() .
(5)
.
(5)
Ясно, что приближенное
равенство (5) тем точнее (как в смысле
абсолютной, так и в смысле относительной
погрешности), чем меньше
![]() .
.
Обычно структура
дифференциала функции
![]() значительно проще структуры ее приращения
значительно проще структуры ее приращения
![]() ,
и поэтому формулой (5) широко пользуются
в приближенных вычислениях. Например,
для функции
,
и поэтому формулой (5) широко пользуются
в приближенных вычислениях. Например,
для функции
![]() :
:
![]() ,
,
в то время как
![]() .
.
Если взять
![]() ,
то
,
то
![]() ,
,
а
![]() .
.
Таким образом, абсолютная ошибка
![]() ,
,
относительная ошибка
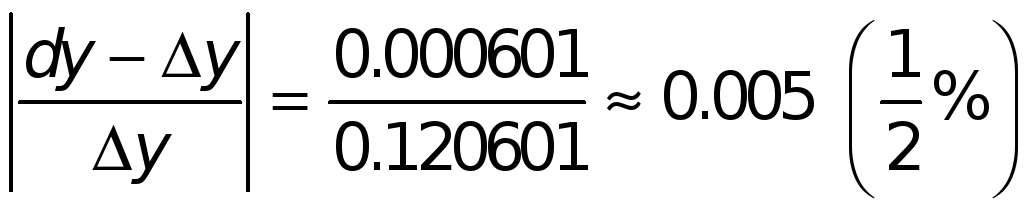 .
.
2. Геометрический смысл дифференциала.
Пусть имеется
график (L)
функции
![]() .
Пусть значению х0
аргумента х
на кривой отвечает некоторая точка М0.
Проведем к кривой (L)
в точке М0
касательную М0Т.
Для углового коэффициента касательной
мы знаем формулу
.
Пусть значению х0
аргумента х
на кривой отвечает некоторая точка М0.
Проведем к кривой (L)
в точке М0
касательную М0Т.
Для углового коэффициента касательной
мы знаем формулу
![]() .
.
При переходе от
![]() к
к
![]() ордината касательной получит приращение
ордината касательной получит приращение
![]() .
.
Таким образом,
![]() есть приращение ординаты точки, лежащей
на касательной к кривой (L)
в точке М0,
при переходе от х0
к
есть приращение ординаты точки, лежащей
на касательной к кривой (L)
в точке М0,
при переходе от х0
к
![]() .
.
Отметим, что замена
приращения функции
![]() дифференциалом
дифференциалом
![]() равносильна переходу от заданной
функциональной зависимости
равносильна переходу от заданной
функциональной зависимости
![]() от х
от х
![]() к линейной зависимости
к линейной зависимости
![]() от х
в достаточно малой окрестности точки
х0.
При такой замене получающаяся погрешность
оказывается бесконечно малой более
высокого порядка, чем приращение
аргумента.
от х
в достаточно малой окрестности точки
х0.
При такой замене получающаяся погрешность
оказывается бесконечно малой более
высокого порядка, чем приращение
аргумента.
3. Сводка формул для дифференциалов.
Поскольку
дифференциал
![]() функции
функции
![]() получается умножением производной этой
функции
получается умножением производной этой
функции
![]() на дифференциал независимой переменной
dx,
постольку операции на вычисление
производной и дифференциала, с точки
зрения техники вычислений, почти не
отличаются друг от друга. Это позволяет
нам из сводки формул для производных
получить соответствующую сводку формул
для дифференциалов.
на дифференциал независимой переменной
dx,
постольку операции на вычисление
производной и дифференциала, с точки
зрения техники вычислений, почти не
отличаются друг от друга. Это позволяет
нам из сводки формул для производных
получить соответствующую сводку формул
для дифференциалов.
Например, из формулы
![]() ,
умножив обе части на dx,
получим
,
умножив обе части на dx,
получим
![]() ,
,
или
![]() .
.
Поступая аналогичным образом и в иных случаях, найдем:
-
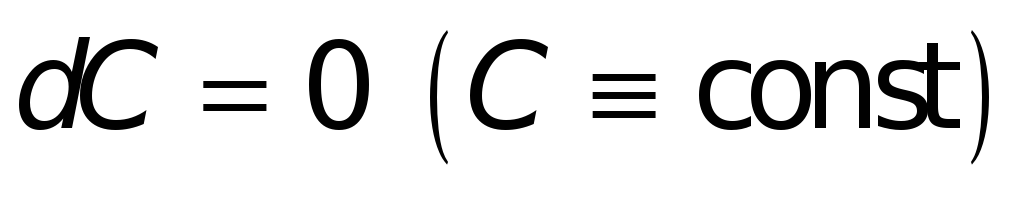 .
. -
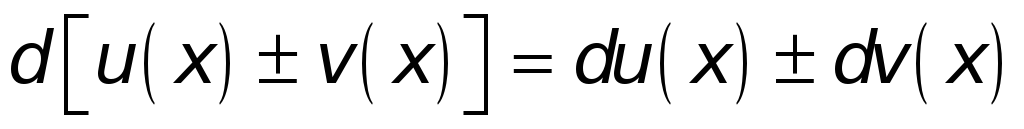 .
. -
 .
. -
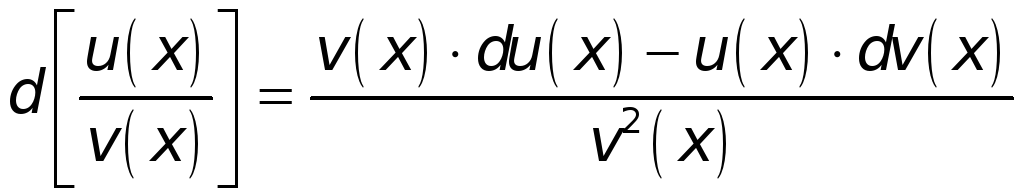 .
. -
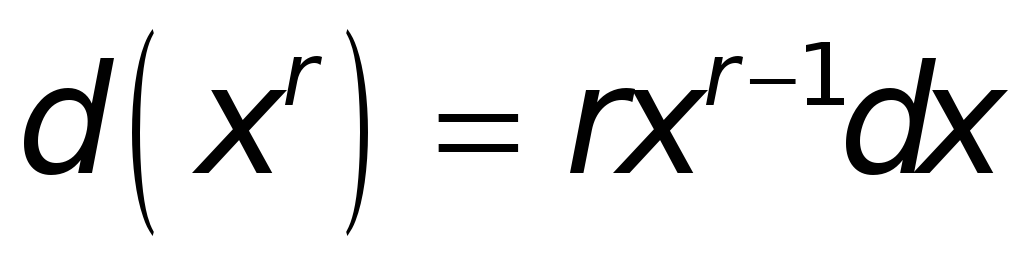 .
. -
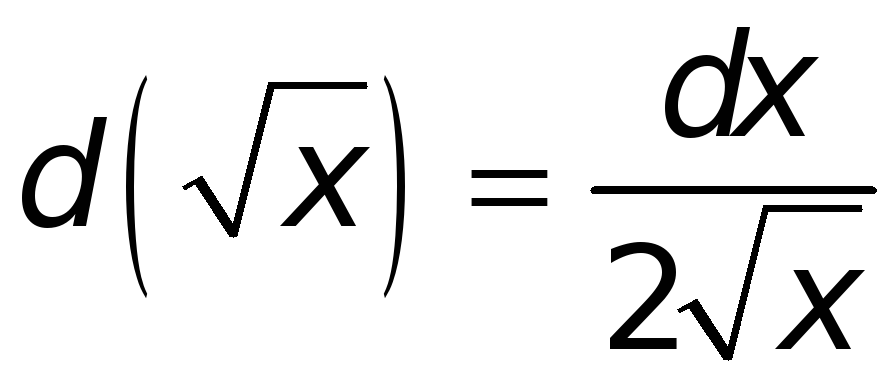 .
. -
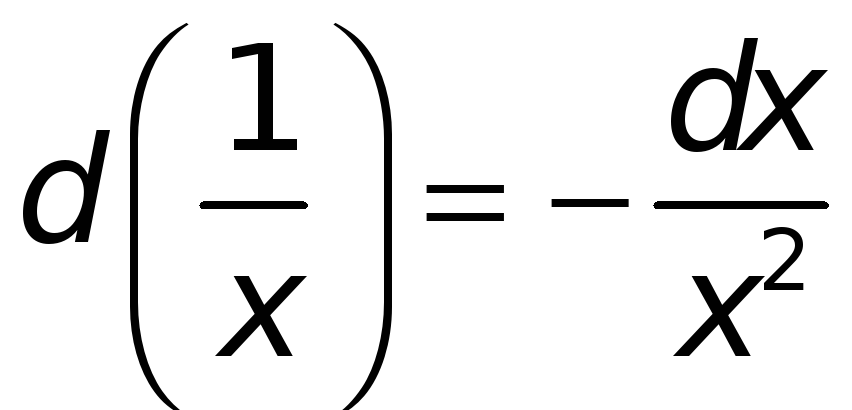 .
. -
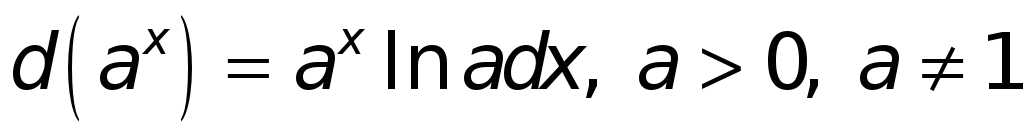 .
. -
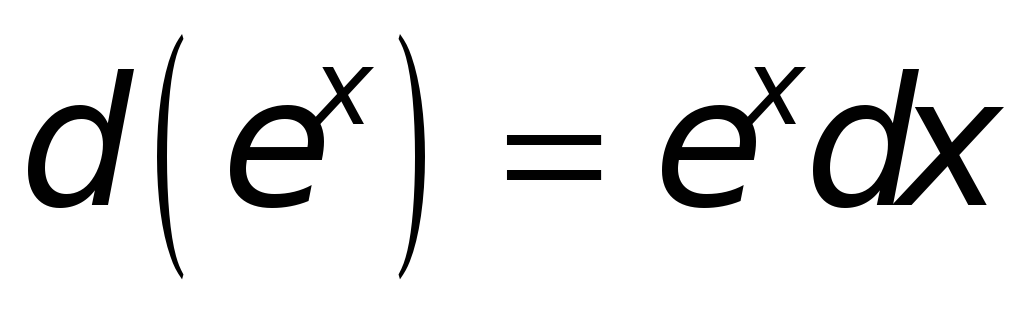 .
. -
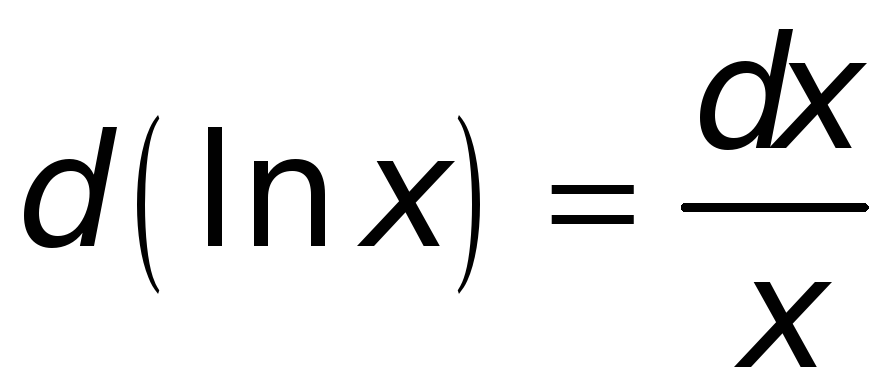 .
. -
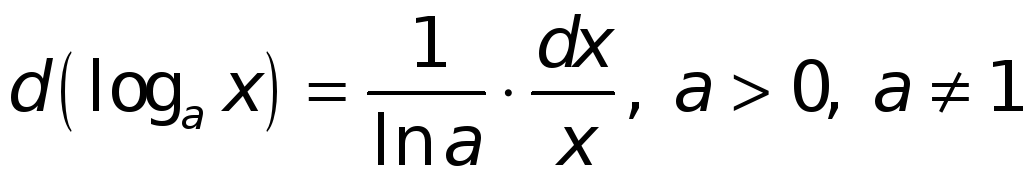 .
. -
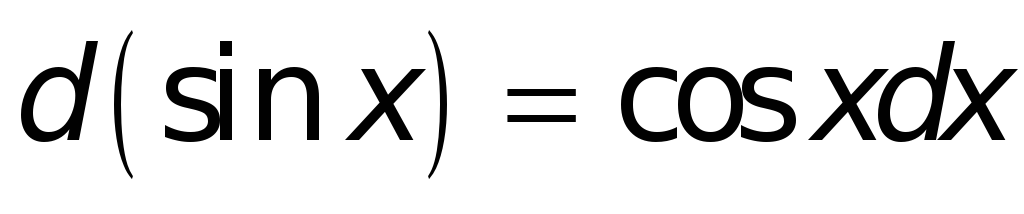 .
. -
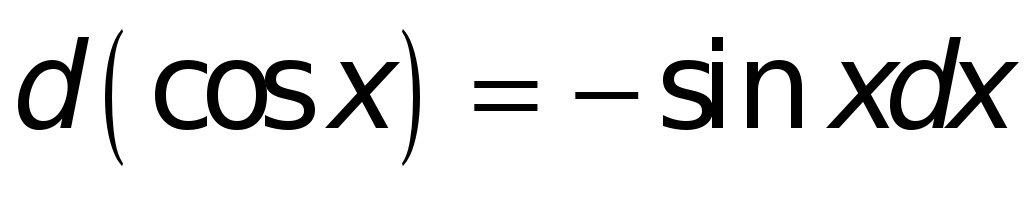 .
. -
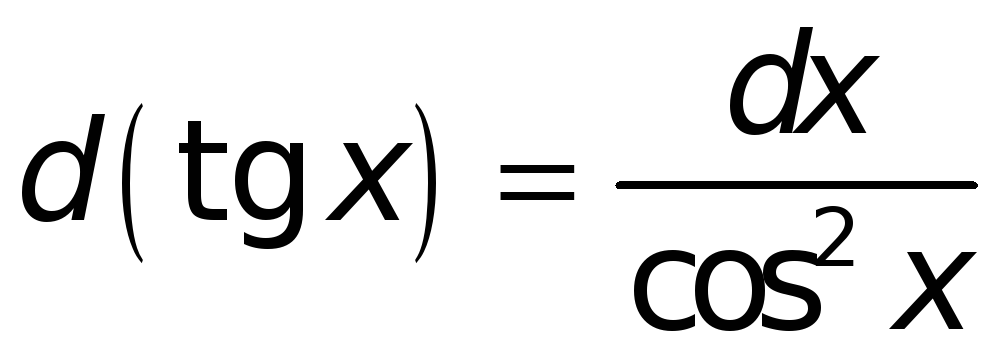 .
. -
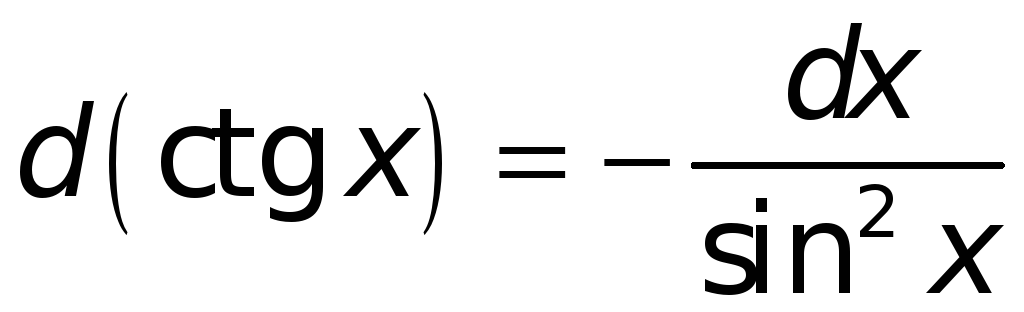 .
. -
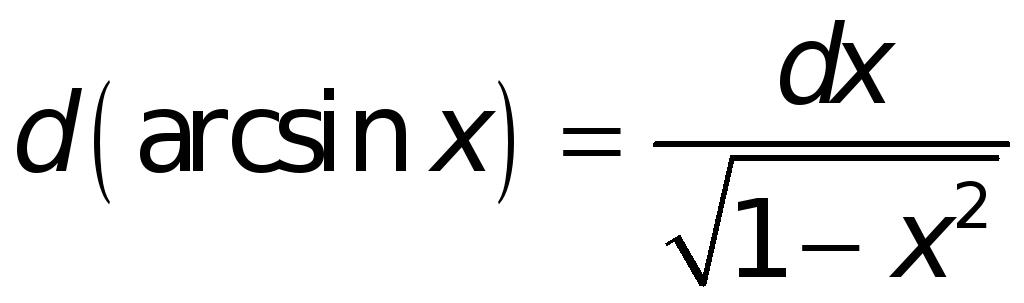 .
. -
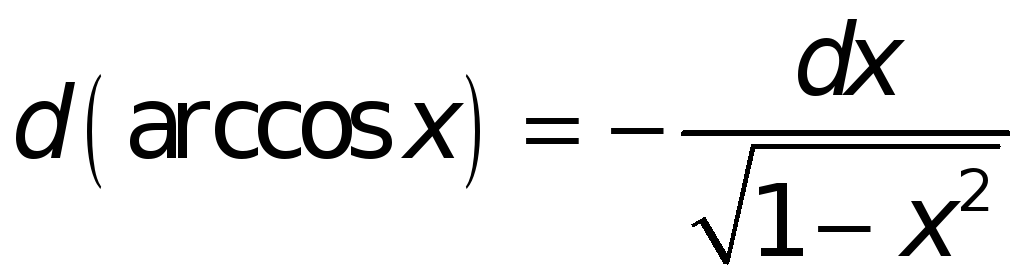 .
. -
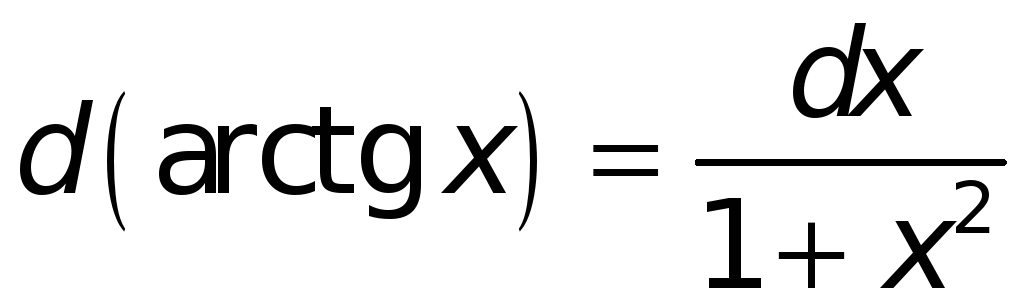 .
. -
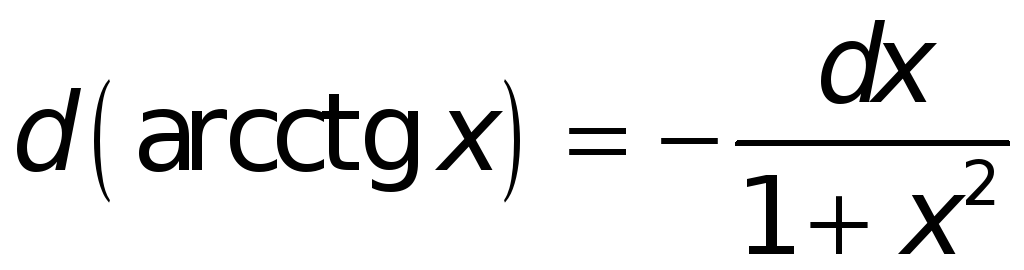 .
. -
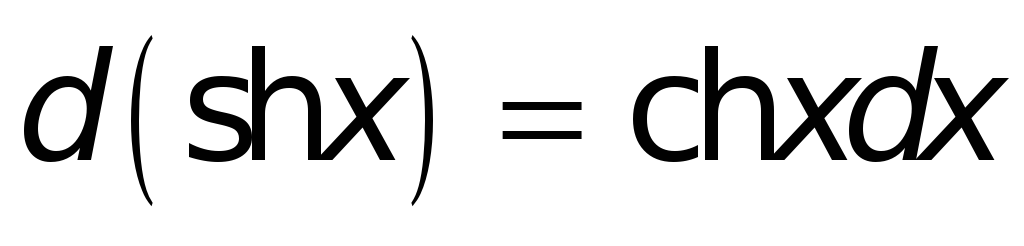 .
. -
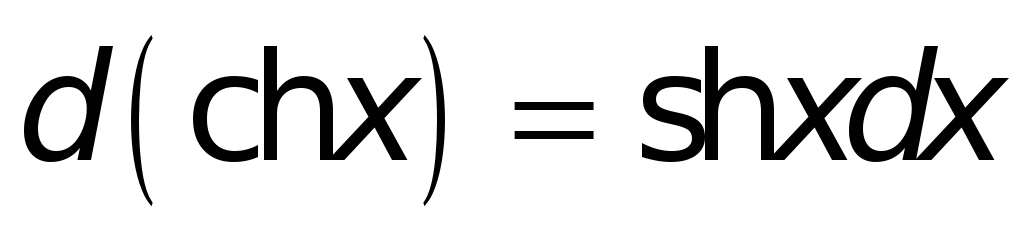 .
. -
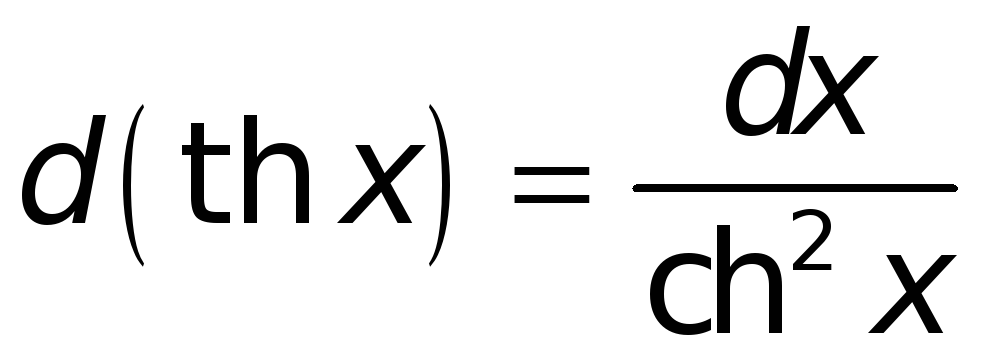 .
. -
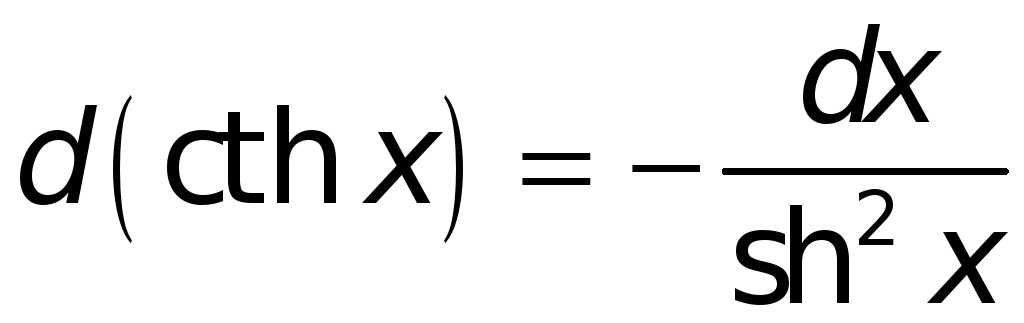 .
.
