
- •Глава 4 Производная и дифференциал § 1. Производная. Механический и геометрический смысл производной
- •4. Односторонние производные.
- •§2. Понятие дифференцируемости функции
- •§ 3. Формулы и правила вычисления производных
- •7. Простейшие правила вычисления производных.
- •12. Формула для приращения функции.
- •13. Правило дифференцирования сложной функции.
- •14. Правила дифференцирования обратных функций.
- •§ 4. Дифференциал функции
- •2. Геометрический смысл дифференциала.
- •3. Сводка формул для дифференциалов.
- •4. Дифференциал сложной функции. Инвариантность формы дифференциала.
- •§ 5. Производные высших порядков
- •2. Формула Лейбница для производной n-го порядка от произведения двух функций.
- •3. Механическое истолкование второй производной.
- •§ 6. Дифференциалы высших порядков
- •§ 7. Дифференцирование функции, заданной параметрически
- •§ 8. Основные теоремы дифференциального исчисления
- •§ 9. Формула Тейлора
- •2. Примеры разложения по формуле Тейлора.
- •§ 10. Раскрытие неопределенностей по правилу Лопиталя
- •1. Неопределенность вида .
- •2. Неопределенность вида .
- •§ 11. Признаки постоянства, возрастания и убывания функций
- •§ 12. Теория экстремальных значений функции
- •2. Исследование стационарных критических точек функции с помощью второй производной.
- •§ 13. Характер выпуклости кривой. Точки перегиба
- •§ 14. Асимптоты кривой
- •§ 15. Построение графика функции по характерным точкам
§ 3. Формулы и правила вычисления производных
1.
![]() .
.
► Выберем и закрепим
любое
![]() из промежутка
из промежутка
![]() .
Дадим этому фиксированному х
приращение
.
Дадим этому фиксированному х
приращение
![]() — любое, но такое, что
— любое, но такое, что
![]() .
Тогда
.
Тогда
![]() ,
,
и, следовательно,
![]() ,
т. е.
,
т. е.
![]() для любого
для любого
![]() из промежутка
из промежутка
![]() .
.
Таким образом,
![]() ,
т. е. производная постоянной величины
равна нулю (точка дифференцирования —
любая). ◄
,
т. е. производная постоянной величины
равна нулю (точка дифференцирования —
любая). ◄
2.
![]() .
.
► Выберем и закрепим
любое
![]() из промежутка
из промежутка
![]() .
Дадим этому фиксированному х
приращение
.
Дадим этому фиксированному х
приращение
![]() — любое, но такое, что
— любое, но такое, что
![]() .
Тогда
.
Тогда
![]() ,
,
и, следовательно,
![]() ,
т. е.
,
т. е.
![]() для любого
для любого
![]() из промежутка
из промежутка
![]() .
.
Таким образом,
![]() ,
т. е. производная независимой переменной
равна единице (точка дифференцирования
— любая). ◄
,
т. е. производная независимой переменной
равна единице (точка дифференцирования
— любая). ◄
3.
![]() ,
где
,
где
![]() — любое вещественное число.
— любое вещественное число.
Область определения
![]() степенной функции зависит от
степенной функции зависит от
![]() .
При целом
.
При целом
![]() получается рациональная функция. При
получается рациональная функция. При
![]() дробном мы имеем здесь радикал. Например,
пусть
дробном мы имеем здесь радикал. Например,
пусть
![]() — натуральное число и
— натуральное число и
![]() ;
эта функция определена для всех значений
х,
если
;
эта функция определена для всех значений
х,
если
![]() — нечетное и лишь для неотрицательных
значений х
— при
— нечетное и лишь для неотрицательных
значений х
— при
![]() четном (в этом случае мы имеем ввиду
арифметическое значение радикала).
Наконец, если
четном (в этом случае мы имеем ввиду
арифметическое значение радикала).
Наконец, если
![]() — иррациональное число, мы будем
предполагать
— иррациональное число, мы будем
предполагать
![]() (
(![]() допускается лишь при
допускается лишь при
![]() ).
).
► В области
определения функции
![]() берем любое значение
берем любое значение
![]() и закрепляем. Дадим этому фиксированному
х
приращение
и закрепляем. Дадим этому фиксированному
х
приращение
![]() — любое, но такое, что
— любое, но такое, что
![]() и точка
и точка
![]() .
Тогда
.
Тогда
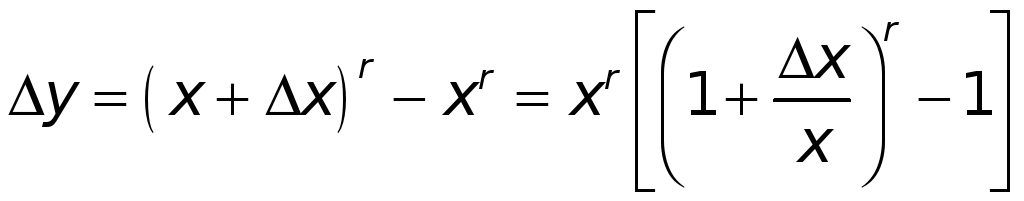 ;
;
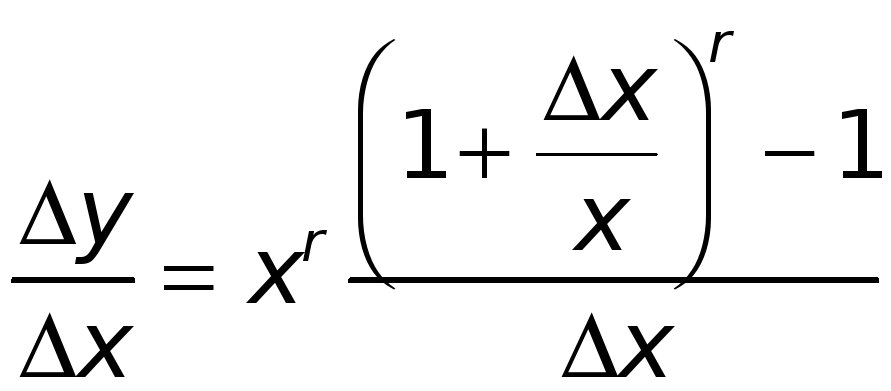 .
.
Так как
![]() — бесконечно малая величина при
— бесконечно малая величина при
![]() ,
то
,
то
 при
при
![]() .
Поэтому
.
Поэтому
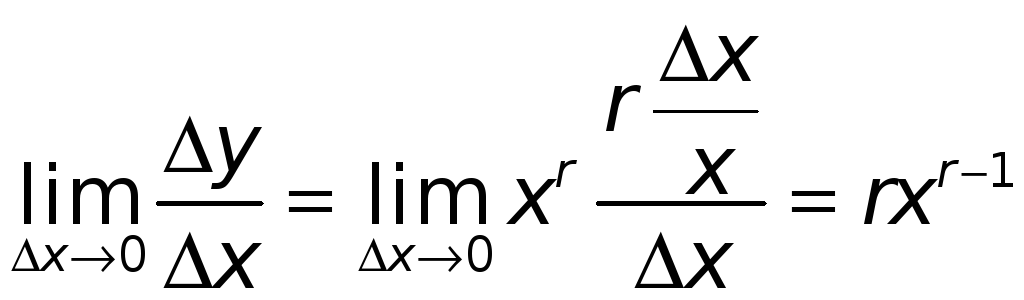 .
.
Таким образом,
![]() ,
,
![]() и
и
![]() .
◄
.
◄
Замечание.
Если точка
![]() принадлежит
принадлежит
![]() ,
то значение
,
то значение
![]() легко получить непосредственно.
легко получить непосредственно.
Частные случаи.
1)
![]() ;
;
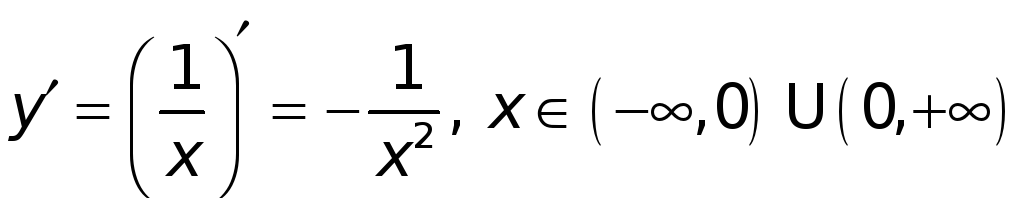 .
.
2)
![]() ;
;
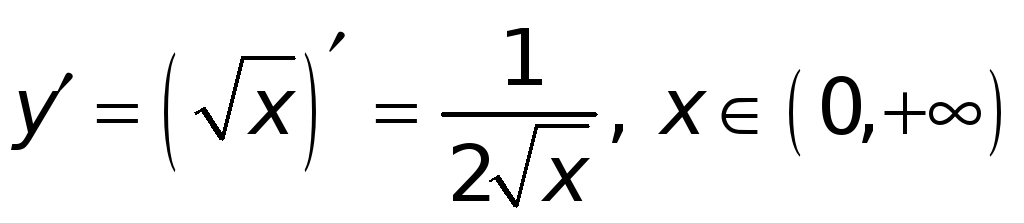 ;
;
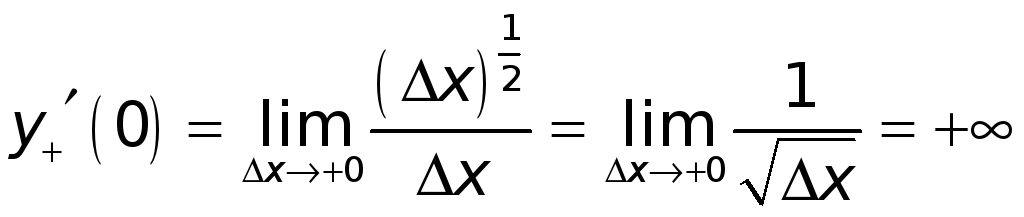
4.
![]() .
.
► Возьмем любое
х
из промежутка
![]() и закрепим. Дадим этому фиксированному
х
приращение
и закрепим. Дадим этому фиксированному
х
приращение
![]() — любое, но такое, что
— любое, но такое, что
![]() .
Тогда
.
Тогда
 ;
;
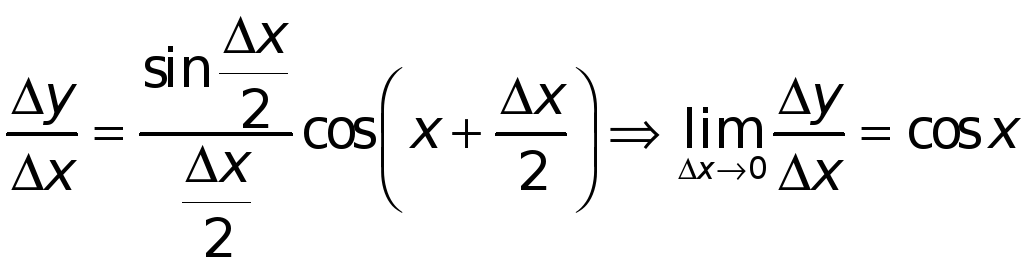 .
.
Итак,
![]() .
◄
.
◄
5.
![]() .
.
► Совершенно
аналогично предыдущему устанавливается,
что
![]() ,
,
![]() .
◄
.
◄
6.
![]() .
.
► Возьмем любое
х
из промежутка
![]() и закрепим. Дадим этому фиксированному
х
приращение
и закрепим. Дадим этому фиксированному
х
приращение
![]() — любое, но такое, что
— любое, но такое, что
![]() .
Тогда
.
Тогда
![]() .
.
Так как
![]() при
при
![]() ,
то
,
то
![]() .
Таким образом,
.
Таким образом,
![]() .
◄
.
◄
Частный случай.
![]() .
.
7. Простейшие правила вычисления производных.
I.
Пусть функции
![]() определены в некотором промежутке X
и в точке
определены в некотором промежутке X
и в точке
![]() имеют конечные производные
имеют конечные производные
![]() .
Тогда функция
.
Тогда функция
![]() в указанной точке х
также имеет конечную производную, причем
в указанной точке х
также имеет конечную производную, причем
![]() .
.
► Дадим х,
отмеченному в условиях утверждения I,
приращение
![]() — любое, но такое, что
— любое, но такое, что
![]() и точка
и точка
![]() .
Тогда функции
.
Тогда функции
![]() и
и
![]() получат соответственно приращения
получат соответственно приращения
![]() и
и
![]() ,
и их новыми значениями будут:
,
и их новыми значениями будут:
![]() и
и
![]() ;
причем
;
причем
![]() и
и
![]() .
Следовательно,
.
Следовательно,
![]()
![]() .
.
По условию,
существуют конечные
![]() ,
,
![]() ,
равные соответственно
,
равные соответственно
![]() .
А тогда
.
А тогда
![]() существует конечный, причем
существует конечный, причем
![]() .
◄
.
◄
Замечание. Полученный результат может быть легко распространен на любое конечное число слагаемых.
II.
Пусть функции
![]() определены в некотором промежутке X
и в точке
определены в некотором промежутке X
и в точке
![]() имеют конечные производные
имеют конечные производные
![]() .
Тогда функция
.
Тогда функция
![]() в указанной точке х
также имеет конечную производную, причем
в указанной точке х
также имеет конечную производную, причем
![]() .
.
► Дадим х,
отмеченному в условиях утверждения II,
приращение
![]() — любое, но такое, что
— любое, но такое, что
![]() и точка
и точка
![]() .
Тогда функции
.
Тогда функции
![]() и
и
![]() получат соответственно приращения
получат соответственно приращения
![]() и
и
![]() ,
и их новыми значениями будут
,
и их новыми значениями будут
![]() и
и
![]() .
А значит,
.
А значит,
![]()
![]()
![]() .
.
По условию существуют
конечные
![]() ,
,
![]() ,
равные соответственно
,
равные соответственно
![]() .
Кроме того,
.
Кроме того,
![]() ,
ибо функция
,
ибо функция
![]() дифференцируема в точке х,
а, следовательно, непрерывна в этой
точке (значит, бесконечно малому
приращению аргумента соответствует
бесконечно малое приращение функции).
А тогда
дифференцируема в точке х,
а, следовательно, непрерывна в этой
точке (значит, бесконечно малому
приращению аргумента соответствует
бесконечно малое приращение функции).
А тогда
![]()
![]()
Замечание.
Если
![]() ,
причем
,
причем
![]() ,
,
![]() ,
,
![]() существуют конечные, то
существуют конечные, то
![]() .
.
И вообще, если
![]() ,
причем
,
причем
![]() ,
,
![]() ,
,
![]() ,
…,
,
…,
![]() существуют конечные (и число сомножителей
— конечное число), то
существуют конечные (и число сомножителей
— конечное число), то
![]()
![]() .
.
Это соотношение устанавливается методом математической индукции.
III.
Пусть функции
![]() определены в некотором промежутке X
и в точке
определены в некотором промежутке X
и в точке
![]() имеют конечные производные
имеют конечные производные
![]() .
Пусть
.
Пусть
![]() в этой точке
в этой точке
![]() .
Тогда функция
.
Тогда функция
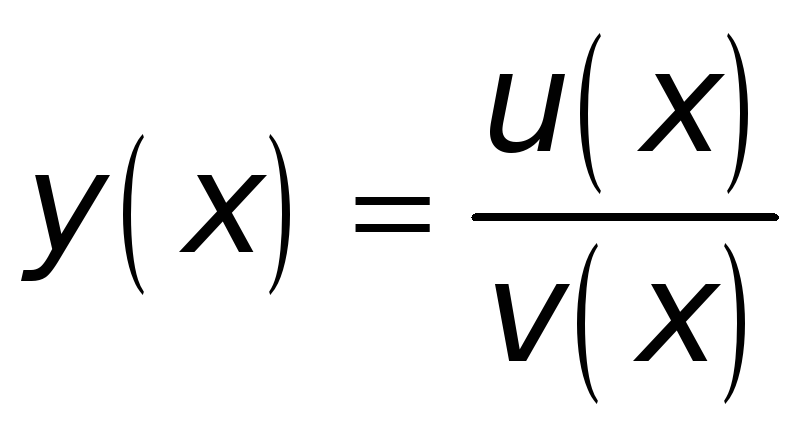 в указанной точке
в указанной точке
![]() также имеет конечную производную, причем
также имеет конечную производную, причем
 .
.
► По условию
существует конечная
![]() в точке
в точке
![]() ,
следовательно,
,
следовательно,
![]() — непрерывная в точке х0.
По условию
— непрерывная в точке х0.
По условию
![]() ,
следовательно, по теореме о стабильности
знака существует окрестность
,
следовательно, по теореме о стабильности
знака существует окрестность
![]() точки х0
такая, что
точки х0
такая, что
![]() и
и
![]() ,
,
![]() .
Дадим х0,
отмеченному в условиях утверждения
III, приращение
.
Дадим х0,
отмеченному в условиях утверждения
III, приращение
![]() — любое, но такое, что
— любое, но такое, что
![]() и точка
и точка
![]() .
Тогда функции
.
Тогда функции
![]() и
и
![]() получат соответственно приращения
получат соответственно приращения
![]() и
и
![]() ,
и их новыми значениями будут
,
и их новыми значениями будут
![]() и
и
![]() .
А значит,
.
А значит,
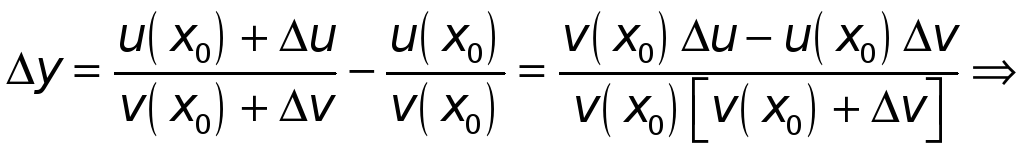
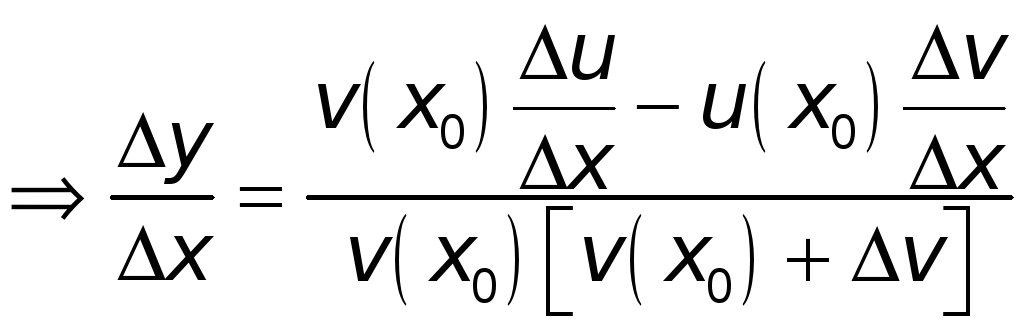 .
.
Заметим, что по условию:
![]() ;
;
![]() .
.
А тогда
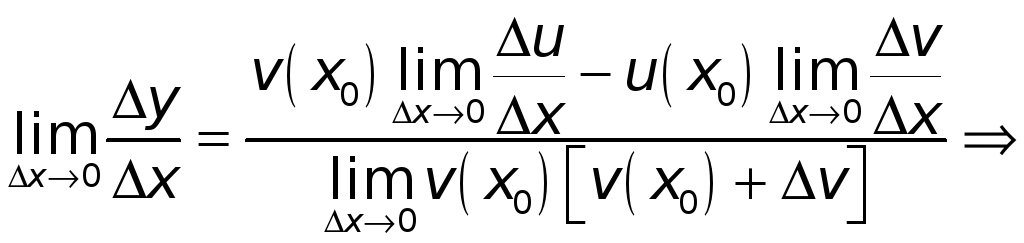
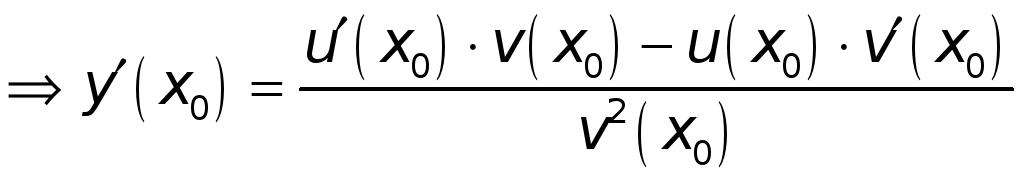 .
◄
.
◄
8.
![]() .
.
► Возьмем любое
х
из промежутка
![]() и закрепим. Дадим этому фиксированному
х
приращение
и закрепим. Дадим этому фиксированному
х
приращение
![]() — любое, но такое, что
— любое, но такое, что
![]() и точка
и точка
![]() .
Тогда
.
Тогда
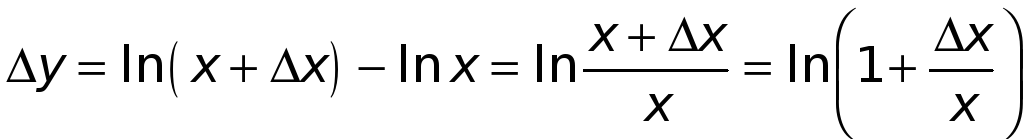 .
.
Так как
![]() — бесконечно малая величина при
— бесконечно малая величина при
![]() ,
то
,
то
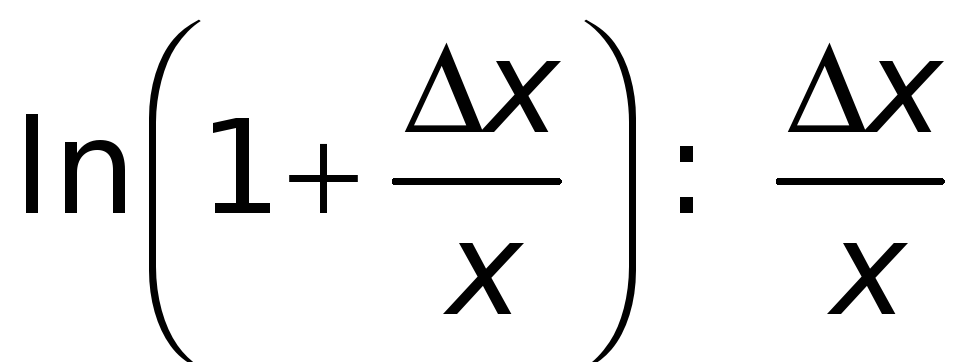 при
при
![]() .
Поэтому
.
Поэтому
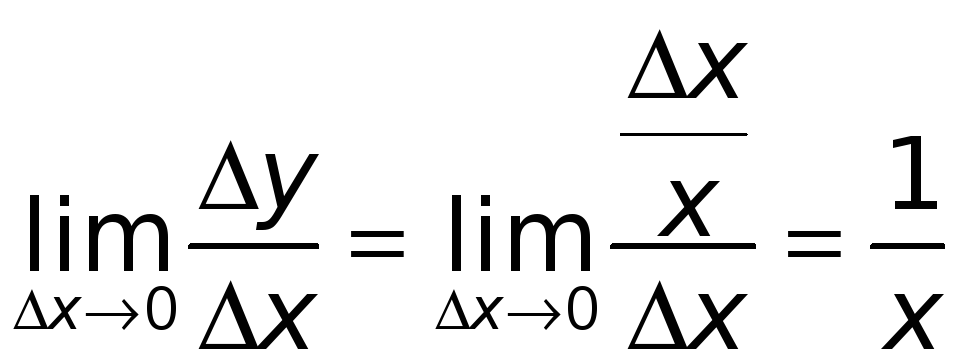 .
.
Таким образом,
![]() .
◄
.
◄
9.
![]() .
.
► Имеем
![]()
![]() ◄
◄
10.
![]() ;
;
![]() определена всюду, за исключением точек
определена всюду, за исключением точек
![]() ,
,
![]() .
.
► Имеем
![]() .
Следовательно, для
.
Следовательно, для
![]() ,
,
![]()

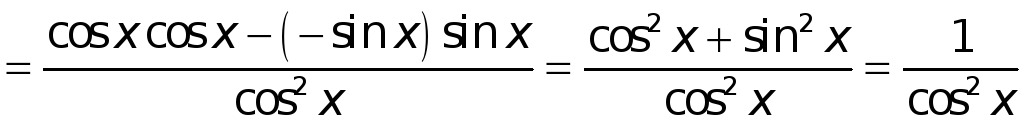 .
.
Итак,
![]() ,
если
,
если
![]() ,
,
![]() .
◄
.
◄
11.
![]() ;
;
![]() определена всюду, за исключением точек
определена всюду, за исключением точек
![]() ,
,
![]() .
.
► Совершенно
аналогично предыдущему устанавливается,
что
![]() ,
если
,
если
![]() ,
,
![]() .
◄
.
◄
