
- •010700 Физика
- •1. Цели освоения дисциплины
- •2. Место дисциплины в структуре ооп бакалавриата
- •3. Требования к результатам освоения содержания дисциплины
- •4. Структура и содержание дисциплины (модуля)
- •5. Содержание разделов (тем) дисциплины
- •Раздел 1. Понятие линейного векторного пространства.
- •Раздел 2. Общие системы линейных уравнений. Однородные системы.
- •Раздел 3. Линейная зависимость и независимость векторов. Ранг и базис векторов.
- •Раздел 4. Матрицы.
- •Раздел 5. Определители.
- •Раздел 6. Элементы векторной алгебры в аналитической геометрии.
- •Раздел 7. Координатный метод в геометрии.
- •Раздел 8. Прямая и плоскость.
- •Раздел 9. Кривые и поверхности второго порядка.
- •Раздел 10. Подпространства линейного пространства. Изоморфизм векторных пространств.
- •Раздел 11. Линейные операторы.
- •Раздел 12. Евклидово пространство (вещественное и комплексное).
- •Раздел 13. Линейные операторы, действующие в евклидовом пространстве.
- •Раздел 14. Билинейные и квадратичные формы.
- •Раздел 15. Элементы теории групп.
- •6. Образовательные технологии:
- •7. Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины и учебно-методическое обеспечение самостоятельной работы студентов
- •I семестр
- •II семестр
- •Вопросы к коллоквиумам
- •I семестр
- •II семестр
- •Примерные варианты контрольных работ
- •I семестр (3 варианта из 6)
- •II семестр (2 варианта из 10)
- •8.Учебно-методическое и информационное обеспечение дисциплины (модуля)
- •9. Материально-техническое обеспечение дисциплины (модуля)
- •2.Тематические тесты алгебре и аналитической геометрии
- •1. Матрицы и определители Тест1.
- •2. Системы линейных уравнений Тест 1
- •3. Векторная алгебра Тест 1
- •4. Прямая линия на плоскости Тест 1
- •1. Укажите, какие из следующих уравнений определяют прямую линию:
- •Прямая в пространстве Тест 1
- •Лабораторная работа
- •Ход выполнения работы
- •11. Вывод уравнения прямой по двум точкам
- •1V. Вывод уравнений прямой линии в пространстве
- •V. По результатам проведенного исследования заполните следующую таблицу. Различные уравнения прямой на плоскости и в пространстве
- •Дидактические материалы для организации самостоятельной работы студентов физического факультета по дисциплине « Линейная алгебра и аналитическая геометрия
- •1. Литература, рекомендуемая для изучения дисциплины
- •1.1. Основная литература
- •1.2. Дополнительная литература
- •2. Содержание курса линейной алгебры и аналитической геометрии
- •3. Задания для самостоятельной работы на первый семестр
- •3.1.Темы для самостоятельного изучения
- •3.2. Вопросы к коллоквиуму
- •3.3. Индивидуальная домашняя контрольная работа №1
- •3.4. Индивидуальная домашняя контрольная работа №2
- •3.5.Примерные варианты контрольной работы по аналитической геометрии Варианты № 1
- •Вариант №2
- •Вариант №3
- •4. Задания для самостоятельной работы на второй семестр
- •4.1. Темы для самостоятельного изучения
- •4.2. Вопросы к коллоквиуму
- •4.3. Индивидуальное домашнее задание № 3
- •5.4. Примерные варианты 20 - минутной самостоятельной работы по теме "Линейные преобразования"
- •5.5 Примерные варианты контрольной работы по линейной алгебре
- •6. Программа экзамена по курсу "аналитическая геометрия и линейная алгебра"
- •I семестр
- •II семестр
II семестр (2 варианта из 10)
Вариант № 1
1. Найти канонический базис и жорданову форму следующей матрицы
2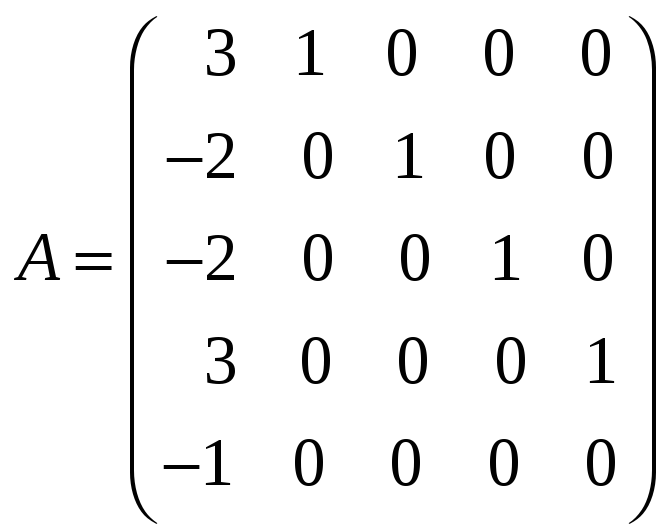 .Применяя
процесс ортогонализации, построить
ортогональный базис
подпространства,
натянутого
на
векторы
.Применяя
процесс ортогонализации, построить
ортогональный базис
подпространства,
натянутого
на
векторы
![]() .
.
3.Привести
к каноническому виду квадратичную форму
![]() .
.
Вариант №2
1. Найти канонический базис и жорданову форму следующей матрицы
2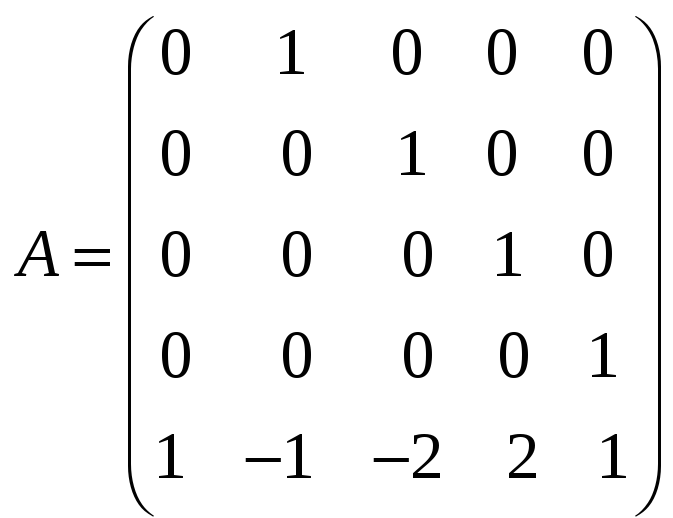 .Применяя
процесс ортогонализации, построить
ортогональный базис
подпространства,
натянутого
на
векторы
.Применяя
процесс ортогонализации, построить
ортогональный базис
подпространства,
натянутого
на
векторы
![]() .
.
3.Привести
к каноническому виду квадратичную форму
![]() .
.
8.Учебно-методическое и информационное обеспечение дисциплины (модуля)
Основная литература
-
Ильин В.А., Позняк Э.Г., Аналитическая геометрия, М., 1981
-
Ильин В.А., Позняк Э.Г., Линейная алгебра., М.,1984.
-
Головина Л.И. Линейная алгебра и некоторые ее приложения, М., 1979.
-
Клетеник Д.В. Сборник задач по аналитической геометрии., М., 1979.
-
Проскуряков И.В. Сборник задач по алгебре., М., 1970.
-
Александров П.С. Курс аналитической геометрии и линейной алгебры., М., 1979.
-
Большаков Ю.И., Медведева Л.Б., Математика для студентов в задачах и упражнениях по физике: учеб. пособие; Яросл. гос. ун-т им. П.Г. Демидова. – Ярославль: ЯрГУ, 2009.–132 с.
-
Методические указания «Дидактические материалы для организации самостоятельной работы студентов-физиков по курсу «Линейная алгебра и аналитическая геометрия».
. – Ярославль: ЯрГУ, 1997.–24 с.
Дополнительная литература
-
Мальцев А.И. Основы линейной алгебры, М., 1970
-
Гельфанд И.М. Лекции по линейной алгебре, М., 1971.
-
Федорчук В.В. Курс аналитической геометрии и линейной алгебры. Изд-во Московского ун-та, 1990.
-
Фадеев Д.К., Соминский И.С. Сборник задач по высшей алгебре, М., 1973.
9. Материально-техническое обеспечение дисциплины (модуля)
1.Методические указания «Дидактические материалы для организации самостоятельной работы студентов-физиков по курсу «Линейная алгебра и аналитическая геометрия». – Ярославль: ЯрГУ, 1997.–24 с.
Распечатка указаний приводится ниже. Это материал для студентов. Он знакомит их с программой дисциплины и всеми контрольными мероприятиями, проводимыми по ней
2.Тематические тесты алгебре и аналитической геометрии
3. Разработка лабораторной работы по теме «Уравнения прямой линии на плоскости и в пространстве»
Программа составлена в соответствии с требованиями ФГОС ВПО с учетом рекомендаций и ПрООП ВПО по направлению и профилю
Автор (ы) ______________Медведева Л.Б.______________
Рецензент (ы) _________________________
Программа одобрена на заседании __________________________________________________
(Наименование уполномоченного органа вуза (УМК, НМС, Ученый совет)
от ___________ года, протокол № ________.
2.Тематические тесты алгебре и аналитической геометрии
1. Матрицы и определители Тест1.
1. Единичная матрица – это квадратная матрица, у которой
-
все элементы равны 1;
-
все элементы первой строки равны 1;
-
все элементы, не стоящие на главной диагонали, равны 0;
-
все элементы главной диагонали равны 1, остальные равны 0;
-
все элементы либо нули, либо единицы.
2. Продолжите определение:
Треугольной матрицей называется матрица, все элементы которой, стоящие …… равны нулю.
3. Выбрать среди следующих утверждений верные утверждения:
1) любые две матрицы можно сложить;
2) любые две квадратные матрицы можно сложить;
3) любые две матрицы одинаковых размеров можно сложить;
4) любые две квадратные матрицы одного порядка можно сложить;
5) любую матрицу можно умножить на число;
6) при умножении матрицы на число 1 получится единичная матрица;
7) при умножении матрицы на число 0 получится нулевая матрица.
4. Дана матрица, имеющая размеры
![]() .
Транспонированная матрица имеет размеры
.
Транспонированная матрица имеет размеры
1)
![]() 2)
2)![]() 3)
3)![]() ,
4)
,
4)![]()
5.
Даны матрицы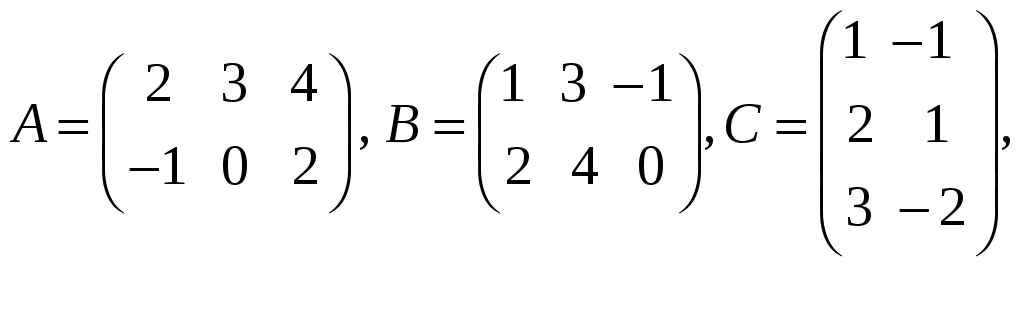
![]()
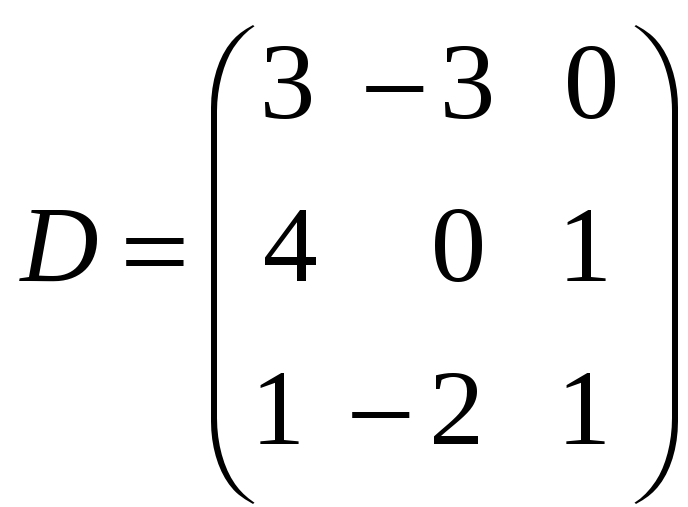 .
Какие из указанных пар можно сложить:1)
.
Какие из указанных пар можно сложить:1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)![]() ,
4)
,
4)![]() ,
5)
,
5)![]() ,
6)
,
6)
![]() .
.
-
Если матрица А имеет размеры
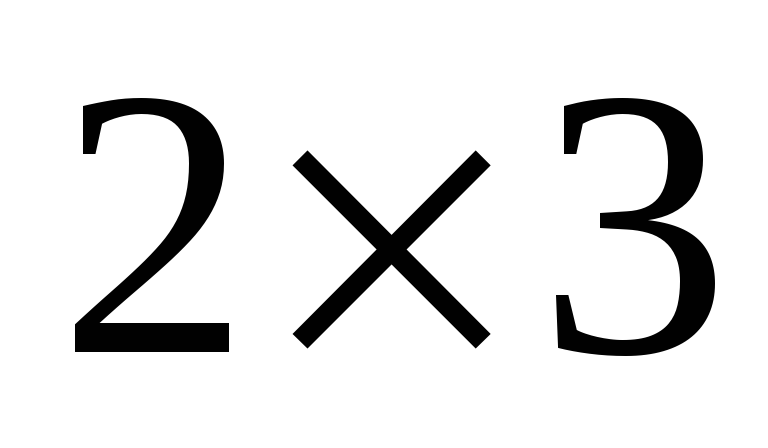 ,
матрица B
– размеры
,
матрица B
– размеры
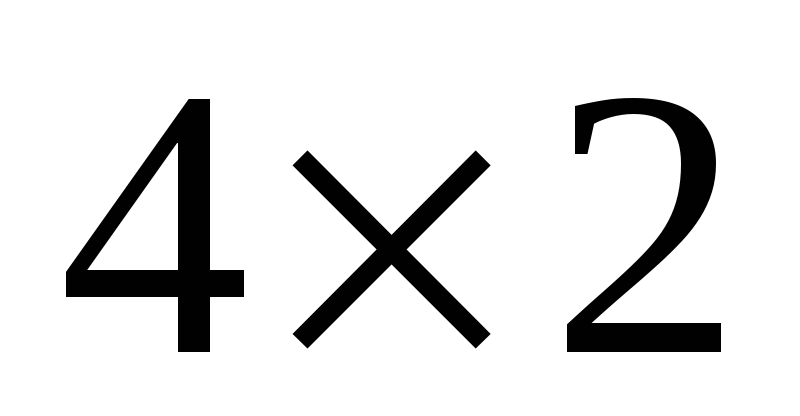 ,
матрица
,
матрица
C
– размеры
![]() ,
то матрицы АC
и BА
имеют размеры
,
то матрицы АC
и BА
имеют размеры
1)
![]() и
и
![]() ;
2)
;
2)
![]() и
и
![]() ;
3)
;
3)
![]() и
и
![]() ;
4)
;
4)
![]() и
и
![]() .
.
7.
Даны матрицы 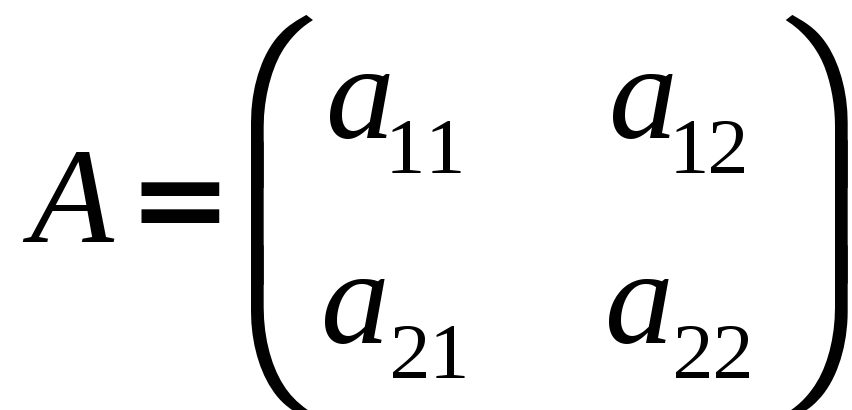 и
и
![]() .
.
Какое из указанных произведений нельзя найти:
1)
![]() 2)
2)![]() 3)
3)
![]() 4)
4)
![]() 5)
5)
![]()
8. Пусть даны матрицы
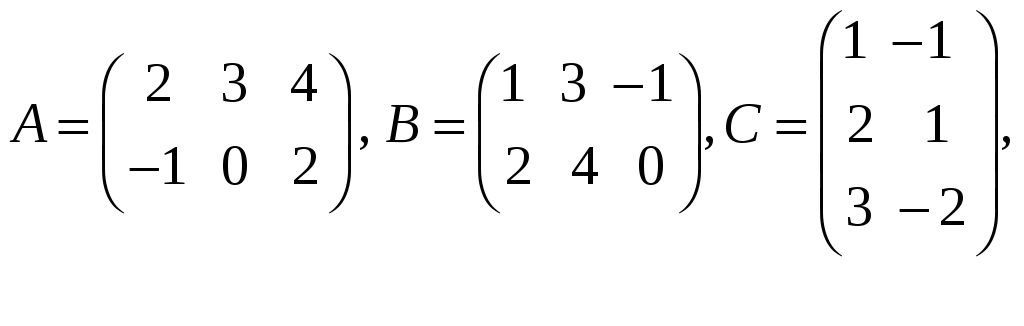
![]()
 . Укажите произведения,
которые можно найти: 1)
. Укажите произведения,
которые можно найти: 1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)![]() ,
4)
,
4)![]() ,
5)
,
5)![]() ,
6)
,
6)
![]() 7)
7)
![]() .
.
9. Если
![]() – произвольная матрица и
– произвольная матрица и
![]() – транспонированная к ней матрица, то
1)
– транспонированная к ней матрица, то
1)![]() .
.
2)![]() .
.
3)![]() .
.
4)![]() .
.
10.
Пусть
![]() и
и
![]() существует. Укажите верные утверждения:
существует. Укажите верные утверждения:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
![]() .
.
11. Ранг матрицы – это
-
число ненулевых элементов матрицы;
-
наибольший порядок ее миноров, отличных от нуля;
-
максимальное число линейно независимых строк матрицы;
-
число ненулевых миноров матрицы;
5) величина наибольшего ненулевого минора.
Тест2
1. Для матрицы B,
полученной из квадратной матрицы n-го
порядка А
перестановкой местами i-ой
строки и j-ой
строки
![]()
1)
![]() 2)
2)
![]() ;
3)
;
3)
![]() 4)
4)
![]()
2.
Если А
– квадратная матрица n-го
порядка, то для транспонированной
матрицы
![]()
1)
![]() 2)
2)
![]() ;
;
3)
![]() 4)
4)
![]()
3. Пусть А
квадратная
матрица n-го
порядка, а матрица B
получена из транспонированной матрицы
![]() перестановкой первого и последнего
столбцов. Тогда
перестановкой первого и последнего
столбцов. Тогда
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
4. Если
![]() ,
где A
– произвольная матрица второго порядка,
E
– единичная матрица, то
,
где A
– произвольная матрица второго порядка,
E
– единичная матрица, то
-
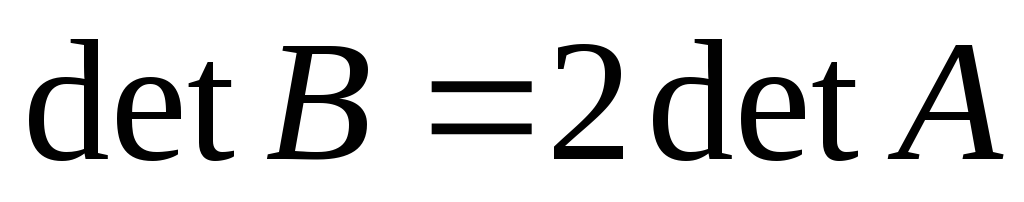 .
. -
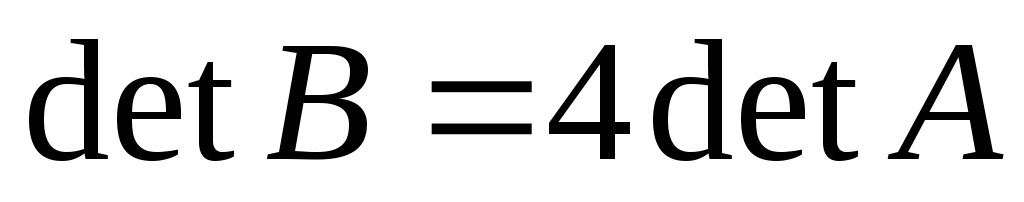 .
. -
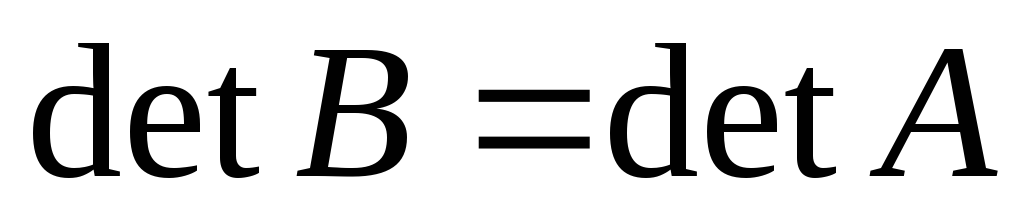 .
. -
 .
.
5. В квадратной матрице А n-го порядка i-ый столбец заменили на копию j-го столбца, оставив остальные столбцы неизменными. Определитель полученной матрицы равен
1)
![]() 2)
2)
![]() 3)
0 4)
3)
0 4)
![]()
6. В квадратной матрице А строку умножим на число k (–1<k<0). Для полученной матрицы B:
1)
![]() 2)
2)
![]() ;
3)
;
3)
![]() 4)
4)
![]()
7. В квадратной
матрице А
i-ую
строку заменили на сумму i-ой
и j-ой
строк (![]() .
Для полученной матрицы B
.
Для полученной матрицы B
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() 4)
4)
![]() .
.
8. В квадратной матрице А n-го порядка изменили знак каждого элемента i-ой строки на противоположный. Определитель полученной матрицы равен
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
9. В квадратной
матрице А
все элементы первой и последней строки
умножили на число k
![]() .
Определитель полученной матрицы равен
.
Определитель полученной матрицы равен
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
.
10. Для квадратной матрицы А сумма произведения элементов i-ой строки на их алгебраические дополнения равна
1) 0; 2)
![]() 3)
3)
![]() 4)
4)
![]()
11. Если
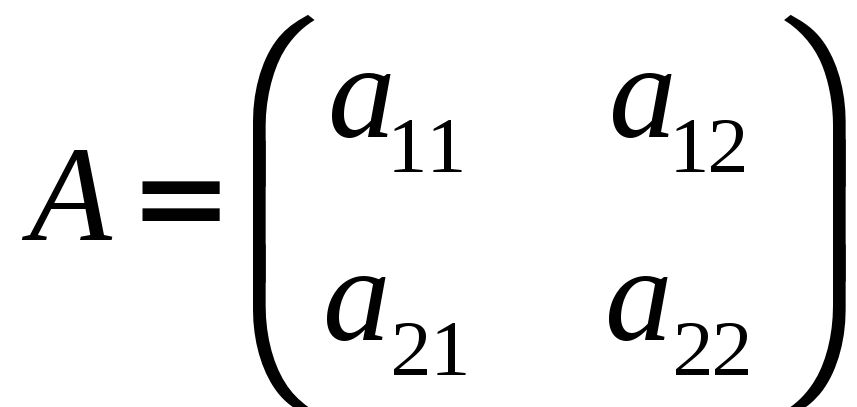 – произвольная матрица, а
– произвольная матрица, а
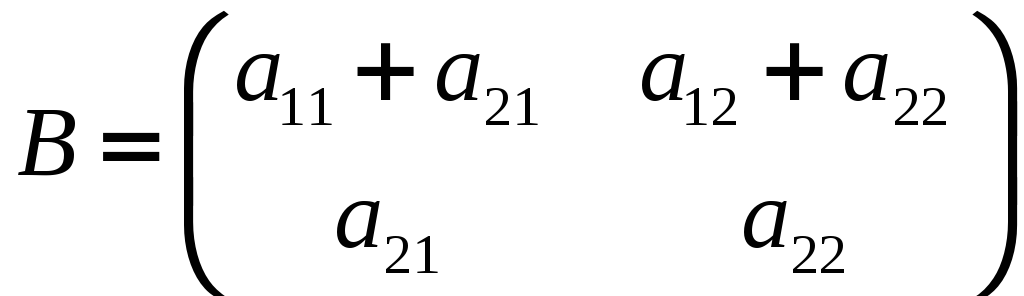 ,
то
,
то
-
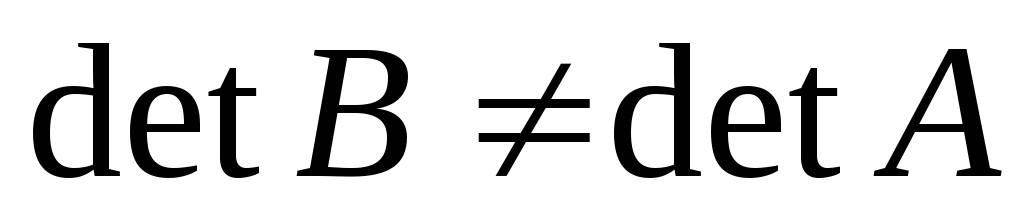 ;
2)
;
2)
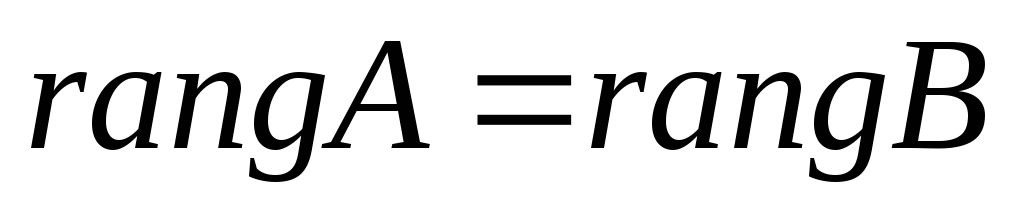 ;
3)
;
3)
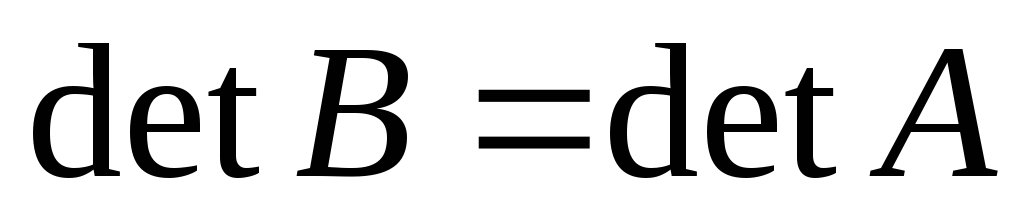 +1;
4)
+1;
4)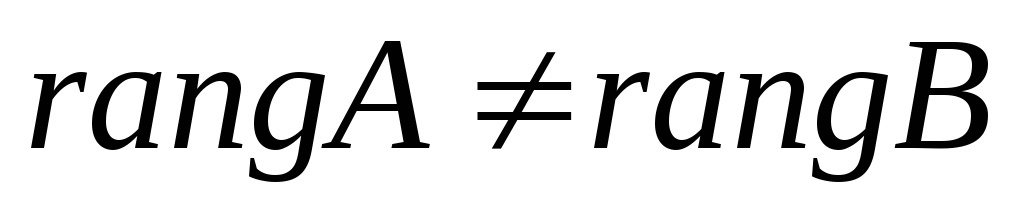 ;
;
5)
![]() .
.
12. Определитель квадратной матрицы равен 0, если
-
элементы одной из строк пропорциональны элементам какого-нибудь столбца;
-
сумма всех элементов матрицы равна 0;
-
элементы, по крайней мере, двух строк пропорциональны;
-
произведение диагональных элементов равно 0.
-
Алгебраическое дополнение элемента
 матрицы
матрицы
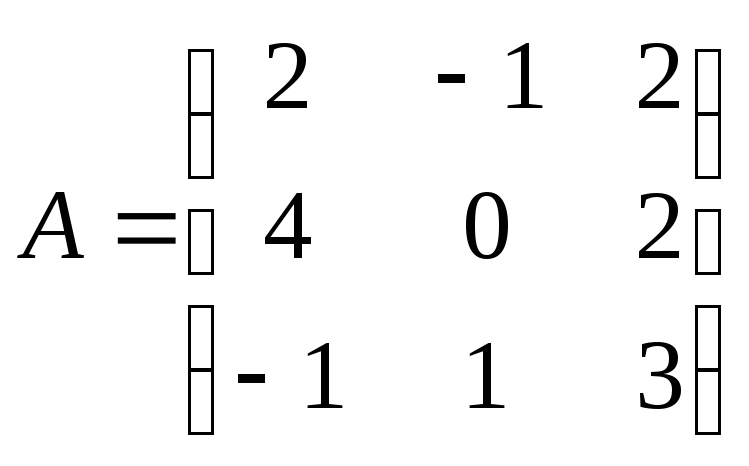 имеет вид:
имеет вид:
a)![]() ;
b)
;
b)
![]() ; c)
; c)
![]() ;
d)
;
d)
![]() ;
;
14. Сумма произведений элементов какой-нибудь строки в определителе на алгебраические дополнения соответствующих элементов другой строки равна:
-
1.
-
0.
-
этому определителю.
-
другому определителю, отличному от 0.
15. Если А – треугольная матрица порядка n, то ее определитель равен
-
0.
-
1.
-
произведению диагональных элементов.
-
максимальному диагональному элементу.
