Ход выполнения работы

1.Вывод уравнения прямой, заданной точкой и направляющим вектором

1. Сделайте рисунок, соответствующий рассматриваемому заданию прямой, обозначьте заданную точку символом А, а направляющий вектор символом .

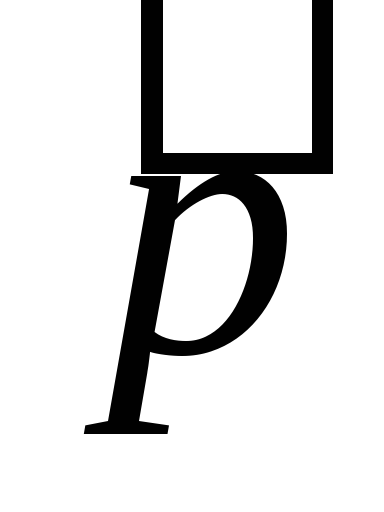2. Выделите характеристическое свойство точек прямой, проходящей через точку А и имеющей направляющим вектор .

3. Запишите это условие в виде векторного уравнения.

4. Выразите из полученного уравнения радиус-вектор текущей (произвольной) точки этой прямой.

Полученное уравнение называется векторным параметрическим

уравнением прямой по точке и направляющему вектору, занумеруйте его числом (1).

Роль числа – параметра, входящего в уравнение прямой, состоит в том , что оно определяет положение точки на прямой: каждому значению этого параметра соответствует единственная точка на прямой и наоборот, каждой точке прямой соответствует вполне определенное число.

5. Запишите уравнение (1) в координатной форме. Для этого задайте точку А , текущую точку прямой и направляющий вектор координатами в некоторой (выбранной Вами ) системе координат.

Полученные уравнения называются параметрическими уравнениями прямой на плоскости по точке и направляющему вектору в координатной форме. Занумеруйте их числом (2).

6. Исключите из параметрических уравнений (2) параметр. Получите уравнение, которое называется каноническим уравнением прямой на плоскости. Поставьте ему в соответствие номер (3).

7. Приведите уравнение (3) к виду x + By + C = 0, используя свойство пропорции и переобозначение коэффициентов. Убедитесь, что в уравнении

x + By + C = 0 (4)

коэффициенты  и B не равны 0 одновременно.

Докажите, что всякое линейное уравнение (4), в котором коэффициенты  и B не равны 0 одновременно, является уравнением прямой линии в некоторой системе координат ( см. 2, с.45 или 1, с. 110).

8. подумайте с сформулируйте геометрический смысл коэффициентов при переменных в уравнении (4).

Уравнение (4) называется общим уравнением прямой на плоскости.

9. Выразите из уравнения (4) переменную y и получите уравнение вида

y = kx + b (5)

Такое уравнение называется уравнением прямой с угловым коэффициентом

10. Приведите уравнение (4) к виду

(6)

При каких условиях оно может быть приведено к этому виду? Выясните, каков геометрический смысл параметров этого уравнения, найдя пересечение прямой (6) с осями координат.

Уравнение (6) называется уравнением прямой в отрезках. Объясните почему.

11. Вывод уравнения прямой по двум точкам

1. Сделайте рисунок, иллюстрирующий задание прямой двумя точками.

2. Сведите этот способ задания к предыдущему, найдя направляющий вектор заданной прямой.

3. Запишите уравнения вида (1), (2) и (3) в этом случае.

Они будут соответственно называться:

а) векторным параметрическим уравнением прямой по двум точкам на плоскости (7),

б) параметрическими уравнениями прямой на плоскости по двум точкам в координатной форме (8),

в) каноническим уравнением прямой на плоскости по двум

точкам (9).

111. Вывод уравнения прямой на плоскости по точке и нормальному вектору.

1. Сделайте рисунок, иллюстрирующий задание прямой в этом случае, обозначив заданную точку символом А, а нормальный вектор символом .

2. Выделите характеристическое свойство точек прямой, проходящей через точку А перпендикулярно вектору .

3. Запишите это условие в виде векторного уравнения .

4. Выбрав прямоугольную декартову систему координат и задав в ней координаты точки А, текущей точки прямой и нормального вектора к этой прямой, запишите полученное в пункте 3 уравнение в координатной форме. Получите уравнение

, (10)

которое называется уравнениями прямой на плоскости по точке и нормальному вектору.