4. Рекомендуемая литература.

4.1. Артоболевский И.И. Теория механизмов и машин: Учеб. Для втузов.-4-е изд., перераб. И доп.-М.: Наука. Гл. ред. Физ.-мат. Лит., 1988.-640 с.

4.2. Прикладная механика: Сборник задач /В.П. Бардзиловский.-К.: Вища шк. Головное изд-во, 1986.-190 с.

ЛАБОРАТОРНАЯ РАБОТА №7

Тема работы: Кинематический анализ плоского рычажного механизма.

Цель работы:

- изучить методики кинематического анализа плоских рычажных механизмов;

- освоить основы программирования задач кинематического анализа механизмов.

1. Необходимые теоретические сведения

Кинематический анализ механизмов производится с целью определения законов движения выходных и передаточных звеньев по заданным законам движения входных звеньев. Результаты анализа позволяют проектировщику судить о возможности (или о невозможности) при помощи данного механизма осуществить рабочий процесс, изменить некоторые параметры его звеньев для получения требуемых законов движения выходных звеньев или вообще принять решение об изменении структуры механизма, получить исходные данные для последующего динамического анализа механизма.

Основные задачи кинематического анализа:

1. Определение положений звеньев в пространстве и траекторий движения их характерных точек;

2. Определение линейных скоростей и ускорений характерных точек и угловых скоростей и ускорений звеньев.

Для проведения кинематического анализа механизма должна быть задана его кинематическая схема, а также законы движения входных звеньев как некоторые функции времени.

1.1. Открытые кинематические цепи

Рассмотрим плоский механизм с открытой (разомкнутой) кинематической цепью, представленный на рисунке 1.

Рисунок1 - Плоская пятизвенная открытая кинематическая цепь

Степень подвижности данной цепи равна 4, следовательно, положение ее звеньев на плоскости определяется четырьмя независимыми обобщенными координатами⁸. В качестве таких координат выберем три относительных угла поворота и линейное перемещение звена 4 относительно звена 3. Предположим, что точка , принадлежащая звену 4, одновременно принадлежит и другим звеньям цепи. Ее декартовы координаты в системах координат, жестко связанных с каждым из звеньев, представлены в виде системы линейных алгебраических уравнений (1):

(1)

Решение данной системы относительно неизвестных , являющихся функциями четырех независимых обобщенных координат , находится любым из известных аналитических или численных методов.

В задачах большой размерности (например, при числе неизвестных больше четырех) целесообразно использование различных прикладных математических программ. Ниже приводится пример программы для нахождения решения системы (1) в системе аналитических вычислений Maple V [2,3].

> restart;

> eq1:=-xd3+xd4+l3:

> eq2:=-yd3+yd4+y43:

> eq3:=-xd2+xd3*cos(f32)-yd3*sin(f32)+l2:

> eq4:=-yd2+xd3*sin(f32)+yd3*cos(f32):

> eq5:=-xd1+xd2*cos(f21)-yd2*sin(f21)+l1:

> eq6:=-yd1+xd2*sin(f21)+yd2*cos(f21):

> eq7:=-xd0+xd1*cos(f10)-yd1*sin(f10):

> eq8:=-yd0+xd1*sin(f10)+yd1*cos(f10):

> res:=solve({eq1,eq2,eq3,eq4,eq5,eq6,eq7,eq8}, {xd3,yd3,xd2,yd2,xd1,yd1,xd0,yd0}):

> assign(res);

Система (1) и ее решение могут быть представлены и в матричной форме, что для задач большой размерности позволяет получать более компактные записи при промежуточных преобразованиях. Для кинематического анализа механизма, рассмотренного выше, такое решение представлено следующим фрагментом программы:

> restart;

> with(linalg):

> A:=matrix (8,8,[1, 0, 0, 0, 0, 0, 0, 0,

0, 1, 0, 0, 0, 0, 0, 0,

-cos(f32), sin(f32), 1, 0, 0, 0, 0, 0,

-sin(f32), -cos(f32), 0, 1, 0, 0, 0, 0,

0, 0, -cos(f21), sin(f21), 1, 0, 0, 0,

0, 0, -sin(f21), -cos(f21), 0, 1, 0, 0,

0, 0, 0, 0, -cos(f10), sin(f10), 1, 0,

0, 0, 0, 0, -sin(f10), -cos(f10), 0, 1]);

> B:=inverse(A):

> C:=matrix (8,1,[xd4+l3, yd4+y43, l2, 0, l1, 0, 0, 0]);

> res:=multiply (B,C):

Как видно, элементы матриц (квадратной матрицы коэффициентов при неизвестных) и (матрицы-столбца свободных членов) взяты из уравнений системы (1), а элементы матрицы - являются решениями этой системы и однозначно определяют положения всех звеньев механизма в зависимости от значений независимых обобщенных координат.

Рассмотрим теперь общий матричный метод решения задач кинематики плоских механизмов с открытыми кинематическими цепями, звенья которых образуют вращательные или поступательные кинематические пары⁹.

Выделим два звена произвольной кинематической цепи, образующих вращательную кинематическую пару (рисунок 2). С каждым из звеньев жестко связывается плоская декартова ортогональная система координат, ориентированная так, что ось абсцисс совпадает с направлением звена. Тогда, при повороте одного из звеньев этой пары относительно другого (условно неподвижного) на некоторый угол , поворачивается и связанная с ним система координат.

Пусть координаты точки в системе 2:, тогда, в системе 1 они будут равны, соответственно:

(2)¹⁰

Рисунок 2 - Системы координат, связанные со звеньями, образующими вращательную кинематическую пару пятого класса

В матричной форме система (2) примет следующий вид:

, (3)

где - матрица вращения, - матрица-столбец, характеризующая смещение начала системы 2 относительно начала системы 1 вдоль оси .

Матричное уравнение (3) может быть представлено и в другом виде, если его дополнить тождественным равенством :

, (4)

где - однородная матрица преобразования координат на плоскости, одновременно учитывающая поворот и смещение систем координат относительно оси ¹¹.

В случае, когда звенья, образующие кинематическую пару движутся друг относительно друга поступательно, имеет место параллельный перенос системы координат (см. рис.3). Тогда:

или: . (5)

В матричном уравнении (5) однородная матрица преобразования координат на плоскости является частным случаем матрицы , для которой .

Рисунок 3 - Системы координат, связанные со звеньями, образующими поступательную кинематическую пару пятого класса

Использование однородных матриц преобразования координат позволяет в некоторой степени формализовать вывод уравнений связей, ограничивающих относительные движения звеньев кинематических цепей, а также получить достаточно просто (без вычисления обратной матрицы) их решения относительно искомых параметров и, таким образом, решить задачу о положениях звеньев кинематической цепи и траекториях их характерных точек. Так, для механизма, представленного на рис.1 получим:

,

,

,

.

После последовательной подстановки правых частей приведенных выше равенств будем иметь:

, (6)

restart; with(linalg):

> t43:=matrix([[1, 0, y43], [0, 1, l3], [0, 0, 1]]):

> t32:=matrix([[cos(f32),-sin(f32),l2],[sin(f32),cos(f32),0],[0,0,1]]):

> t21:=matrix([[cos(f21),-sin(f21),l1], [sin(f21),cos(f21),0], [0,0,1]]):

> t10:=matrix([[cos(f10),-sin(f10),0], [sin(f10),cos(f10),0], [0,0,1]]):

> t:=combine(simplify(multiply(t10,t21,t32,t43)),trig):

> sv:=matrix(3,1,[xa4,ya4,1]): res:=simplify(multiply(t,sv)):

Результаты расчета

> xa0:=combine(simplify(res[1,1]),trig);

xa0 := xa4 cos(f21 + f32 + f10) - ya4 sin(f21 + f32 + f10) + cos(f10) l1 +

y43 cos(f21 + f32 + f10) - l3 sin(f21 + f32 + f10) + l2 cos(f10 + f21)

> ya0:=combine(simplify(res[2,1]),trig);

ya0 := xa4 sin(f21 + f32 + f10) + y43 sin(f21 + f32 + f10) + sin(f10) l1 +

l3 cos(f21 + f32 + f10) + ya4 cos(f21 + f32 + f10) + l2 sin(f10 + f21).

1.2. Замкнутые кинематические цепи

Для механизмов, представляемых замкнутыми (закрытыми) кинематическими цепями, системы уравнений связей, определяющие положения звеньев и траектории их характерных точек на плоскости (в пространстве), как правило, нелинейны относительно обобщенных координат, поэтому методы их кинематического анализа имеют некоторые особенности по сравнению с изложенными выше.

Метод размыкания кинематической цепи

Каждая замкнутая кинематическая цепь может быть представлена в виде нескольких открытых кинематических цепей, если условно разомкнуть одну или несколько кинематических пар. Тогда, для каждой из таких открытых цепей, применим описанный выше общий метод кинематического анализа, с помощью которого определяются положения элементов каждой из разомкнутых кинематических пар в абсолютной системе координат. Приравнивая координаты соответствующих элементов кинематических пар (для каждой из двух открытых кинематических цепей, полученных размыканием одной и той же кинематической пары), получают систему нелинейных уравнений связей, решение которой позволяет определить все обобщенные координаты исходной кинематической цепи как функции независимых обобщенных координат.

Рассмотрим четырехзвенный кулисный механизм, представленный на рисунке 4.

Рисунок 4 - Размыкание кинематической пары А кулисного механизма

Для открытой кинематической цепи: стойка (0) – кривошип (1), однородные координаты центра элемента кинематической пары , принадлежащего звену 1 в системе координат - ; однородная матрица преобразования системы координат относительно - ; тогда, однородные координаты центра этого элемента кинематической пары в системе координат 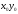равны

, (7)

где - длина звена 1, - угол поворота системы координат относительно 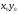. Аналогично, для открытой кинематической цепи: стойка (0) – кулиса (3) – камень (2):

,

тогда:

, (8)

где - расстояние по оси ординат межу кинематическими парами и 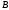; - переменная величина, равная расстоянию между кинематическими парами и (одна из обобщенных координат); - угол поворота системы координат относительно .

Приравнивая правые части равенств (7) и (8), получим систему уравнений связей рассматриваемой кинематической цепи:

. (9)

Ниже приводится один из вариантов решения системы (9) при м и м относительно обобщенных координат и с представлением результатов в графической форме.

> restart;

> eq1:=l1*cos(f1)-l3*cos(f3):

> eq2:=l1*sin(f1)-l3*sqrt(1-cos(f3)^2)+a:

> res:=solve({eq1,eq2},{l3,f3}): assign(res): l1:=0.2:a:=0.4:

> plot(-l3,f1=0..4*Pi);

> plot(180-(f3*180/Pi),f1=0..4*Pi);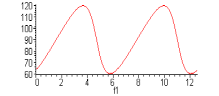

Конец расчета.

Метод замкнутых векторных контуров.

Каждая замкнутая кинематическая цепь может быть представлена в виде расчетной модели, представляющей собой один или несколько замкнутых многоугольников (контуров), построенных на векторах, совпадающих по длине и направлению с отрезками, соединяющими точки, связанные с элементами различных кинематических пар. При таком представлении следует иметь в виду, что не все возможные замкнутые контуры, которые можно составить для конкретной кинематической цепи (механизма) будут независимыми. Это означает, что некоторые из них могут быть образованы путем различных комбинаций с векторами других контуров. Следовательно, число замкнутых векторных контуров расчетной модели кинематической цепи должно быть таким, чтобы координаты векторов, входящих в них, однозначно определялись как функции независимых обобщенных координат цепи.

В качестве примера рассмотрим механизм, представленный на рисунке 5. Для данного механизма возможны несколько замкнутых контуров, например: и т.д. Первые три контура являются зависимыми, т.к. каждый из них может быть представлен в виде комбинации векторов двух других, а последний - предполагает введение дополнительной обобщенной координаты и, поэтому, является нерациональным. Таким образом, представим модель механизма в виде двух независимых контуров: и , что позволяет записать систему двух векторных уравнений:

. (10)

С целью формализовать вывод уравнений связей механизма, векторы системы (10) будем представлять в виде комплексных чисел, которые можно рассматривать как аналоги векторов при графическом изображении на плоскости, тогда:

. (11)

Рисунок 5 - Механизм сбалансированного манипулятора и его векторная модель

С учетом выражений (11) система (10) примет следующий вид:

. (12)

Приравняв коэффициенты при действительных и мнимых частях комплексных уравнений системы (12), получим систему четырех нелинейных уравнений связей механизма с четырьмя неизвестными обобщенными координатами (переменная - независимая обобщенная координата):

. (13)

Процесс вывода системы уравнений связей механизма (13) и ее аналитическое решение достаточно эффективно реализуются в системе Maple V, что иллюстрируется следующей программой:

> restart;

Подпрограмма: действительная часть комплексного числа

> Rez:=proc(z,i): subs(i=0,z); RETURN(%) end:

Подпрограмма: мнимая часть комплексного числа

> Imz:=proc(z,i): subs(i=1,z)-Rez(z,i); RETURN(%) end:

Комплексные уравнения замкнутых контуров

> eq1:=z0-z4+z3: eq2:=z4n-z5-z0-z2:

Комплексные числа, образующие замкнутые контуры

> z0:=s+i*r: z2:=l2*(cos(f2)+i*sin(f2)): z3:=l3*(cos(f3)+i*sin(f3)):

> z4:=l4*(cos(f4)+i*sin(f4)): z4n:=l4n*(cos(f4)+i*sin(f4)):

> z5:=l5*(cos(f5)+i*sin(f5)):

Система нелинейных уравнений связей механизма

> eq01:=Rez(eq1,i); eq02:=simplify(Imz(eq1,i));

> eq03:=Rez(eq2,i); eq04:=simplify(Imz(eq2,i));

Распечатка выведенной системы уравнений связей

eq01 := s - l4 cos(f4) + l3 cos(f3)

eq02 := r - l4 sin(f4) + l3 sin(f3)

eq03 := l4n cos(f4) - l5 cos(f5) - s - l2 cos(f2)

eq04 := l4n sin(f4) - l5 sin(f5) - r - l2 sin(f2)

Размеры звеньев механизма

r:=4: l2:=6: l3:=8: l4:=6: l4n:=12: l5:=8:

Решение системы нелинейных уравнений связей

> res:= solve({eq01,eq02,eq03,eq04},{f2,f3,f4,f5}): assign(res);

Графическое представление обобщенных координат и как функций независимой обобщенной координаты

> plot(f4*180/Pi, s=12..5); plot(f3*180/Pi, s=12..5);

f2=f2(s) f3=f3(s)

Выведенные зависимости могут быть использованы для определения траекторий движения характерных точек звеньев механизма, например:

декартовы координаты точки :

> xc:=l4n*cos(f4)+l5*cos(Pi+f5):

> yc:=l4n*sin(f4)+l5*sin(Pi+f5):

Траектория движения точки :

> plot ( [xc, yc, s=12..5] );

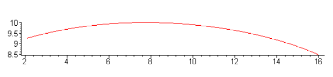
При более детальном анализе в программах следует предусматривать отделение решений системы уравнений связей типа (13), соответствующих рассматриваемому варианту сборки механизма, определение области изменения независимой обобщенной координаты при заданных размерах звеньев, выяснение возможности механизма в некоторых положениях приобретать избыточную подвижность и т.д.

1.3. Кинематические передаточные функции механизмов.

Функцией положения механизма (кинематической передаточной функцией нулевого порядка) называется функциональная зависимость обобщенной координаты выходного звена от независимых обобщенных координат входных звеньев, заданная в явном или неявном виде: или ,

где 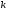- число независимых обобщенных координат (степень подвижности механизма); - номер одного из выходных звеньев механизма.

Функция положения механизма является его собственной (геометрической) характеристикой, не зависящей явно от времени, позволяющая при заданных значениях каждой из независимых обобщенных координат из областей их возможного изменения, однозначно определить обобщенную координату выходного звена.

Для механизмов со степенью подвижности, равной 1, функция положения приобретает следующий вид:

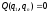или . (14)

Кинематической передаточной функцией первого порядка для механизма со степенью подвижности, равной 1, называется первая производная функции положения по независимой обобщенной координате. Кинематической передаточной функцией второго порядка для механизма со степенью подвижности, равной 1, называется вторая производная функции положения по независимой обобщенной координате¹². Как и функция положения, кинематические передаточные функции первого и второго порядков явно не зависят от времени.

Как было показано выше, функция положения механизма зависит от связей, ограничивающих движения его звеньев и может быть определена из решения системы уравнений связей. Предположим, что такая функция определена и имеет вид: , тогда: - кинематическая передаточная функция первого порядка; - кинематическая передаточная функция второго порядка. Но, и 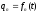, следовательно: - обобщенная скорость выходного звена; - обобщенное ускорение выходного звена.

Таким образом, функция положения и кинематические передаточные функции первого и второго порядка позволяют иметь полную информацию о кинематике механизма при различных законах движения входных звеньев. Они могут быть получены двумя способами: непосредственным дифференцированием функции положения или из решения системы линейных алгебраических уравнений, получаемой в результате дифференцирования системы уравнений связей механизма по независимой обобщенной координате. Так, дифференцируя систему (13) по , получим:

(14)

или в матричной форме:

.

Очевидно:

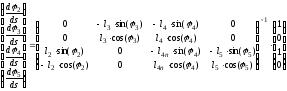
или:

, . (15)

Решение системы (15) единственно, если определитель матрицы коэффициентов отличен от нуля, в противном случае возможны два варианта: либо система имеет бесконечное множество решений, либо не имеет их вообще. Это означает, что при некоторых значениях независимой обобщенной координаты механизм приобретает дополнительные подвижности и его движение неоднозначно или он вообще не существует. В рассматриваемом примере имеем:

. (16)

Теперь, например, при и ¹³, получим: .

Из этого следует, что при , т.е., когда шатун 3 совпадет по направлению с коромыслом 4 - механизм мгновенно приобретает дополнительную подвижность и движения его звеньев однозначно не определяются заданием значения независимой обобщенной координаты ¹⁴.

Система линейных алгебраических уравнений для определения кинематических передаточных функций второго порядка имеет такую же матрицу коэффициентов, как и система (14), в чем можно легко убедиться продифференцировав ее по независимой обобщенной координате .