8.3. Группы: определение и примеры

Непустое множество G с одной бинарной алгебраической опера-цией называется группой, если выполняются следующие условия:

1. операция в G ассоциативна;

2. в G существует единичный элемент е: еа=ае=а для всех aG;

3. для каждого элемента a существует обратный ему элемент а^-1: aa^-1=a^-1a=e.

Иными словами, моноид G, все элементы которого обратимы, называется группой.

Если операция в G коммутативна, то группа называется коммутативной или абелевой.

Подмножество HG называется подгруппой в G, если ему принадлежит единичный элемент е, для любых элементов h₁, h₂H выполняется h₁h₂H, т. е. Н замкнуто относительно операции, и для любого hH выполняется h^-1H Подгруппа HG называется собственной, если Н≠е и H≠G.

Примеры.

1. Множество целых чисел образует группу целых чисел относительно операции сложения (Z, +, 0). Эта группа коммутативна. Аналогично множество рациональных и действительных чисел образует соответственно группы относительно сложения (Q, +, 0) и (R; +, 0). Подмножество четных чисел образует подгруппу. Подмножество нечетных чисел не образует подгруппу, так как операция сложения выводит из этого множества.

2. Множество целых чисел не образует группу относительно умножения, так как может не существовать обратного элемента. Все отличные от нуля рациональные числа и действительные числа образуют группы относительно умножения, причем коммутативные. Положительные рациональные и положительные действительные числа образуют подгруппы этих групп.

3. Пусть X—произвольное множество, S(X) — множество всех биективных отображений X в себя. Тогда S(X) — группа относительно операции композиции О. Она называется группой преобразований.

4. Рассмотрим множество М_п квадратных матриц порядка п с определителем, отличным от нуля. Это некоммутативная группа (M_n, •, Е) относительно операции умножения матриц, поскольку каждый элемент имеет обратный — обратную матрицу. Подмножество матриц с определителем, равным 1, образует подгруппу, так как

det E=l; det A = l; det B=1→det AB = l; det A = l→det A^-1=l.

5. Множество элементов {x₁, x₂, х₃, х₄} относительно операции, определенной таблицей Кэли (см. табл. 8.1.),— группа. Для элемента х₂, например, обратным является элемент x₄.

8.4. Циклические группы. Группы подстановок

Пусть G —группа, H и F — ее подгруппы. Тогда пересечение D=H∩F непустое, поскольку оно содержит единичный элемент. D также является подгруппой группы G. Действительно, если элементы а и b принадлежат D, то их произведение и обратные им элементы содержатся как в H, так и в F, и поэтому также принадлежат D. Аналогично доказывается и следующее утверждение.

Теорема. Пересечение любого множества подгрупп группы G само является подгруппой этой группы.

Пусть S — произвольное непустое подмножество группы G. Рассмотрим всевозможные подгруппы G, которые содержат S в качестве подмножества. Одной из них будет, в частности, сама группа G. В силу теоремы пересечение всех таких подгрупп будет подгруппой G, которая называется подгруппой, порожденной множеством S, и обозначается <S>.

Если множество S состоит из одного элемента а, то порожденная им подгруппа <a> называется циклической подгруппой, порожденной элементом а.

Обозначим (a^-1)^k=a^-k.

Теорема. Циклическая подгруппа <а>, порожденная элементом а, состоит из всех степеней элемента а.

Заметим, что все степени элемента а принадлежат подгруппе <а> и для любого целого k (a^-1)^-k=a^k. С другой стороны, эти степени сами составляют подгруппу, так как a^maⁿ=a^m+n, a°=e, а обратным элементу а^п является элемент а^-n. Действительно, нетрудно доказать, что для любых целых m и п

a^maⁿ=a^m+n ; (а^т)^п=а^тп.

Для натуральных т и п это следует из свойств операций. Если m<0, n<0, то

a^maⁿ =(a^–1) ^–m(a^–1)^-n=(a^–1)^-(m+n)= a^m+n

Если m<0, n>0, то

a^maⁿ =(a^–1)^-maⁿ=(a^-1…a^-1)(a…a)=

-m раз n раз

Случай m>0, n>0 аналогичен предыдущему. Доказательство второго равенства предлагается провести самостоятельно.

Группа, совпадающая с одной из своих циклических подгрупп (т. е. состоящая из степеней одного из своих элементов), называется циклической, а элемент, из степеней которого состоит циклическая группа,— ее образующим. Всякая циклическая группа коммутативна.

Пример.

1. Группа (Z, +, 0) — циклическая. Ее образующий элемент — число 1. Это бесконечная группа. В качестве ее образующего можно взять число 1.

2. Рассмотрим множество квадратных матриц второго порядка с целыми элементами и определителем, равным 1. Это группа относительно операции умножения матриц (покажите сами). Тогда матрица А = порождает бесконечную циклическую подгруппу, при этом Aⁿ=.

Теорема. Всякая подгруппа циклической группы сама циклическая.

Действительно, пусть G = <a>—циклическая группа с образующим элементом а и Н — подгруппа G, отличная от единичной. Предположим, что положительная наименьшая степень элемента а, содержащаяся в H, есть a^k. Тогда < a^k > H. Допустим, что в Н содержится элемент а^l, где l≠0 и l не делится на k. Тогда, если d — наибольший общий делитель чисел k и l, существуют такие целые числа и и v, что ku+lv=d, и, следовательно, в H должен содержаться элемент (a^k)^u(a^l)^v=a^d. Но так как d<.k, то приходим к противоречию относительно выбора элемента a^k. Следовательно, H=<a^k>.

Пусть G — произвольная группа, a — некоторый ее элемент. Если все степени элемента а различны, то говорят, что элемент а имеет бесконечный порядок. Если для некоторых т и п, где т≠п, а^т=а^п, то a^\m-n\=е, т. е. существуют положительные степени элемента а, равные единичному элементу. Пусть q — наименьшее положительное число, для которого а^q=е. Тогда говорят, что a — элемент конечного порядка q.

Рассмотрим еще один важный класс групп.

Пусть X—-конечное множество из n элементов. Группа всех биекций множества X в себя называется симметрической группой степени п. Без ограничения общности можно считать, что множество X состоит из элементов {1, 2, ..., n}. Каждая биекция :ХХ называется подстановкой и записывается символом , где под элементом k, 1kn, записан его образ . Произведением подстановок является композиция отображений . Например, для подстановок

и имеем . В то же время , так что . Единичную (тождественную) подстановку обозначаем е=. Симметрическая группа степени п обозначается S_n и содержит n! элементов.

Пример. Группа S₃ состоит из следующих шести элементов:

a₁=e=, a₂=, a₃=, a₄=, a₅=, a₆=

Для подстановки имеем

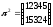, =e.

Тогда (2) =4, ² (2) =5, (2) =2.

В подстановке элементы 1 и 3 остаются на месте, элемент 2 переходит в 4, элемент 4 — в 5, а элемент 5 — снова в 2. Такая подстановка называется циклом (245) длины 3. Этот же цикл можно записать и так: (452), (524).

В общем случае подстановка , перемещающая элементы j₁, j₂,…,j_k так, что (т. е. где k — наименьшее число, обладающее этим свойством), и оставляющая на месте остальные элементы, называется циклом длины k и обозначается (j₁,…,j_k). Циклы называются независимыми, если любые два из них не имеют общих переставляемых элементов.

Теорема. Каждая подстановка в S_n является произведением независимых циклов. Разложение подстановки в произведение циклов длины 2 определено однозначно с точностью до порядка циклов.

Два элемента i и j множества X называются эквивалентными относительно подстановки , если j= для некоторого целого числа s. Введенное отношение есть отношение эквивалентности на множестве X. Оно разбивает множество X на классы эквивалентности по этому отношению:. Каждый элемент iпринадлежит одному и только одному классу X_l, причем множество X_l состоит из образов элемента i при действии степеней подстановки где k_l – количество элементов в X_l. Множество X_l часто называют . В каждом классе эквивалентности X_r выберем по одному представителю i_r и подставим ему в соответствие цикл соответствующей длины k_r. Любой элемент, не принадлежащий X_r, остается на месте при действии степеней . Тогда подстановка есть произведение циклов

(8.4.1.)

Замечание. Если цикл имеет длину 1, то он действует как тождественная подстановка, Такие циклы в записи можно опускать, например:

=(156)(38)(47)(2)=(156)(38)(47).

Докажем единственность. Пусть

(8.4.2.)

есть разложение, отличное от 8.4.1; i― символ, не остающийся на месте при действии подстановки . Тогда для одного и только одного цикла из разложения (8.4.1) и для одного и только одного цикла из разложения (8.4.2) . Для каждого k =0, 1, 2, ... имеем . Поскольку цикл однозначно определяется действием подстановки на символ i, не остающийся на месте, то . Аналогично доказываются совпадения и остальных циклов разложений (8.4.1) и (8.4.2).

Цикл длины 2 называется транспозицией. Любой цикл можно записать в виде произведения транспозиций, например:

(1 2...t-1 t)=(1 t)(1 t-1)...(1 3)(1 2).

Тогда из теоремы вытекает

Следствие. Каждая подстановка в S_n является произведением транспозиций.

Пример. В группе S₄ (123)=(13) (12)=(23) (13)=(13) (24) (12) (14).

Разложение в произведение транспозиций не является единственным.

Можно доказать, что если — разложение в произведение транспозиций, то число .=(-1)^k, называемое четностью подстановки , не зависит от способа разложения и

(8.4.3)

для любых двух подстановок и .

Подстановка называется четной, если , и нечетной, если . Все транспозиции – нечетные подстановки.

Множество четных подстановок степени n образуют подгруппу A_n, которая называется знакопеременной. Действительно, согласно (8.4.3), поскольку Множество нечетных подстановок не образует группу, так как произведение двух нечетных подстановок есть четная подстановка.