- •Оглавление
- •Глава I. Алгебра матриц
- •1.1. Матрицы. Основные определения
- •1.2. Действия над матрицами
- •1.3. Задания для самостоятельной работы по главе 1
- •Глава 2. Определители
- •2.1. Перестановки и подстановки
- •2.2. Определители и их свойства
- •2.3. Миноры и алгебраические дополнения
- •2.4. Вычисление определителей n-го порядка
- •2.5. Задания для самостоятельной работы по главе 2
- •Глава 3. Алгебра матриц (продолжение)
- •3.1. Обратная матрица
- •3.2. Ранг матрицы
- •3.3. Линейная зависимость и независимость строк матрицы
- •3.4. Многочленные матрицы
- •3.5. Задания для самостоятельной работы по главе 3
- •Глава 4. Решение системы линейных уравнений
- •4.1. Система линейных уравнений
- •4.2. Методы решения системы n линейных уравнений с n неизвестными
- •4.3. Теорема Кронекера-Капелли
- •4.4. Метод Жордана-Гаусса
- •4.5. Однородные системы линейных уравнений
- •4.6. Задания для самостоятельной работы по главе 4
- •Глава 5. Векторные пространства
- •5.1. Понятие векторного пространства
- •5.2. Линейная зависимость и независимость векторов
- •5.3. Базис векторного пространства
- •5.4. Изоморфизм векторных пространств
- •5.5. Преобразование координат при изменении базиса
- •5.6. Евклидово пространство
- •5.7. Ортогональные преобразования
- •5.8. Выпуклые множества
- •5.9. Задания для самостоятельной работы по главе 5
- •Глава 6. Линейные операторы
- •6.1. Определение линейного оператора
- •6.2. Характеристический многочлен и характеристическое уравнение
- •6.3. Собственный вектор и собственное число линейного оператора
- •6.4. Задания для самостоятельной работы по главе 6
- •Глава 7. Квадратичные формы
- •7.1. Определение квадратичной формы
- •7.2. Линейное преобразование переменных в квадратичной форме
- •7.3. Ортогональное преобразование квадратичной формы к каноническому виду
- •7.4. Положительно определенные квадратичные формы
- •7.5. Задания для самостоятельной работы по главе 7
- •Глава 8. Элементы общей алгебры
- •8.1. Алгебраические операции
- •8.2. Полугруппы и моноиды
- •8.3. Группы: определение и примеры
- •8.4. Циклические группы. Группы подстановок
- •8.5. Кольца: определение, свойства, примеры
- •8.6. Поле
- •8.7. Задания для самостоятельной работы по главе 8
- •Глава 9. Элементы теории чисел
- •9.1. Наибольший общий делитель
- •9.2. Наименьшее общее кратное
- •9.3. Простые числа
- •9.4. Сравнения и классы вычетов
- •9.5. Функция Эйлера
- •9.6. Функция Мебиуса
- •9.7. Задания для самостоятельной работы по главе 9
- •Список литературы
6.3. Собственный вектор и собственное число линейного оператора
Пусть
в пространстве
![]() задан линейный оператор
задан линейный оператор
![]() .
.
Определение.
Ненулевой вектор
![]() ,
удовлетворяющий соотношению
,
удовлетворяющий соотношению
![]() ,
называется собственным вектором, а
соответствующее число
,
называется собственным вектором, а
соответствующее число
![]() - собственным значением оператора
- собственным значением оператора
![]() .
.
Из
данного определения следует, что образом
собственного вектора
![]() является коллинеарный ему вектор
является коллинеарный ему вектор
![]() .
.
Отметим
некоторые свойства собственных векторов
оператора
![]() .
.
-
Каждому собственному вектору соответствует единственное собственное число. Предположим обратное: пусть собственному вектору
 оператора
оператора
 соответствуют два собственных числа
соответствуют два собственных числа
 .
Это значит, что
.
Это значит, что
![]() ,
,
![]() .
.
Но отсюда следует, что

Так
как по условию
![]() - ненулевой вектор, то
- ненулевой вектор, то
![]() .
.
-
Если
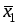 и
и
 - собственные векторы оператора
- собственные векторы оператора
 с одним и тем же собственным числом
с одним и тем же собственным числом
 ,
то их сумма
,
то их сумма
 также является собственным вектором
оператора
также является собственным вектором
оператора
 с собственным числом
с собственным числом
 .
Действительно, так как
.
Действительно, так как
 и
и
 ,
то
,
то
![]() .
.
-
Если
 - собственный вектор оператора
- собственный вектор оператора
 с собственным числом
с собственным числом
 ,
то любой вектор
,
то любой вектор
 ,
коллинеарный вектору
,
коллинеарный вектору
 ,
также является собственным вектором
оператора
,
также является собственным вектором
оператора
 с тем же самым собственным числом
с тем же самым собственным числом
 .
.
Действительно,
![]() .
.
Таким
образом, каждому собственному числу
![]() соответствует бесчисленное множество
коллинеарных собственных векторов. Из
свойств 2 и 3 следует, что множество
собственных векторов оператора
соответствует бесчисленное множество
коллинеарных собственных векторов. Из
свойств 2 и 3 следует, что множество
собственных векторов оператора
![]() ,
соответствующих одному и тому же
собственному числу, образует пространство,
которое является подпространством
пространства
,
соответствующих одному и тому же
собственному числу, образует пространство,
которое является подпространством
пространства
![]() .
.
Докажем теорему о существовании собственного вектора.
Теорема.
В комплексном линейном пространстве
![]() каждый линейный оператор
каждый линейный оператор
![]() имеет, по крайней мере, один собственный
вектор.
имеет, по крайней мере, один собственный
вектор.
Доказательство.
Пусть
![]() - линейный оператор, заданный в пространстве
- линейный оператор, заданный в пространстве
![]() ,
а
,
а
![]() - собственный вектор этого оператора с
собственным числом
- собственный вектор этого оператора с
собственным числом
![]() ,
т.е.
,
т.е.
![]() .
Выберем произвольный базис
.
Выберем произвольный базис
![]() и обозначим координаты вектора
и обозначим координаты вектора
![]() в этом базисе через
в этом базисе через
![]() .
Тогда, если
.
Тогда, если
![]() - матрица оператора
- матрица оператора
![]() в базисе
в базисе
![]() ,
то, записывая соотношение в матричной
форме, получим
,
то, записывая соотношение в матричной
форме, получим
|
где
|
(6.3.1) |
В координатной форме матричное уравнение (6.3.1) имеет вид
|
|
(6.3.2) |
Для
отыскания собственного вектора необходимо
найти ненулевые решения системы (6.3.2),
которые существуют тогда и только тогда,
когда определитель системы равен нулю,
т.е. когда
![]() .
Отсюда следует, что собственное число
линейного оператора
.
Отсюда следует, что собственное число
линейного оператора
![]() является его характеристическим числом,
которое всегда существует. Подставляя
это число в систему (6.3.2), найдет ненулевое
решение этой системы, которое определяет
искомый собственный вектор. Теорема
доказана.
является его характеристическим числом,
которое всегда существует. Подставляя
это число в систему (6.3.2), найдет ненулевое
решение этой системы, которое определяет
искомый собственный вектор. Теорема
доказана.
Из
данной теоремы следует, что нахождение
собственного числа линейного оператора
![]() и соответствующего ему собственного
вектора
и соответствующего ему собственного
вектора
![]() сводится к решению характеристического
уравнения
сводится к решению характеристического
уравнения
![]() .
Пусть
.
Пусть
![]() - различные корни характеристического
уравнения. Подставив какой-нибудь корень
- различные корни характеристического
уравнения. Подставив какой-нибудь корень
![]() в систему (6.3.2), найдем все ее линейно
независимые решения, которые и определяют
собственные векторы, соответствующие
собственному числу
в систему (6.3.2), найдем все ее линейно
независимые решения, которые и определяют
собственные векторы, соответствующие
собственному числу
![]() .
Если ранг матрицы
.
Если ранг матрицы
![]() равен r
и r<n,
то существует k=n-r
линейно независимых собственных
векторов, отвечающих корню.
равен r
и r<n,
то существует k=n-r
линейно независимых собственных
векторов, отвечающих корню.
Пример.
Найти собственные векторы линейного
оператора
![]() ,
заданного матрицей
,
заданного матрицей
 .
.
Решение. Составим характеристическое уравнение
 ,
,
или
![]() откуда
откуда
![]() .
.
Подставляем
корни
![]() в систему (6.3.1). Найдем собственные
векторы оператора
в систему (6.3.1). Найдем собственные
векторы оператора
![]() .
.
При
![]() имеем
имеем
![]()
 .
.
Получим
однородную систему трех линейных
уравнений, из которых только одно (любое)
является линейно независимым. Общее
решение системы имеет вид
![]() .
Найдем два линейно независимых решения:
.
Найдем два линейно независимых решения:
![]() .
.
Тогда
собственные векторы, соответствующие
собственным значениям
![]() ,
имеют вид
,
имеют вид
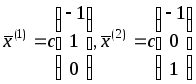 ,
,
где с – произвольное действительное число, отличное от нуля.
При
![]() имеем
имеем
 .
.
Общее решение данной системы имеет вид
![]()
Собственный
вектор, соответствующий собственному
значению
![]() ,
равен
,
равен
 .
.
Теорема.
Пусть
собственные значения
![]() оператора
оператора
![]() попарно различны. Тогда отвечающие им
собственные векторы
попарно различны. Тогда отвечающие им
собственные векторы
![]() линейно независимы.
линейно независимы.
Доказательство.
Используем метод индукции по числу
переменных. Так как
![]() - ненулевой вектор, то при p=1
утверждение теоремы справедливо.
- ненулевой вектор, то при p=1
утверждение теоремы справедливо.
Пусть
утверждение теоремы справедливо для
m<p
векторов
![]() .
Присоединим к этим векторам вектор
.
Присоединим к этим векторам вектор
![]() и допустим, что имеет место равенство
и допустим, что имеет место равенство
|
|
(6.3.3) |
Используя свойство линейного оператора, получим
|
|
(6.3.4) |
Так
как
![]() ,
-собственные векторы, то
,
-собственные векторы, то
![]() и поэтому равенство (6.3.4) можно переписать
следующим образом:
и поэтому равенство (6.3.4) можно переписать
следующим образом:
|
|
(6.3.5) |
Умножим
(6.3.3) на
![]() и вычтем из (6.3.5), получим
и вычтем из (6.3.5), получим
|
|
(6.3.6) |
По
условию все
![]() ,
различны, поэтому
,
различны, поэтому
![]() .
Система векторов
.
Система векторов
![]() - линейно независимая. Поэтому из (6.3.6)
следует, что
- линейно независимая. Поэтому из (6.3.6)
следует, что
![]() .
Тогда из (6.3.3) и из условия, что
.
Тогда из (6.3.3) и из условия, что
![]() - собственный вектор (
- собственный вектор (![]() ),
получаем
),
получаем
![]() .
Это означает, что
.
Это означает, что
![]() - система линейно независимых векторов.
Индукция проведена. Теорема доказана.
- система линейно независимых векторов.
Индукция проведена. Теорема доказана.
Следствие:
если все собственные значения
![]() попарно различны, то отвечающие им
собственные векторы
попарно различны, то отвечающие им
собственные векторы
![]() образуют базис пространства
образуют базис пространства
![]() .
.
Теорема.
Если в
качестве базиса пространства
![]() принять n
линейно независимых собственных
векторов, то оператору
принять n
линейно независимых собственных
векторов, то оператору
![]() в этом базисе соответствует диагональная
матрица
в этом базисе соответствует диагональная
матрица
 .
.
Доказательство.
Рассмотрим произвольный вектор
![]() и базис, составленный из собственных
векторов
и базис, составленный из собственных
векторов
![]() этого пространства. Тогда
этого пространства. Тогда
![]() ,
где
,
где
![]() - координаты вектора
- координаты вектора
![]() в базисе
в базисе
![]() .
.
Применяя
к вектору
![]() оператор
оператор
![]() ,
получим
,
получим
![]() или
или
 .
.
Так
как
![]() ,
- собственный вектор, то
,
- собственный вектор, то
![]() .
.
Тогда
|
|
(6.3.7) |
Из (6.3.7) имеем
|
…………
|
(6.3.8) |
Равенства
(6.3.8) означают, что матрица линейного
оператора
![]() в базисе
в базисе
![]() имеет вид
имеет вид
 .
.
Теорема доказана.
Определение.
Линейный оператор
![]() в пространстве
в пространстве
![]() называется оператором простой структуры,
если он имеет n
линейно независимых собственных
векторов.
называется оператором простой структуры,
если он имеет n
линейно независимых собственных
векторов.
Очевидно,
что операторы простой структуры, и
только они, имеют диагональные матрицы
в некотором базисе. Этот базис может
быть составлен лишь из собственных
векторов оператора
![]() .
Действие любого оператора простой
структуры всегда сводится к «растяжению»
координат вектора в данном базисе.
.
Действие любого оператора простой
структуры всегда сводится к «растяжению»
координат вектора в данном базисе.