
- •Оглавление
- •Глава I. Алгебра матриц
- •1.1. Матрицы. Основные определения
- •1.2. Действия над матрицами
- •1.3. Задания для самостоятельной работы по главе 1
- •Глава 2. Определители
- •2.1. Перестановки и подстановки
- •2.2. Определители и их свойства
- •2.3. Миноры и алгебраические дополнения
- •2.4. Вычисление определителей n-го порядка
- •2.5. Задания для самостоятельной работы по главе 2
- •Глава 3. Алгебра матриц (продолжение)
- •3.1. Обратная матрица
- •3.2. Ранг матрицы
- •3.3. Линейная зависимость и независимость строк матрицы
- •3.4. Многочленные матрицы
- •3.5. Задания для самостоятельной работы по главе 3
- •Глава 4. Решение системы линейных уравнений
- •4.1. Система линейных уравнений
- •4.2. Методы решения системы n линейных уравнений с n неизвестными
- •4.3. Теорема Кронекера-Капелли
- •4.4. Метод Жордана-Гаусса
- •4.5. Однородные системы линейных уравнений
- •4.6. Задания для самостоятельной работы по главе 4
- •Глава 5. Векторные пространства
- •5.1. Понятие векторного пространства
- •5.2. Линейная зависимость и независимость векторов
- •5.3. Базис векторного пространства
- •5.4. Изоморфизм векторных пространств
- •5.5. Преобразование координат при изменении базиса
- •5.6. Евклидово пространство
- •5.7. Ортогональные преобразования
- •5.8. Выпуклые множества
- •5.9. Задания для самостоятельной работы по главе 5
- •Глава 6. Линейные операторы
- •6.1. Определение линейного оператора
- •6.2. Характеристический многочлен и характеристическое уравнение
- •6.3. Собственный вектор и собственное число линейного оператора
- •6.4. Задания для самостоятельной работы по главе 6
- •Глава 7. Квадратичные формы
- •7.1. Определение квадратичной формы
- •7.2. Линейное преобразование переменных в квадратичной форме
- •7.3. Ортогональное преобразование квадратичной формы к каноническому виду
- •7.4. Положительно определенные квадратичные формы
- •7.5. Задания для самостоятельной работы по главе 7
- •Глава 8. Элементы общей алгебры
- •8.1. Алгебраические операции
- •8.2. Полугруппы и моноиды
- •8.3. Группы: определение и примеры
- •8.4. Циклические группы. Группы подстановок
- •8.5. Кольца: определение, свойства, примеры
- •8.6. Поле
- •8.7. Задания для самостоятельной работы по главе 8
- •Глава 9. Элементы теории чисел
- •9.1. Наибольший общий делитель
- •9.2. Наименьшее общее кратное
- •9.3. Простые числа
- •9.4. Сравнения и классы вычетов
- •9.5. Функция Эйлера
- •9.6. Функция Мебиуса
- •9.7. Задания для самостоятельной работы по главе 9
- •Список литературы
Международный консорциум «Электронный университет»
Московский государственный университет экономики, статистики и информатики
Евразийский открытый институт
Балюкевич Э.Л.
Романников А.Н.
Алгебра и теория чисел
Учебное пособие
Москва, 2008
УДК 51
ББК 22.143
А 535
Балюкевич Э.Л. Романников А.Н. Алгебра и теория чисел // Московский государственный университет экономики, статистики и информатики. М., 2008. – 136 с.
Балюкевич Э.Л., 2008 г.
Романников А.Н., 2008 г.
Московский государственный университет экономики, статистики и информатики, 2008 г.
Оглавление
ГЛАВА I. Алгебра матриц 6
1.1. Матрицы. Основные определения 6
1.2. Действия над матрицами 7
1.3. Задания для самостоятельной работы по главе 1 10
ГЛАВА 2. ОПРЕДЕЛИТЕЛИ 12
2.1. Перестановки и подстановки 12
2.2. Определители и их свойства 13
2.3. Миноры и алгебраические дополнения 18
2.4. Вычисление определителей n-го порядка 20
2.5. Задания для самостоятельной работы по главе 2 23
ГЛАВА 3. АЛГЕБРА МАТРИЦ (ПРОДОЛЖЕНИЕ) 26
3.1. Обратная матрица 26
3.2. Ранг матрицы 27
3.3. Линейная зависимость и независимость строк матрицы 30
3.4. Многочленные матрицы 35
3.5. Задания для самостоятельной работы по главе 3 42
ГЛАВА 4. РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ 45
4.1. Система линейных уравнений 45
4.2. Методы решения системы n линейных уравнений с n неизвестными 46
4.3. Теорема Кронекера-Капелли 49
4.4. Метод Жордана-Гаусса 52
4.5. Однородные системы линейных уравнений 61
4.6. Задания для самостоятельной работы по главе 4 65
ГЛАВА 5. ВЕКТОРНЫЕ ПРОСТРАНСТВА 68
5.1. Понятие векторного пространства 68
5.2. Линейная зависимость и независимость векторов 70
5.3. Базис векторного пространства 73
5.4. Изоморфизм векторных пространств 76
5.5. Преобразование координат при изменении базиса 77
5.6. Евклидово пространство 80
5.7. Ортогональные преобразования 88
5.8. Выпуклые множества 89
5.9. Задания для самостоятельной работы по главе 5 93
ГЛАВА 6. ЛИНЕЙНЫЕ ОПЕРАТОРЫ 95
6.1. Определение линейного оператора 95
6.2. Характеристический многочлен и характеристическое уравнение 98
6.3. Собственный вектор и собственное число линейного оператора 102
6.4. Задания для самостоятельной работы по главе 6 108
ГЛАВА 7. КВАДРАТИЧНЫЕ ФОРМЫ 110
7.1. Определение квадратичной формы 110
7.2. Линейное преобразование переменных в квадратичной форме 111
7.3. Ортогональное преобразование квадратичной формы к каноническому виду 117
7.4. Положительно определенные квадратичные формы 120
7.5. Задания для самостоятельной работы по главе 7 123
ГЛАВА 8. ЭЛЕМЕНТЫ ОБЩЕЙ АЛГЕБРЫ 125
8.1. Алгебраические операции 125
8.2. Полугруппы и моноиды 127
8.3. Группы: определение и примеры 130
8.4. Циклические группы. Группы подстановок 131
8.5. Кольца: определение, свойства, примеры 136
8.6. Поле 137
8.7. Задания для самостоятельной работы по главе 8 139
ГЛАВА 9. ЭЛЕМЕНТЫ ТЕОРИИ ЧИСЕЛ 140
9.1. Наибольший общий делитель 141
9.2. Наименьшее общее кратное 142
9.3. Простые числа 142
9.4. Сравнения и классы вычетов 143
9.5. Функция Эйлера 146
9.6. Функция Мебиуса 146
9.7. Задания для самостоятельной работы по главе 9 147
Список литературы 149
Глава I. Алгебра матриц
1.1. Матрицы. Основные определения
Матрицей
А=(![]() )
)![]() называется прямоугольная таблица чисел,
содержащая m
строк и n
столбцов:
называется прямоугольная таблица чисел,
содержащая m
строк и n
столбцов:
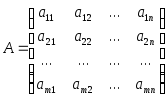
Числа
![]() (
(![]() ),
составляющие данную матрицу, называются
её элементами; i
– номер строки матрицы, j
– номер столбца.
),
составляющие данную матрицу, называются
её элементами; i
– номер строки матрицы, j
– номер столбца.
Если
m=n,
то матрица называется квадратной порядка
n.
Например,
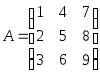 – квадратная матрица третьего порядка.
Про элементы
– квадратная матрица третьего порядка.
Про элементы
![]() такой матрицы говорят, что они стоят на
главной диагонали.
такой матрицы говорят, что они стоят на
главной диагонали.
Треугольная матрица – квадратная матрица, у которой все элементы, стоящие по одну из сторон главной диагонали, равны нулю:
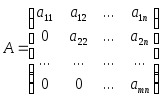 ,
например,
,
например,
 – треугольная матрица третьего порядка
– треугольная матрица третьего порядка
Квадратная матрица вида

называется
диагональной матрицей. Диагональные
матрицы, в которых все диагональные
элементы равны, т.е.
![]() ,
,
![]() ,
называются скалярными матрицами.
,
называются скалярными матрицами.
Если
![]()
![]() ,
то скалярная матрица называется единичной
и обозначается буквой Е,
т.е.:
,
то скалярная матрица называется единичной
и обозначается буквой Е,
т.е.:
 .
.
Например, матрицы А, B, E являются соответственно диагональной, скалярной и единичной третьего порядка.
 ,
,
 ,
,
 .
.
Симметрической
называется квадратная матрица, у которой
элементы, расположенные симметрично
относительно главной диагонали, равны,
т.е.
![]()
Например,
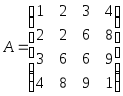 - симметрическая матрица четвертого
порядка.
- симметрическая матрица четвертого
порядка.
Матрица, состоящая из одной строки, называется вектором-строкой, а матрица, состоящая из одного столбца, – вектором-столбцом.
Матрица,
все элементы которой равны нулю,
называется нулевой матрицей и обозначается
О.
Например, О![]() - нулевая
матрица размера два на три.
- нулевая
матрица размера два на три.
