
- •Глава 4 Аналитическая геометрия на плоскости
- •§ 1. Параллельный перенос осей координат
- •§ 2. Различные виды уравнений прямой на плоскости
- •§3. Кривые второго порядка
- •1. Окружность.
- •Решение практических задач по теме: «Различные виды уравнений прямой на плоскости»
- •Решение практических задач по теме: «Кривые второго порядка»
- •Примеры для самостоятельного решения
Решение практических задач по теме: «Различные виды уравнений прямой на плоскости»
П р и м е р 1. Построить прямые: а) 3 x – 2 y – 6 = 0;
б) 2 x – 5 y = 0;
в) 2 y – 1 = 0;
г) 3 x + 2 = 0;
д) 5 y = 0.
Решение. а) прямая пересекает обе координатные оси, т. к. в ее уравнении коэффициенты при текущих координатах х и у и свободный член не равны нулю. Приведем данное уравнение к уравнению в отрезках. Для этого свободный член перенесем вправо и обе части уравнения разделим на 6, т. е.
3 x
– 2 y
= 6
![]() или
или
![]() .
.
С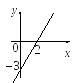 равнивая
полученное уравнение с уравнением (5),
замечаем, что а
= 2, а b
= – 3. На оси Ох
от начала координат откладываем две
единицы в положительном направлении,
на оси Оу
три единицы в отрицательном направлении.
Через полученные точки проводим прямую.
равнивая
полученное уравнение с уравнением (5),
замечаем, что а
= 2, а b
= – 3. На оси Ох
от начала координат откладываем две
единицы в положительном направлении,
на оси Оу
три единицы в отрицательном направлении.
Через полученные точки проводим прямую.
б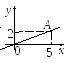 )
прямая проходит через начало координат,
т. к. ее уравнение не содержит свободного
члена. Для построения найдем еще одну
точку на этой прямой. Дадим одной из
переменных в заданном уравнении
произвольное значение, например х
= 5 и из уравнения 2∙5 – 5∙у
= 0 определим 5∙у
= 10, у
= 2. Через точки А
(5; 2) и О
(0; 0) проводим прямую.
)
прямая проходит через начало координат,
т. к. ее уравнение не содержит свободного
члена. Для построения найдем еще одну
точку на этой прямой. Дадим одной из
переменных в заданном уравнении
произвольное значение, например х
= 5 и из уравнения 2∙5 – 5∙у
= 0 определим 5∙у
= 10, у
= 2. Через точки А
(5; 2) и О
(0; 0) проводим прямую.
в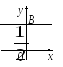 )
Прямая параллельна оси Ох,
т. к. ее уравнение не содержит текущей
координаты х.
Из уравнения прямой находим 2∙у
= 1,
)
Прямая параллельна оси Ох,
т. к. ее уравнение не содержит текущей
координаты х.
Из уравнения прямой находим 2∙у
= 1,
![]() и через точку
и через точку
![]() параллельно оси Ох
проводим прямую.
параллельно оси Ох
проводим прямую.
г )
Так как в уравнении 3∙х
+ 2 = 0 или
)
Так как в уравнении 3∙х
+ 2 = 0 или
![]() отсутствует текущая координата у,
то прямая параллельна оси Оу
и проходит через точку
отсутствует текущая координата у,
то прямая параллельна оси Оу
и проходит через точку
![]() .
.
д) Прямая 5∙у = 0 или у = 0 совпадает с осью Ох, т. к. в уравнении отсутствуют свободный член и текущая координата х.
П р и м е р 2. Написать уравнения прямых изображенных на рисунке.
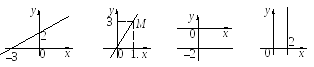
Решение. а) Найдем отрезки, отсекаемые этой прямой на осях координат. Из чертежа видно, что а = – 3, b = 2. Подставим эти значения в уравнение (5):
![]()
и после преобразований получим общее уравнение прямой
2∙х – 3∙у + 6 = 0.
б) Прямая проходит через начало координат. Ее уравнение имеет вид А∙х + В∙у = 0. Найдем коэффициенты А и В. Точка М (1; 3) лежит на этой прямой, поэтому ее коэффициенты удовлетворяют уравнению А∙х + В∙у = 0, т. е.
А∙1 + В∙3 = 0.
Отсюда следует, что А = – 3∙В.
Подставим это значение в уравнение А∙х + В∙у = 0 и получим
– 3 В х + В у = 0, – В (3 х – у) = 0.
Так как В 0, то, разделив обе части равенства на (– В), получим искомое уравнение
3 х – у = 0.
в) Прямая параллельна ос Ох, ее уравнение у = – 2.
г) Прямая параллельна оси Оу, ее уравнение х = 2.
П р и м е р 3. Составить уравнение прямой, отсекающей на оси ординат отрезок b = – 3 и образующей с положительным направлением оси абсцисс угол α = π/6.
Решение.
Находим угловой коэффициент: k
= tg
(π/6)
=
![]() .
Воспользовавшись уравнением прямой с
угловым коэффициентом, получаем
.
Воспользовавшись уравнением прямой с
угловым коэффициентом, получаем
![]() ;
освобождаясь от знаменателя и перенося
все члены в левую часть, получаем общее
уравнение прямой
;
освобождаясь от знаменателя и перенося
все члены в левую часть, получаем общее
уравнение прямой
![]() .
.
П р и м е р 4. Составить уравнение прямой, проходящей через точки А (– 1; 3) и В (2; 5).
Решение. Полагая х1 = – 1, у1 = 3, х2 = 2, у2 = 5 в уравнении (3), получаем
![]()
Итак, искомое уравнение имеет вид 2 х – 3 у + 11 = 0.
Полезно проверить, что уравнение составлено верно. Для этого достаточно показать, что координаты точек А и В удовлетворяют уравнению прямой. Действительно, равенства 2 (– 1) – 3∙3 + 11 = 0, 2∙2 – 3∙5 + 11 = 0 выполняются тождественно.
П р и м е р 5.
Определить угол между прямыми:
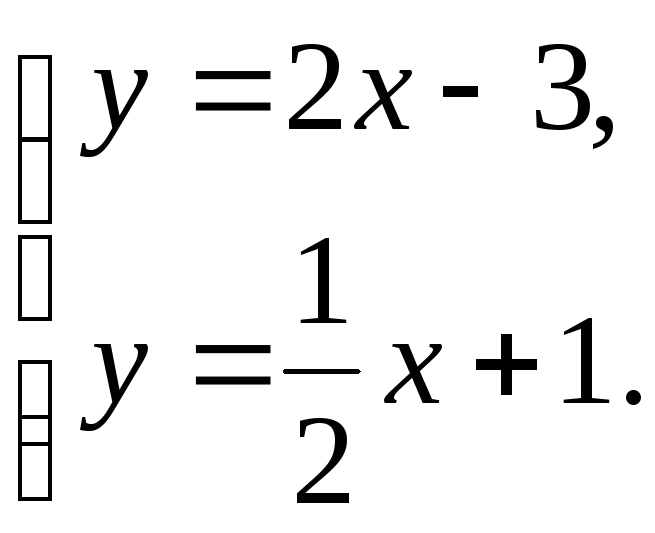
Решение.
Так как угловой коэффициент первой
прямой равен k2
= 2, а второй прямой – k1
=
![]() ,
то угол между этими прямыми найдем по
формуле
,
то угол между этими прямыми найдем по
формуле
![]() .
.
Следовательно, φ = arctg 0,75.
П р и м е р 6. Дан треугольник с вершинами А (– 2; 0), В (2; 4), С (4; 0). Написать уравнения сторон треугольника, медианы АЕ, высоты АD и найти длину медианы АЕ.
Решение. 1) Найдем уравнения прямых на которых лежат стороны треугольника, воспользовавшись уравнением прямой проходящей через две точки:
![]()
![]()
![]()
2) Чтобы найти уравнение прямой на которой лежит медиана АЕ, найдем координаты точки Е, которая является серединой отрезка ВС:
![]() ,
,
т. е. точка Е имеет координаты Е (3; 2).
Теперь найдем уравнение прямой
![]()
3) Найдем длину высоты АЕ как расстояние от точки А до точки Е:
![]() .
.
