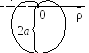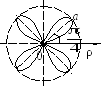- •Глава 4 Аналитическая геометрия на плоскости
- •§ 1. Параллельный перенос осей координат
- •§ 2. Различные виды уравнений прямой на плоскости
- •§3. Кривые второго порядка
- •1. Окружность.
- •Решение практических задач по теме: «Различные виды уравнений прямой на плоскости»
- •Решение практических задач по теме: «Кривые второго порядка»
- •Примеры для самостоятельного решения
§3. Кривые второго порядка
1. Окружность.
Уравнение окружности с центром в точке С (х0, у0) и радиусом R в декартовой системе координат имеет вид
(х – х0)2 + (у – у0)2 = R2. (11)
Уравнение окружности с центром в начале координат и радиусом R:
х2 + у2 = R2. (12)
Это уравнение называется каноническим (простейшим) уравнением окружности.
Параметрические уравнения окружности имеют вид
 ,
(13)
,
(13)
где t
– угол между положительным направлением
оси Ох
и радиусом
![]() текущей точки М
(х,
у)
окружности, отсчитываемый против хода
часовой стрелки.
текущей точки М
(х,
у)
окружности, отсчитываемый против хода
часовой стрелки.
В полярной системе координат окружность определяется одним из следующих уравнений:
|
1
|
|
|
2
|
4 |
|
3
|
5
|
2. Эллипс. Эллипсом с центром симметрии в начале координат О (0; 0) называется кривая, уравнение которой в прямоугольной системе координат Оху имеет вид:
![]() (14)
(14)
где a > 0 и b > 0 называются полуосями эллипса. Данное уравнение называется каноническим уравнением эллипса.
Е сли
а
> b,
то ось 2а
называется большой
осью эллипса
и лежит на оси
Ох,
а
ось 2b
–
малой осью
и лежит на оси Оу.
Точки F1
(– c;
0) и F2
(c;
0), где
сли
а
> b,
то ось 2а
называется большой
осью эллипса
и лежит на оси
Ох,
а
ось 2b
–
малой осью
и лежит на оси Оу.
Точки F1
(– c;
0) и F2
(c;
0), где
![]() ,
называются фокусами
эллипса, соответственно левым
,
называются фокусами
эллипса, соответственно левым
и правым; 2с – фокусным расстоянием. Точки с координатами (а; 0), (– а; 0), (0; b), (0; – b) называются вершинами эллипса.
Фокальное свойство эллипса
Д ля
того чтобы точка М
(х;
у)
принадлежала эллипсу (1) необходимо и
достаточно, чтобы сумма расстояний от
этой точки до фокусов эллипса F1
и F2
была постоянной и равнялась 2а,
т. е.
ля
того чтобы точка М
(х;
у)
принадлежала эллипсу (1) необходимо и
достаточно, чтобы сумма расстояний от
этой точки до фокусов эллипса F1
и F2
была постоянной и равнялась 2а,
т. е.
|M F1| + |M F2| = 2a.
Если a
< b,
то уравнение (1) определяет эллипс,
большая ось которого 2b
лежит на оси Оу,
а малая ось 2а
– на оси Ох.
Фокусы такого эллипса находятся на оси
Оу
в точках F1
(0; – c)
и F2
(0; с),
где
![]() .
Его фокальное свойство:
.
Его фокальное свойство:
|M F1| + |M F2| = 2b.
Если a = b, то каноническое уравнение эллипса примет вид х2 + у2 = а2, которое соответствует окружности радиуса а с центром в начале координат. Таким образом, окружность является частным случаем эллипса.
Параметрические уравнения эллипса имеют вид:

Е сли
центр симметрии эллипса лежит в точке
С
(х0;
у0),
то его каноническое уравнение имеет
вид:
сли
центр симметрии эллипса лежит в точке
С
(х0;
у0),
то его каноническое уравнение имеет
вид:
![]()
3. Гипербола. Гиперболой с центром в начале координат О (0; 0) называется кривая, уравнение которой в прямоугольной системе координат Оху имеет вид:
![]() .
(15)
.
(15)
г де
а
> 0 – называется действительной
полуосью и
лежит на оси Ох,
а b
> 0 – мнимой
полуосью
гиперболы и лежит на оси Оу.
Данное уравнение называется каноническим
уравнением гиперболы.
де
а
> 0 – называется действительной
полуосью и
лежит на оси Ох,
а b
> 0 – мнимой
полуосью
гиперболы и лежит на оси Оу.
Данное уравнение называется каноническим
уравнением гиперболы.
Точки F1
(– c;
0) и F2
(c;
0), где
![]() ,
называются фокусами
гиперболы, соответственно левым и
правым; 2с
– фокусным расстоянием. Точки с
координатами (а;
0) и (– а;
0) называются вершинами
гиперболы.
,
называются фокусами
гиперболы, соответственно левым и
правым; 2с
– фокусным расстоянием. Точки с
координатами (а;
0) и (– а;
0) называются вершинами
гиперболы.
Прямые
![]() называются асимптотами
гиперболы.
Прямоугольник со сторонами 2а
и 2b
называется основным прямоугольником
гиперболы.
называются асимптотами
гиперболы.
Прямоугольник со сторонами 2а
и 2b
называется основным прямоугольником
гиперболы.
Фокальное свойство гиперболы
Для того чтобы точка М (х; у) принадлежала гиперболе (2) необходимо и достаточно, чтобы разность расстояний от этой точки до фокусов гиперболы F1 и F2 по абсолютной величине была постоянной и равнялась 2а, т. е.
|M F1| – |M F2| = 2a.
Если a = b, то каноническое уравнение эллипса примет вид х2 + у2 = а2, которое соответствует окружности радиуса а с центром в начале координат. Таким образом, окружность является частным случаем эллипса.
Определение 6. Гипербола, уравнение которой имеет вид
![]()
 (16)
(16)
называется
сопряженной
гиперболе
(2). Действительная ось этой гиперболы
лежит на оси Оу
и равна 2b,
а мнимая – на оси Ох
и равна 2а.
Фокусы сопряженной гиперболы находятся
на оси Оу
в точках F1
(0; – c)
и F2
(0; с),
где
![]() .
.
Фокальное свойство гиперболы заданной уравнением (3):
|M F1| – |M F2| = 2b.
Замечание. При построении гиперболы целесообразно построить основной прямоугольник гиперболы, провести в нем диагонали и продолжить их за вершины прямоугольника.
Если а = b, то гипербола называется равносторонней.
Если центр гиперболы лежит в точке С (х0; у0), то ее каноническое уравнение имеет вид
![]() ,
,
а уравнение сопряженной гиперболы
![]()

 .
.
4. Парабола. Параболой называется кривая, уравнение которой в прямоугольной системе координат имеет вид
у2 = 2∙р∙х. (17)
где р
> 0 называется параметром параболы.
Это уравнение называется каноническим
уравнением параболы. Вершина ее лежит
в точке О
(0; 0). Точка
![]() называется фокусом, а прямая
называется фокусом, а прямая
![]() директрисой параболы.
директрисой параболы.
Ф окальное
свойство параболы
окальное
свойство параболы
Для того чтобы точка М (х; у) принадлежала параболе (4) необходимо и достаточно, чтобы расстояние от этой точки до фокуса параболы было равно расстоянию от этой же точки до директрисы параболы, т. е.
|MK| = |MF|.
Уравнения у2 = – 2∙р∙х, х2 = 2∙р∙у, х2 = – 2∙р∙у (р > 0) также определяют следующие параболы:


Если вершина параболы лежит в точке С (х0; у0), то ее каноническое уравнение примет вид:
(у – у0)2 = 2∙р∙(х – х0).
Общее уравнение кривой второго порядка
Уравнение А∙х2 + В∙х∙у + С∙у2 + D∙x + E∙y + F= 0, в котором А, В, С одновременно не равны нулю, называется общим уравнением кривой второго порядка.
В данном кратком курсе при рассмотрении общих уравнений кривых второго порядка ограничимся случаем, когда В = 0, т. е. рассмотрим уравнение кривой второго порядка без члена с произведением координат х и у:
А∙х2 + С∙у2 + D∙x + E∙y + F= 0.
Для того чтобы научиться определять какую кривую описывает данное уравнение, сформулируем теорему.
Т е о р е м а. Уравнение А∙х2 + С∙у2 + D∙x + E∙y + F = 0 всегда определяет:
– окружность, если А = С;
– эллипс, если АС > 0;
– гиперболу, если АС< 0;
– параболу, если АС = 0.
При этом возможны случаи вырождения: для эллипса (окружности) – в точку или мнимый эллипс (окружность), для гиперболы – в пару пересекающихся прямых, для параболы – в пару параллельных прямых.
Некоторые другие кривые
|
Название |
Уравнение |
К |
|
1. Астроида. |
|
|
|
2. Циклоида. |
|
|
|
3. Кардиоида. |
ρ = а (1 – cosφ). |
|
|
ρ = а (1 + cosφ). |
|
|
|
ρ = a (1 + sin φ). |
|
|
|
ρ = a (1 – sin φ). |
|
|
|
4. Лемниската Бернулли. |
ρ2 = а2sin 2φ. |
|
|
ρ2 = а2cos 2φ. |
|
|
|
5. Четырехлепестковая роза |
ρ = а соs 2φ. |
|
|
ρ = а sin 2φ. |
|
|
|
6. Трехлепестковая роза |
ρ = а соs 3φ |
|
|
ρ = а sin 3φ |
|
Таблица понятий и формул по теме «Прямая на плоскости»
|
№ |
Понятие |
Содержание, формула |
|
1. |
Угловой коэффициент прямой К. |
Тангенс угла, образованного с положительным направлением оси Ох: k = tg α |
|
2. |
Общее уравнение прямой. |
А∙х + В∙у + С = 0, где А, В, С – произвольные числа одновременно не равны нулю. |
|
3. |
Уравнение прямой с угловым коэффициентом. |
y = k∙x + b, k – угловой коэффициент прямой. |
|
4. |
Вычисление угла между прямыми y = k1∙x + b1 и y = k2∙x + b2. |
|
|
5. |
Условие параллельности двух прямых |
k1∙= k2. |
|
6. |
Условие перпендикулярности двух прямых |
k1∙k2∙=
– 1 или
|
|
7. |
Уравнение прямой, проходящей через данную точку М0 (х0; у0) с данным угловым коэффициентом. |
(у – у0) = k∙(x – x0). |
|
8. |
Уравнение прямой, проходящей через две заданные точки М1 (х1; у1) и М2 (х2; у2). |
|
|
9. |
Вычисление углового коэффициента прямой, проходящей через две заданные точки М1 (х1; у1) и М2 (х2; у2). |
|
|
10. |
Вычисление расстояния d от точки М0 (х0; у0) до прямой А∙х + В∙у + С = 0. |
|

 )
)
 )
ρ
= а
sinφ.
)
ρ
= а
sinφ. )
ρ
= а
cosφ.
)
ρ
= а
cosφ. )
ρ
= – а
sinφ.
)
ρ
= – а
sinφ. )
ρ
= – а
cosφ.
)
ρ
= – а
cosφ. ривая
ривая