
- •Белорусский национальный технический университет
- •Практикум по курсу «Каналы передачи информации»
- •Часть 1
- •Составитель и разработчик в.В.Баркалин.
- •Тема 1: Информация и ее измерение. Определения и глоссарий
- •Задания для предварительной самостоятельной подготовки
- •Учебно-исследовательское задание
- •Литература
- •Тема 2: Основные понятия теории вероятностей. Вычисление вероятностей составных событий Определения и глоссарий
- •Задания для предварительной самостоятельной подготовки
- •Литература
- •Тема 3: условные вероятности Определения и глоссарий
- •Задания для предварительной самостоятельной подготовки
- •Учебно-исследовательское задание
- •Литература
- •Тема 4: Законы распределения и числовые характеристики одномерных случайных величин Определения и глоссарий
- •Задания для предварительной самостоятельной подготовки
- •Учебно-исследовательское задание
- •Литература
- •Тема 5: Многомерные случайные величины и условные функции распределения. Определения и глоссарий
- •Задания для предварительной самостоятельной подготовки
- •Учебно-исследовательское задание
- •Литература
- •Тема 5: Многомерные случайные величины и условные функции распределения (продолжение). Задачи
- •Тема 6: -функция Дирака.
- •Тема 7: Преобразования одномерных случайных величин.
- •Тема 8: Преобразования многомерных случайных величин.
- •Учебно-исследовательское задание
- •Литература
- •Тема 9: энтропия и количество информации в дискретных системах Определения и глоссарий
- •Задания для предварительной самостоятельной подготовки
- •Учебно-исследовательское задание
- •Литература
- •Тема 10: Дискретные каналы передачи информации Определения и глоссарий
- •Задания для предварительной самостоятельной подготовки
- •Тема 11: Законы распределения случайных процессов
- •Тема 12: корреляционные функции случайных процессов
- •Тема 13: спектральные плотности случайных процессов
- •Тема 14: Непрерывные системы передачи информации
- •Учебно-исследовательское задание
- •Литература
- •Содержание
Тема 11: Законы распределения случайных процессов
Определения и глоссарий
Случайная величина, случайная функция времени, случайный процесс, 5 основных типов случайных процессов: дискретная последовательность, случайная последовательность, дискретный процесс, непрерывнозначный процесс, случайный поток, стационарные и нестационарные процессы, эргодические процессы
Задачи
-
Найти одномерную плотность гармонического случайного процесса
 с постоянными амплитудой и частотой,
начальная фаза которого равномерно
распределена в интервале
с постоянными амплитудой и частотой,
начальная фаза которого равномерно
распределена в интервале
 .
. -
Найти одномерную
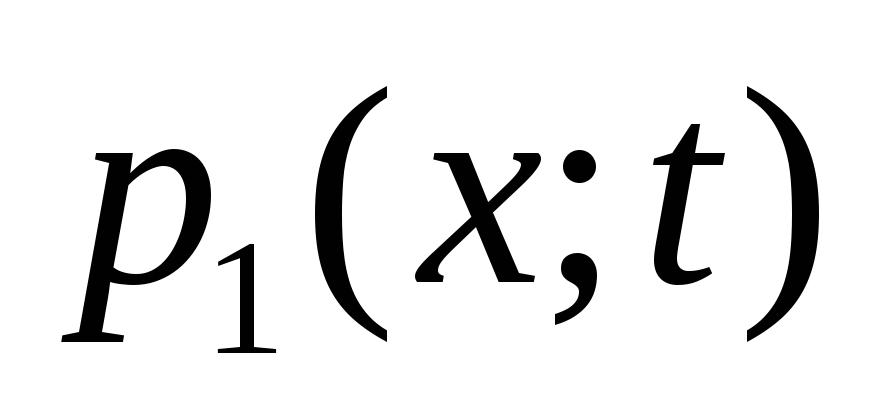 и двумерную
и двумерную
 плотности
распределения случайного процесса
плотности
распределения случайного процесса
 ,
где ω - постоянная угловая частота, α и
β - взаимно независимые гауссовские
случайные величины с нулевыми
математическими ожиданиями
,
где ω - постоянная угловая частота, α и
β - взаимно независимые гауссовские
случайные величины с нулевыми
математическими ожиданиями
 и одинаковыми дисперсиями
и одинаковыми дисперсиями
 .
. -
Найти одномерную плотность распределения вероятностей процесса
 ,
где α и β - взаимно независимые случайные
величины с плотностями распределения
,
где α и β - взаимно независимые случайные
величины с плотностями распределения
 и
и
 .
. -
Найти одномерную характеристическую функцию гауссовского процесса
 ,
имеющего плотность распределения
вероятностей
,
имеющего плотность распределения
вероятностей

-
Пользуясь понятием условной плотности распределения и одномерной плотностью распределения гармонического процесса
 с постоянной амплитудой и угловой
частотой
с постоянной амплитудой и угловой
частотой
 , найти двумерную плотность распределения
этого процесса.
, найти двумерную плотность распределения
этого процесса. -
Два гауссовских некоррелированных случайных процесса имеют заданные постоянные математические ожидания и дисперсии. Записать совместную плотность распределения вероятностей этих процессов.
-
Имеется два случайных процесса
 и
и
 ,
где α
- постоянный коэффициент. Считая
,
где α
- постоянный коэффициент. Считая
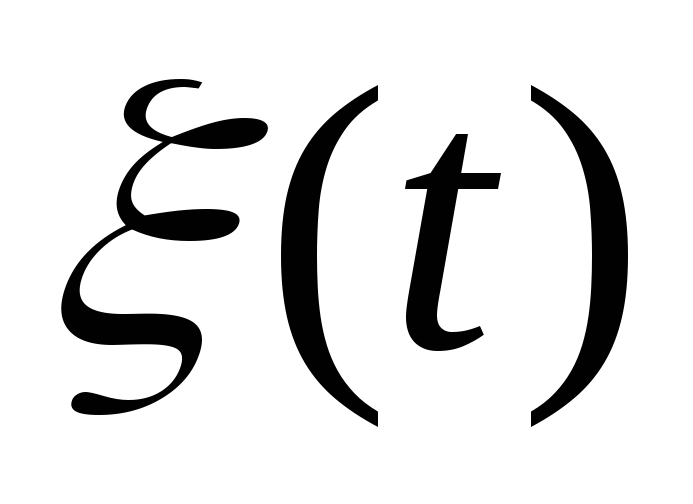 гауссовским с нулевым математическим
ожиданием и дисперсией
гауссовским с нулевым математическим
ожиданием и дисперсией
 ,
и используя определение условной
вероятности, записать совместную
плотность распределения
,
и используя определение условной
вероятности, записать совместную
плотность распределения
 и
и
 .
. -
Определить, при каких условиях процесс
 ,
у которого амплитуда и частота -
детерминированные величины, стационарен
и нестационарен в широком смысле.
,
у которого амплитуда и частота -
детерминированные величины, стационарен
и нестационарен в широком смысле. -
Случайные величины A и Φ независимы,
 ,
,
 ,
Φ равномерно
распределена в интервале
,
Φ равномерно
распределена в интервале
 .
Доказать, что случайный процесс
.
Доказать, что случайный процесс
 стационарен в широком смысле (вычислить
математическое ожидание и дисперсию
процесса
стационарен в широком смысле (вычислить
математическое ожидание и дисперсию
процесса
 ).
). -
Показать, что случайный процесс
 стационарен
в широком смысле только в том случае,
когда случайные величины X
и Y
взаимно не
коррелированы и имеют нулевые
математические ожидания и равные
дисперсии.
стационарен
в широком смысле только в том случае,
когда случайные величины X
и Y
взаимно не
коррелированы и имеют нулевые
математические ожидания и равные
дисперсии.
Учебно-исследовательское задание
-
Флуктуации энергии и числа частиц в термодинамических равновесных системах.
-
Зависимость термодинамических флуктуаций от времени.
Литература
-
В.И.Тихонов. Статистическая радиотехника. М.: Радио и Связь, 1982.
-
В.Т.Горяинов, А.Г.Журавлев, В.И.Тихонов. Статистическая радиотехника. Примеры и задачи. М.: Сов.Радио, 1980.
Практическое занятие 14.
Тема 12: корреляционные функции случайных процессов
Определения и глоссарий
Корреляционные и ковариационные функции случайных процессов, взаимные корреляционные функции, радиус корреляции, гауссов случайный процесс. Пуассоновский случайный процесс.
Задачи
-
Определить, обладает ли функция
 свойствами корреляционной функции:
свойствами корреляционной функции:


 и
и
 .
. -
Случайные процессы
 и
и
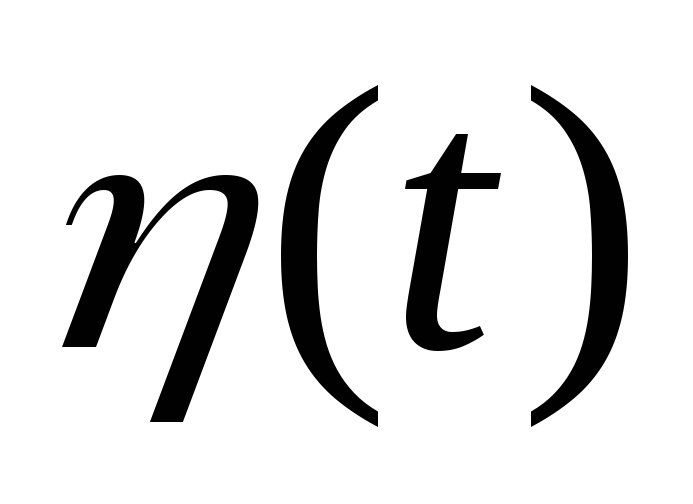 заданы своими математическими ожиданиями
заданы своими математическими ожиданиями
 ,
корреляционными
,
корреляционными
 и взаимными корреляционными функциями
и взаимными корреляционными функциями
 .
Определить математические ожидания и
корреляционные функции суммы и разности
этих процессов.
.
Определить математические ожидания и
корреляционные функции суммы и разности
этих процессов. -
Определить корреляционную функцию
 случайного процесса
случайного процесса
 ,
где
,
где
 - случайный процесс с нулевым математическим
ожиданием и корреляционной функцией
- случайный процесс с нулевым математическим
ожиданием и корреляционной функцией
 .
. -
Найти корреляционную функцию сигнала
 ,
где
,
где
 - стационарный случайный процесс с
нулевым математическим ожиданием и
корреляционной функцией
- стационарный случайный процесс с
нулевым математическим ожиданием и
корреляционной функцией
 ,
A
и ω
- постоянные величины, а φ
- случайная начальная фаза, равномерно
распределенная на интервале [-π;
π]
и не зависящая от
,
A
и ω
- постоянные величины, а φ
- случайная начальная фаза, равномерно
распределенная на интервале [-π;
π]
и не зависящая от
 .
. -
Определить корреляционную функцию комплексного случайного процесса
 , где
, где
 -
постоянная угловая частота,
-
постоянная угловая частота,
 взаимно не коррелированные случайные
величины с нулевыми математическими
ожиданиями
взаимно не коррелированные случайные
величины с нулевыми математическими
ожиданиями
 и дисперсиями
и дисперсиями
 .
. -
Определить математическое ожидание
 и корреляционную функцию
и корреляционную функцию
 периодически нестационарного случайного
процесса
периодически нестационарного случайного
процесса
 , где
, где
 - периодическая детерминированная
функция,
- периодическая детерминированная
функция,
 - стационарный случайный процесс с
математическим ожиданием
- стационарный случайный процесс с
математическим ожиданием
 и корреляционной функцией
и корреляционной функцией
 .
. -
Заданы два взаимно некоррелированных случайных процесса
 и
и
 с нулевыми математическими ожиданиями
и корреляционными функциями
с нулевыми математическими ожиданиями
и корреляционными функциями .
Доказать, что корреляционная функция
произведения этих процессов равна
произведению корреляционных функций
сомножителей:
.
Доказать, что корреляционная функция
произведения этих процессов равна
произведению корреляционных функций
сомножителей: .
.
-
Доказать, используя выражение для спектральной плотности, что не существует стационарного случайного процесса, корреляционная функция
 которого
была бы постоянна на временном интервале
которого
была бы постоянна на временном интервале
 и
равна нулю везде вне его.
и
равна нулю везде вне его. -
Случайный процесс
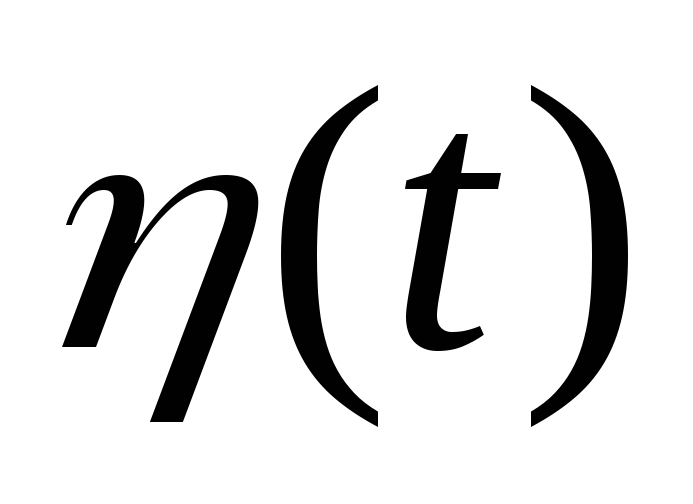 представляет собой последовательность
случайно чередующихся отрезков
элементарных сигналов
представляет собой последовательность
случайно чередующихся отрезков
элементарных сигналов
 и
и
 ,
т.е. имеет вид
,
т.е. имеет вид
 .
Здесь
.
Здесь
 и
и
 - стационарные и стационарно связанные
случайные процессы, не зависящие от
a(t),
а a(t)
- случайный
двоичный сигнал, который в любой момент
времени t
может
принимать одно из двух значений
- стационарные и стационарно связанные
случайные процессы, не зависящие от
a(t),
а a(t)
- случайный
двоичный сигнал, который в любой момент
времени t
может
принимать одно из двух значений
 или
или
 с одинаковыми вероятностями
с одинаковыми вероятностями
 ,
причем моменты скачков (перемен знака)
распределены по закону Пуассона, т.е.
вероятность обнаружения n
скачков на
интервале времени длительностью
,
причем моменты скачков (перемен знака)
распределены по закону Пуассона, т.е.
вероятность обнаружения n
скачков на
интервале времени длительностью
 определяется формулой
определяется формулой
 Вычислить корреляционную функцию
процесса
Вычислить корреляционную функцию
процесса
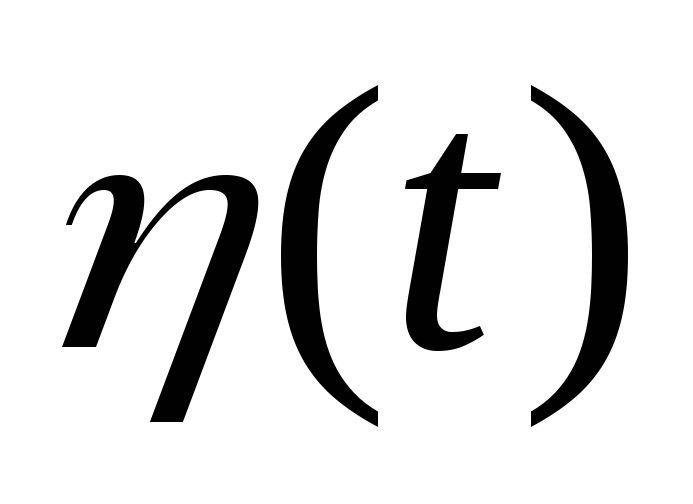 при условии, что математические ожидания
процессов
при условии, что математические ожидания
процессов
 и
и
 равны нулю, а их корреляционные и
взаимные корреляционные функции
известны:
равны нулю, а их корреляционные и
взаимные корреляционные функции
известны:
 ,
,
 и
и
 .
. -
Найти корреляционную функцию
 колебания
колебания
 ,
где
,
где
 - постоянные амплитуда и частота,
- постоянные амплитуда и частота,
 -
случайна начальная фаза, равномерно
распределенная на интервале
-
случайна начальная фаза, равномерно
распределенная на интервале
 ,
,
 - стационарные гауссовские случайные
функции, медленно меняющиеся по сравнению
с колебанием частоты
- стационарные гауссовские случайные
функции, медленно меняющиеся по сравнению
с колебанием частоты .
. -
Определить корреляционную функцию случайного процесса

 ,
где
,
где
 - стационарный случайный процесс с
нулевым математическим ожиданием и
корреляционной функцией
- стационарный случайный процесс с
нулевым математическим ожиданием и
корреляционной функцией
 .
. -
Вычислить ковариационную функцию двоичного сигнала
 ,
сформированного на основе простого
пуассоновского потока упорядоченных
временных точек
,
сформированного на основе простого
пуассоновского потока упорядоченных
временных точек
 следующим
образом:
следующим
образом:
 ,
если число точек в интервале
,
если число точек в интервале
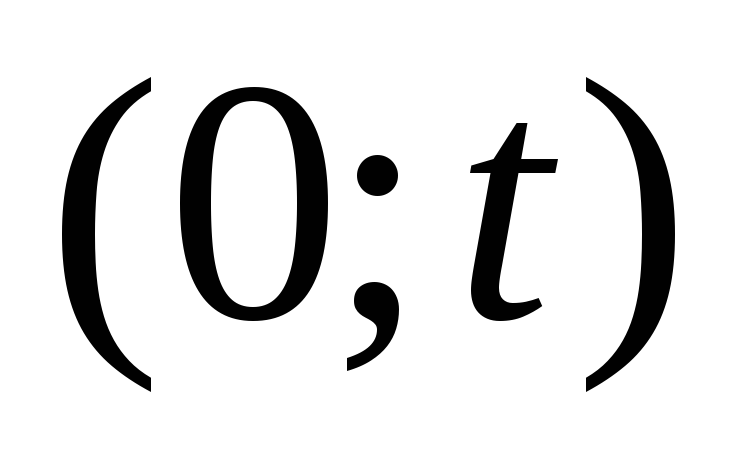 -
четное,
-
четное,
 ,
если число точек в интервале
,
если число точек в интервале
 -
нечетное.
-
нечетное. -
Исходя из того, что приращения простого пуассоновского потока
 на неперекрывающихся временных
интервалах независимы и распределены
по закону Пуассона с математическим
ожиданием
на неперекрывающихся временных
интервалах независимы и распределены
по закону Пуассона с математическим
ожиданием
 ,
найти математическое ожидание
произведения приращений на двух
интервалах, когда эти интервалы не
перекрываются и перекрываются.
,
найти математическое ожидание
произведения приращений на двух
интервалах, когда эти интервалы не
перекрываются и перекрываются. -
Получить выражение для ковариационной функции целочисленного пуассоновского процесса
 .
. -
Вычислить математическое ожидание и ковариационную функцию приращения простого пуассоновского процесса вида
 , где
, где
 -
заданная величина. Изобразить график
ковариационной функции и рассмотреть
предел
-
заданная величина. Изобразить график
ковариационной функции и рассмотреть
предел
 .
. -
Для простого пуассоновского процесса
 вычислить одномерную характеристическую
функцию.
вычислить одномерную характеристическую
функцию. -
Для простого пуассоновского процесса
 при
при
 и целых положительных
и целых положительных
 вычислить вероятность
вычислить вероятность
 .
. -
В законе Пуассона
 длительность временного интервала
длительность временного интервала
 является случайной величиной с плотностью
является случайной величиной с плотностью
 .
Найти вероятность появления ровно
.
Найти вероятность появления ровно
 событий.
событий.
Учебно-исследовательское задание
-
Флуктуации в электрических цепях. Теорема Найквиста и ее обобщения.
Литература
-
В.И.Тихонов. Статистическая радиотехника. М.: Радио и Связь, 1982.
-
В.Т.Горяинов, А.Г.Журавлев, В.И.Тихонов. Статистическая радиотехника. Примеры и задачи. М.: Сов.Радио, 1980.
Практическое занятие 15.
