§5. Система двох паралельних сил. Теорія пар на площині.

Система сил називається плоскою, якщо лінії дії сил лежать в одній площині. Система двох паралельних сил, що діють по різних прямих, завжди плоска.

5.1. Додавання двох паралельних сил. На відміну від двох збіжних сил, для додавання паралельних сил і , прикладених в точках А, В твердого тіла, не можна безпосередньо використати правило паралелограма. Тут можливі два випадки: 1) сили направлені в один бік; 2) сили направлені в протилежні боки.

1) Додавання двох сил, направлених в один бік. Розглянемо тверде тіло (мал. 1.23), на яке діють дві паралельні сили і . Прикладемо в точках А і В зрівноважену систему сил і , які направлені вздовж АВ(=-), і додамо їх до сил, за правилом паралелограма. Знайдені сили і перенесемо в точку О, в якій перетинаються лінії їх дії, і розкладемо на початкові складові. Після цього в точці О будуть діяти дві зрівноважені сили і , які відкидаємо, і дві паралельні сили , , що діють по одній прямій. Ці сили перенесемо в точку С і замінимо рівнодійною , величина якої дорівнює

К = F₁ + F₂ (1/10)

Сила буде рівнодійною сил і , прикладених в точках А і В. Для визначення положення точки С розглянемо трикутники ОАС, Оak, OCb, Omb. З умов подібності відповідних трикутників маємо

AC / OC = P₁ / F₁ ; BC / OC = P₂ / F₂,

або AC * F₁ = BC * F_{2 ,} бо P_{1 =} P₂

Враховуючи властивості пропорцій і рівності АВ = АС + СВ, R = F₁ + F₂, знаходимо BC/F₁ = AC/F₂ = AB/R. (1.11)

Співвідношення (1.11) мають назву правила важеля першого роду. Вони дозволяють розв’язувати обернену задачу про розклад сили на дві паралельні складові і .

Отже, рівнодійна двох співнаправлених паралельних сил має той самий напрям, що і складові, її величина визначається за формулою (1.10), а точка прикладення С — із співвідношення (1.11).

2) Додавання двох сил, направлених в протилежні боки. Розглянемо дві антипаралельні сили і , які прикладені в точках А і В твердого тіла, причому будемо вважати, що > . На прямій АВ з боку більшої сили виберемо точку С і прикладемо в ній зрівноважені сили і , паралельні силам і (мал. 1.24). при цьому величина цих сил і положення точки С визначаються рівностями R = F₁ – F₂; (1.12)

BC/F₂ = AC/F₁ = AB/R (1/13)

Додавши сили і , за формулами (1.10) і (1.11) визначимо силу , яка разом з силою утворює зрівноважену систему сил. В результаті цього задані сили будуть замінені рівнодійною , величина якої і положення визначаються рівностями (1.12), (1.13), причому остання називається правилом важеля другого роду.

Таким чином, система двох паралельних сил, направлених в протилежні боки, зводиться до рівнодійної, яка має напрямок більшої сили, її величина визначається формулою (1.12), а точка прикладання — із співвідношень (113).

3) Пара сил. Розглянемо випадок антипаралельних сил при F₁ = F₂ (мал. 1.25). Така система сил називається парою сил або парою. Оскільки сили і діють по різних прямих, то згідно аксіоми 1 пара сил не перебуває у рівновазі. В той же час пара сил не має рівнодійної. Якщо допустити протилежне, що пара (і ) має рівнодійну , то сила повинна цю пару зрівноважити. На основі теореми про три сили ,, повинні перетинатися в одній точці, що неможливо. Таким чином, пару сил не можна замінити або зрівноважити однією силою. Пара сил — самостійний об’єкт в статиці твердого тіла. Під час дії на тіло вона приводить до його обертання.

Площина, що визначається силами (і ), називається площиною дії пари, а відстань d між лініями дії сил — плечем пари.

5.2. Момент сили відносно точки. Нехай в точці А АТТ прикладена сила . Виберемо довільну точку О, яка разом з силою визначає площину α. З точки О проведемо перпендикуляр на лінію дії сили (пряму АВ). Довжина цього перпендикуляра h називається плечем сили відносно точки О (мал. 1.26).

Моментом сили відносно О (М₀()) називається число із знаком, що дорівнює добутку величини сили на плече

(1.14)

Момент сили відносно точки вважаємо додатнім, якщо сила обертає площину α навколо точки О проти годинникової стрілки (правило гвинта). Якщо обертання відбувається за годинниковою стрілкою, то момент — від’ємний.

Із означення момента сили відносно точки випливає:

1) Момент сили відносно точки дорівнює нулю тоді, і тільки тоді, коли лінія дії сили проходить через точку О (h=0).

2) Величина момента сили відносно точки дорівнює подвоєній площі трикутника, що визначається силою і точкою О.

Оскільки висота трикутника ОАВ не зміниться при переміщенні сили по прямій АВ, то обертальний ефект від момента сили буде залежати від її величини, напрямку і плеча. Вимірюється момент сили відносно точки в ньютоно-метрах (Н*м).

За допомогою поняття момента сили відносно точки зручніше визначати точку С прикладання системи двох паралельних сил. Враховуючи (1.14), ліві частини рівностей (1.11) і (1.13) можна подати у вигляді

(1.15)

Отже, точка прикладання рівнодійної системи двох паралельних сил визначається з умови перетворення в нуль суми моментів цих сил відносно шуканої точки. Рівність (1.15) являє собою окремий випадок відомої теореми Варіньона: якщо система двох паралельних сил має рівнодійну, то її момент відносно будь-якої точки дорівнює сумі моментів складових сил відносно цієї точки.

Точне доведення теореми буде приведене при розгляді просторової системи сил.

5.3. Момент пари. Розглянемо пари сил і (=), які діють в площині α (мал. 1.27). оскільки пара сил, прикладена до твердого тіла, викликає обертальний ефект, то для оцінки його величини необхідно ввести кількісну характеристику пари. Виберемо в площини довільну точку О і обчислимо відносно неї суму моментів сил пари.

(1.16)

Остання рівність показує, що сума моментів сил пари відносно довільної точки площини α є величина постійна і не залежить від вибору точки. Цю величину приймемо за кількісну характеристику пари сил і назвемо моментом пари .

Моментом пари будемо називати число зі знаком, яке дорівнює добутку однієї із сил пари на плече. Знак момента пари вибирається за правилом гвинта (рух площини дії пари проти годинникової стрілки). На мал. 1.27 пара і має додатковий момент. Момент пари вимірюється в тих же одиницях, що і момент сили відносно точки (Н*м).

5.4. Еквівалентність пар. Доведемо теорему, яка разом з наслідками, що випливають з неї, визначає основні властивості пар на площині.

Теорема: Дві пари, що діють в одній площині і мають однакові моменти, еквівалентні.

Доведення. Для доведення теореми необхідно показати, що одну пару можна перетворити в другу при допомозі додавання і розкладання сил.

Розглянемо дві пари сил і , і , причому сили і непаралельні. (мал. 1.28). Знаходимо точку перетину відповідних ліній дії сил пар. В точці А перенесемо силу , а в точку В — силу . Розкладемо ці сили по напрямках АВ і ВD.

(1.17)

Оскільки сили і зрівноважені, то їх можна відкинути.

Таким чином, пара (,) перетворена в еквівалентну їй пару (,). Момент цієї пари, згідно теореми Варіньона, дорівнює

(1.18)

Пари () і () мають однакові моменти . Тому Р₁=Р. Теорема доведена. У випадку паралельності сил і , для доведення теореми слід використовувати правила додавання і розкладання паралельних сил. Із доведеної теореми дістаємо такі властивості сил на площині:

1. не змінюючи вплив на тіло, пару сил можна довільно переміщати в площині її дії;

2. в заданій парі можна довільно змінювати величину сил або плече, залишаючи незмінним її момент, при цьому дія пари на тіло не змінюється.

Звідси випливає, що дія пари на тверде тіло характеризується лише її моментом. Тому, особливо в техніці, пару сил зображують круговою стрілкою, яка вказує напрямок повороту, не зображаючи самі сили. На мал. 1.29 показано, що на тіло діє сила і пара з моментом m.

5.5. Додавання пар, розміщених в одній площині. Умови рівноваги системи пар.

Теорема: система пар, розміщених в одній площині еквівалентна одній парі, що діє в тій же площині, момент якої дорівнює алгебраїчній сумі моментів складових пар.

Доведення. Допустимо, для спрощення доведення, що на тверде тіло в одній площині діє три пари з моментами m₁, m₂, m₃ (мал. 1.30). На підставі попередньої теореми замінимо задані пари трьома парами з спільним плечем АВ=d і тими ж самими моментами

З останніх рівностей сили , , визначаються однозначно. Додавши окремо, прикладені в точках А і В, матимемо в точці В силу , а в точці А — силу , які за величиною дорівнюватимуть

Це означає, що систему трьох пар ми замінили однією парою (,) з моментом . Такий же результат ми дістанемо при довільному числі пар. Теорема доведена.

Таким чином, розв’язок першої задачі статистики для системи пар на площині може бути сформульований так: довільна система пар на площині може бути зведена до однієї пари, момент якої дорівнює алгебраїчній сумі моментів складових пар

(1.19)

Із доведеної теореми випливає, що для рівноваги системи пар на площині необхідно і достатньо, щоб алгебраїчна сума моментів цих пар дорівнювала нулю

(1.20)

Співвідношення (1.20) виражає собою розв’язок другої задачі статики для системи пар на площині. За механічним змістом умова (1.20) забезпечує відсутність обертання твердого тіла в площині дії пар.

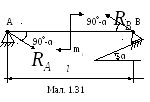Приклад 2. На горизонтальну балку АВ довжиною l діє пара сил з моментом m₁. Визначити реакції опори, якщо ліва опора А являє собою нерухомий шарнір, а права опора В — рухомий циліндричний каток (мал.1.31).

Розв'язування. Опора В шарнірно рухома, тому реакція направлена перпендикулярно до площини руху катка. Напрямок реакції невизначений. Оскільки зовнішню пару сил можна зрівноважити тільки парою, то реакції і повинні утворювати пару сил . Запишемо умову рівноваги системи пар:

З даної рівності знаходимо