Неперервність функції.

Означення. Функція називається неперервною в точці , якщо виконуються наступні умови:

1. функція визначена в точці, тобто ;

2. існує границя функції в точці, тобто ;

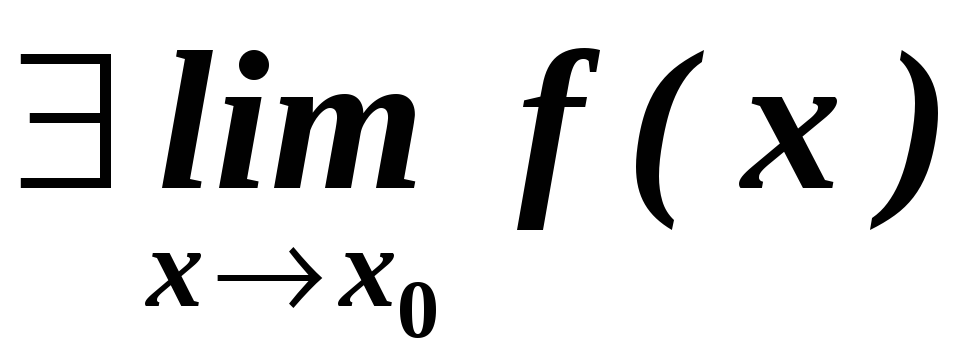3. границя співпадає зі значенням функції, тобто .

Наведемо декілька еквівалентних означень.

Означення. Функція називається неперервною в точці , якщо при знак границі і знак функції можна переставити місцями.

Означення. Функція називається неперервною в точці , якщо нескінченно малим приростам аргументу відповідають нескінченно малі прирости функції, тобто .

Означення. Функція називається неперервною в точці , якщо існують односторонні границі, вони співпадають між собою і дорівнюють значенню функції в точці, тобто

.

Базуючись на означенні та властивостях збіжних функцій, неважко впевнитись у справедливості наступного твердження.

Теорема. Якщо функції і неперервні в точці , то неперервними в цій точці будуть: алгебраїчна сума , добуток та частка при умові .

Доведення.

Означення. Функція називається неперервною на множині , якщо вона неперервна в кожній точці цієї множини.

Наведені вище означення та властивості дозволяють стверджувати, що на своїх областях визначення неперервні складені, обернені і, взагалі, будь-які елементарні функції.

Класифікація точок розриву.

Означення. Функція називається розривною в точці , якщо порушується хоча б одна із трьох умов ( 1), 2) або 3) )неперервності в цій точці.

В залежності від того, яка із умов порушується, а яка виконується, здійснюється класифікація точок розриву.

Означення. Якщо виконується умова 2): і порушуються умова 3) або 1) і 3), то називають точкою усувного розриву («прокол»).

Відзначимо, що у цьому випадку можна доозначити або переозначити функцію в точці по неперервності.

Приклад. Розглянемо функції:

на проміжку ;

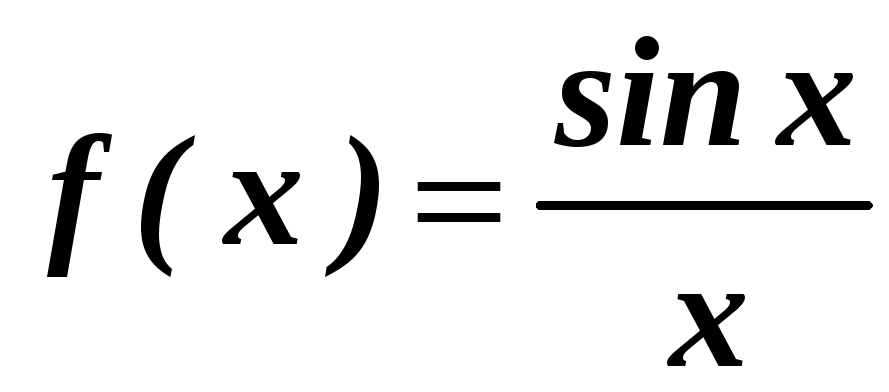в околі точки .

Розв’язування.

Розглянемо тепер випадок, коли порушується умова 2) існування границі функції в точці.

Означення. Якщо в точці існують, але не співпадають односторонні границі: , то називають точкою розриву першого роду («стрибок»).

Приклад. Розглянемо функцію 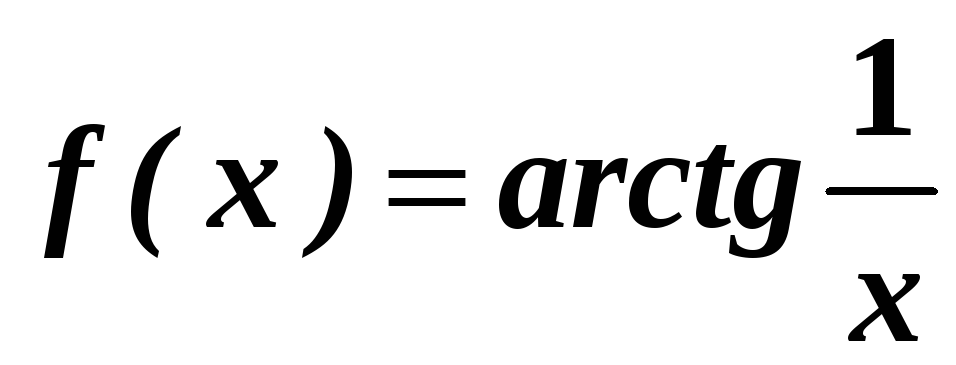в околі точки .

Розв’язування.

Означення. Якщо в точці не існує хоча б одна із односторонніх границь: , то називають точкою розриву другого роду.

Приклад. Розглянемо функцію 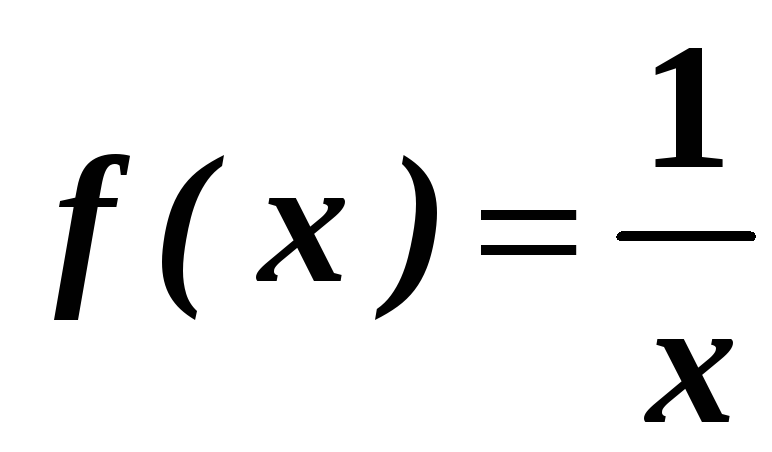в околі точки .

Розв’язування.

Приклад. Дано функцію

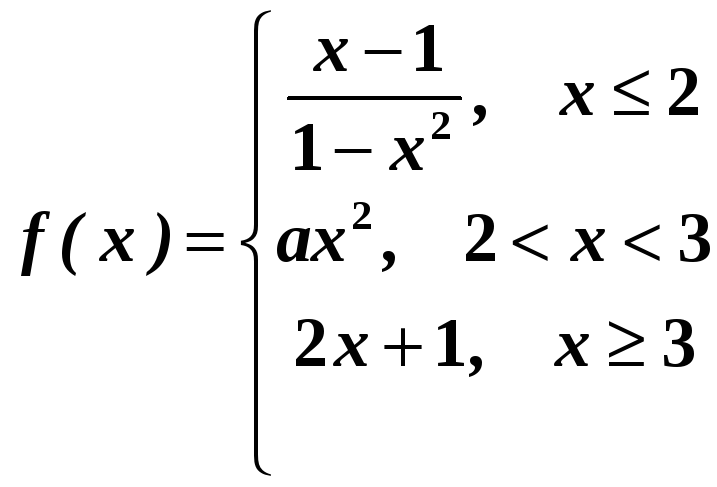
Знайти значення параметра , при якому функція неперервна в точці . Дослідити отриману функцію на неперервність.

Розв’язування.

Властивості функцій, неперервних на замкненому проміжку.

Теорема (про корінь фнкції). Якщо функція неперервна на сегменті і на його кінцях набуває значень різного знаку , тоді на інтервалі існує корінь функції, тобто .

Графічна ілюстрація:

Теорема (Вейерштрасса). Якщо функція неперервна на сегменті , то вона досягає на цьому сегменті своїх найбільшого та найменшого значень, тобто

.

Графічна ілюстрація:

Теорема (про проміжне значення). Якщо функція неперервна на сегменті , то вона набуває на цьому сегменті будь-якого значення між своїми найменшим та найбільшім , тобто

.

Графічна ілюстрація: