Розділ ііі. Вступ до аналізу

Тема 11: Функції. Основні поняття. Послідовності. Границя послідовності. Властивості границі. Функції. Основні поняття.

Означення. Якщо кожному значенню змінної за деяким певним законом (або правилом) ставиться у відповідність єдине значення , то кажуть , що задана (визначена) однозначна функція . При цьому, множину називають областю визначення функції, - множиною її значень, - аргументом (незалежною змінною), - функцією від (залежною змінною).

Зауваження. Всюди надалі розглядаються лише однозначні функції, тому слово «однозначні» опускатимемо. Слід відмітити, що функції та - різні, оскільки вони визначені на різних проміжках. Цей приклад показує, що функція – це «триєдине» нерозривне поняття (область визначення, закон відповідності та множина зміни значень).

Серед способів задання функцій найбільш поширеними є табличний, графічний та аналітичний. Якщо функція задається аналітично (формулою) і не вказується множина зміни аргументу, то областю визначення функції вважають область допустимих значень аргументу (тобто, всі значення аргументу, при яких аналітичний вираз має сенс).

Означення. Графіком функції називається множина точок площини із координатами , де , .

Часто графіком є деяка крива (наприклад, для функції - парабола), але взагалі кажучи, це може бути досить екзотична множина.

Над функціями можна виконувати звичайні арифметичні операції (алгебраїчна сума, множення, ділення), враховуючи їх допустимість на спільній області визначення. Розглянемо деякі специфічні операції.

Означення. Нехай функція визначена , а функція визначена , причому . Тоді на визначена складена функція , або суперпозиція фунцій і . При цьому називають внутрішньою, а - зовнішньою фунціями.

Наприклад, складена функція є суперпозицією внутрішньої та зовнішньої функцій.

Означення. Нехай функція визначена , причому різним значенням аргумента відповідають різні значення функції (тобто, ). Тоді можна визначити обернену функцію із областю визначення та множиною значень .

Наприклад, для лінійної функції оберненою буде також лінійна функція 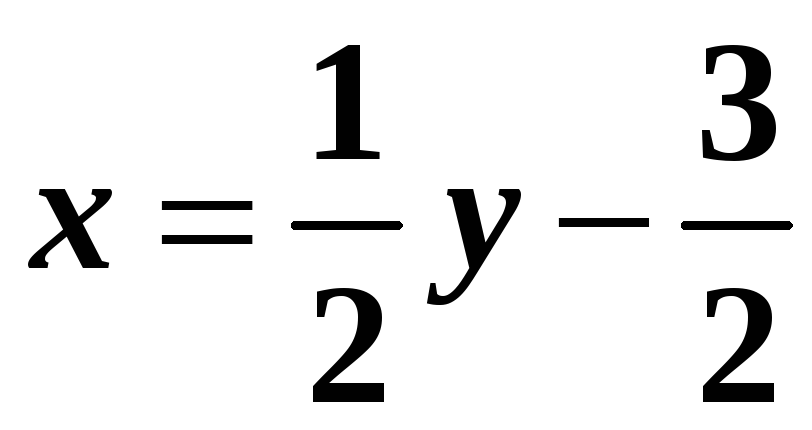. Для функції оберненою буде функція . Але для функції не можна визначити обернену функцію, оскільки у неї різним значенням аргумента можуть відповідати однакові значення функції ( наприклад,). У таких випадках для визначення оберненої функції із області визначення виділяють проміжки, на яких виконується умова взаємно однозначної відповідності між аргументом та функцією: оберненою для функції буде функція .

Означення. Функція , що визначена на деякій множині , називається обмеженою на цій множині, якщо існує деяке число таке, що .

Графік обмеженої функції знаходиться в полосі між прямими та .

Означення. Функція , що визначена на деякій множині , називається необмеженою на цій множині, якщо для будь-якого числа існує таке, що .

Означення. Функція , що визначена на деякій множині , зростає (неспадає) на цій множині, якщо виконується умова ( ).

Означення. Функція , що визначена на деякій множині , спадає (незростає) на цій множині, якщо виконується умова ( ).

Означення. Зростаючі, спадаючі, неспадаючі, незростаючі функції називаються монотонними, причому, зростаючі та спадаючі називають строго монотонними.

Означення. Функція , що визначена , називається парною (непарною), якщо виконується умова: ( ).

Графік парної функції симетричний відносно осі ординат, а непарної – відносно початку координат.

Якщо ж умови парності (непарності) не виконуються, або область визначення несимметрична відносно початку координат, то кажуть, що функція загального вигляду.

Означення. Функція , що визначена на деякій множині , називається періодичною, якщо існує число , таке, що виконується рівність . При цьому найменше із таких чисел називається періодом.

Означення. Основними елементарними функціями називають: степеневу ; показникову ; логарифмічну ; тригонометричні ; обернені тригонометричні .

Означення. Елементарними називають функції, які отримують за допомогою скінченної кількості арифметичних операцій та суперпозицій над основними елементарними функціями.

Наведемо декілька прикладів неелементарних функцій. По-перше, це функції, які задаються при різних значеннях аргумента різними елементарними функціями: 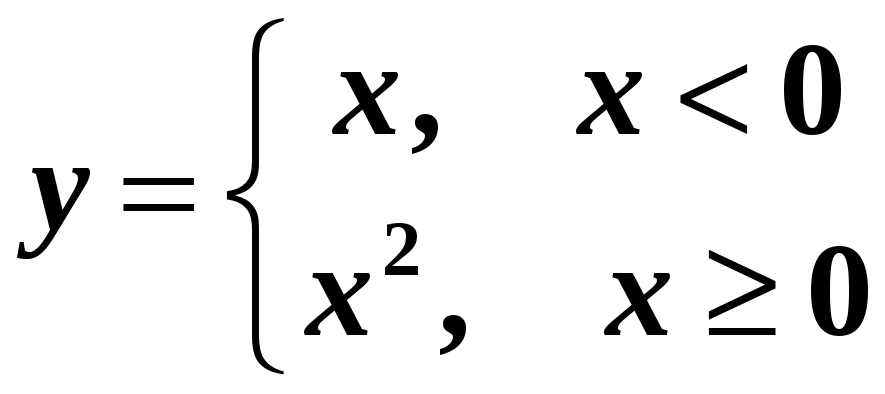. 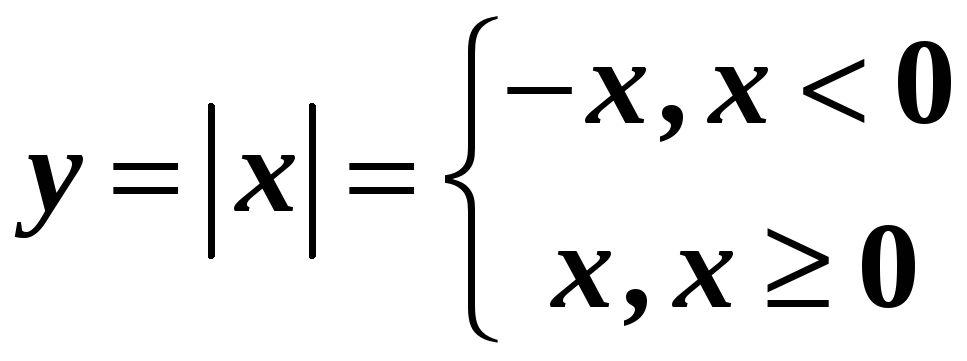, - ціла частина числа тощо.