Послідовності.

Означення. Числовою послідовністю називається функція натурального аргументу і позначається , де , тобто область визначення – множина натуральних чисел , а множина значень – члени послідовності: . - називають її загальним членом, за допомогою якого задається послідовність.

Приклади.

1) : ;

2) : ;

3) : ;

4) : ;

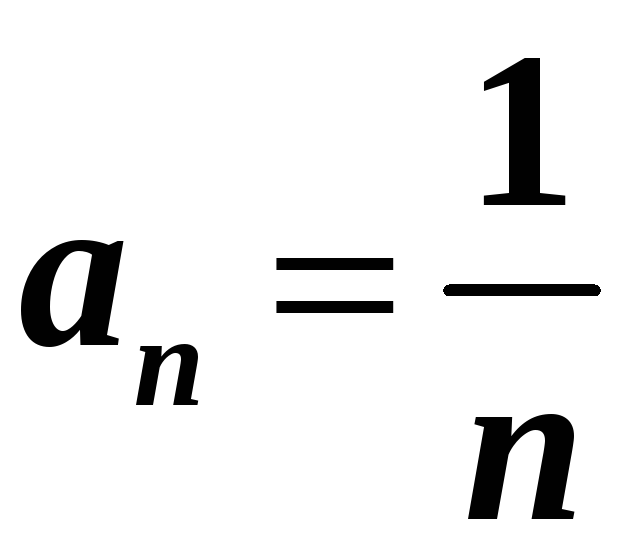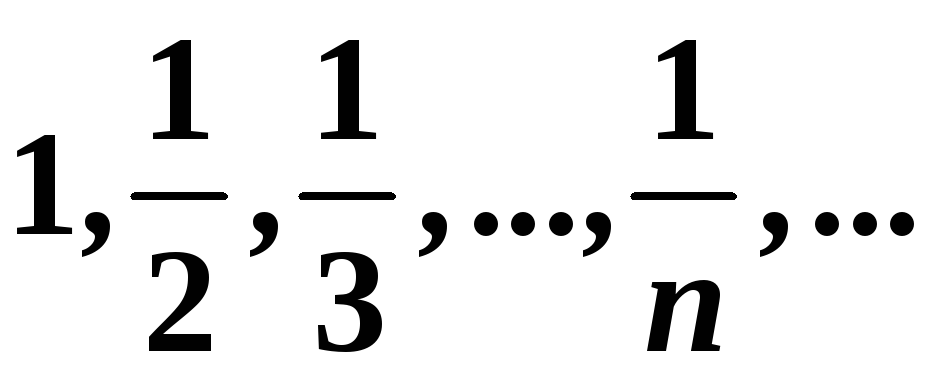5) : .

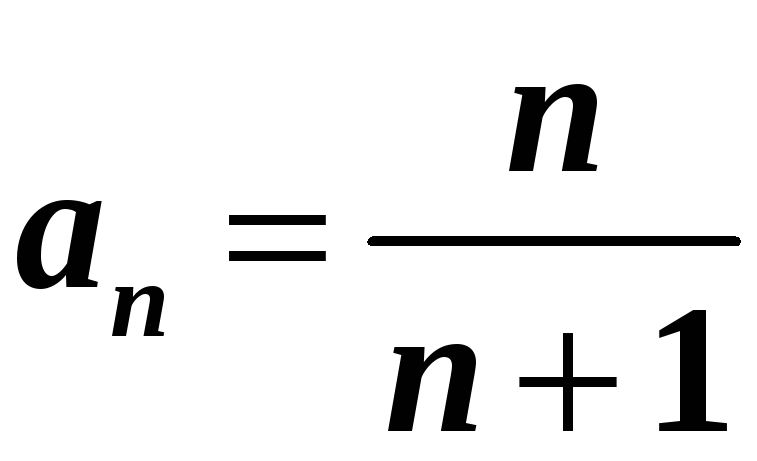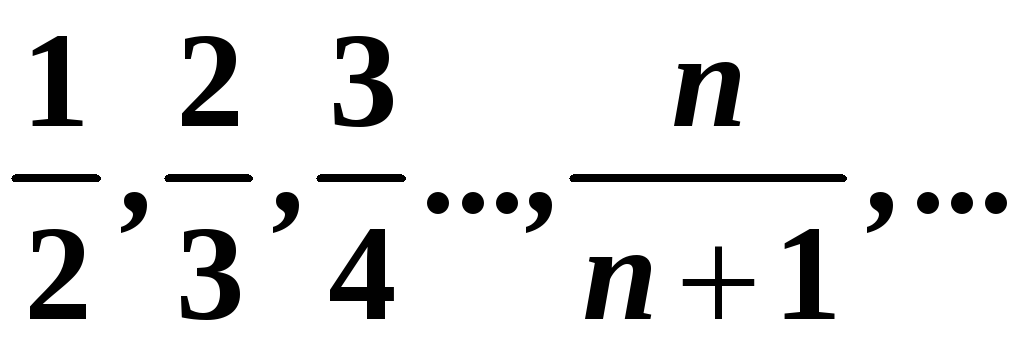Графічне зображення цих послідовностей на числовій осі:

дозволяє зробити висновок, що деякі послідовності мають так звану «точку згущення».

Задамо довільне додатне число (як завгодно мале). «Епсілон-околом» точки називається проміжок (інтервал) .

Означення (геометричне). Точка називається границею послідовності , якщо будь-який -окіл точки містить усі члени послідовності, починаючи з деякого номера .

Еквівалентні означення.

Означення (геометричне). Точка називається границею послідовності , якщо поза будь-яким -окілом точки міститься лише фіксована кількість членів послідовності.

Означення. Число називається границею послідовності , якщо

.

Якщо послідовність має границю , то її називають збіжною і позначають: або . У супротивному випадку послідовність називають розбіжною.

Доведемо за означенням, що послідовності 1), 4), 5) збіжні:

Доведемо за означенням, що послідовність 3) розбіжна:

Властивості границі.

Теорема 1 (єдиність). Якщо послідовність має границю, то ця границя єдина.

Доведення.

Теорема 2 (обмеженість). Якщо послідовність має границю, то ця послідовність є обмеженою.

Доведення.

Зауваження. Взагалі кажучи, не будь-яка обмежена послідовність є збіжною (див. приклад обмеженої послідовності 3) ).

Теорема 3 (збереження знаку). Якщо послідовність має границю , то всі члени послідовності, починаючи з деякого мають знак границі .

Доведення.

Приклад послідовності 1) показує справедливість наступного твердження.

Теорема 4 (границя сталої). Границя сталої послідовності дорівнює самій цій сталій.

ТЕМА 12: Нескінченно малі (НМ) та нескінченно великі (НВ) послідовності, їх властивості. Порівняння НМ та НВ. Арифметичні теореми для збіжних послідовностей. Теореми порівняння. Теорема Вейерштрасса, чудова границя.

Нескінченно малі (НМ) та нескінченно великі (НВ) послідовності, їх властивості. Порівняння НМ та НВ.

Означення. Послідовність називається нескінченно малою (НМ), якщо її границя дорівнює нулю, тобто

.

Властивості нм

Теорема 1 (зв’язок НМ і збіжної). Для того, щоб послідовність мала границю , необхідно і достатньо (НІД), щоб послідовність була НМ.

Доведення.

Теорема 2. Алгебраїчна сума двох НМ є НМ.

Доведення.

Теорема 3. Добуток обмеженої послідовності на НМ є НМ.

Доведення.

Наслідок. Добуток двох НМ є НМ.

Теореми та наслідок легко розповсюджується на фіксовану кількість доданків (співмножників).

Означення. Означення. Послідовність називається нескінченно великою (НВ), якщо для довільного (як завгодно великого) додатного числа всі члени послідовності, починаючи з деякого, по модулю більші цього числа, тобто

.

Звернемо увагу на те, що НВ не має границі ( - позначення НВ). Окрім того, будь-яка НВ є необмеженою, але обернене твердження невірне (наведіть приклад).

Аналогічно попереднім властивостям НМ, базуючись на зв’язку НМ та НВ, доводяться наступні властивості НВ.

Теорема 4 (зв’язок НМ і НВ). Для того, щоб послідовність була НВ НІД, щоб послідовність 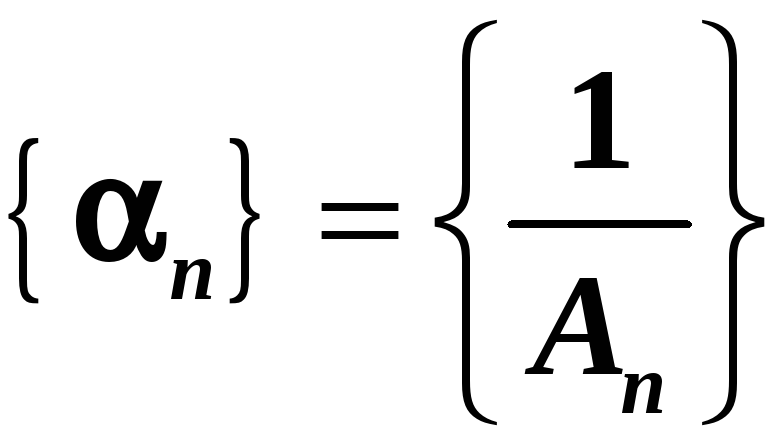була НМ.

Доведення.

Теорема 5. Сума фіксованої кількості НВ одного знака є НВ.

Теорема 6. Добуток обмеженої на НВ є НВ.

Наслідок. Добуток фіксованої кількості НВ є НВ.

Якщо позначити НМ: , а НВ: , то їх властивості можна записати у наступному вигляді:

Зауваження. Наступні послідовності можуть бути НМ, НВ, збіжними або розбіжними (так звані «невизначеності»): .

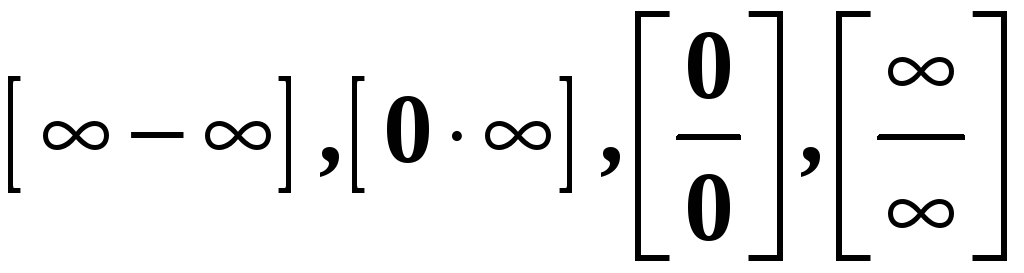При знаходженні границь корисно вміти порівнювати НМ та НВ. Нехай послідовності , - НМ, а , - НВ. Розглядаються послідовності їх відношень: 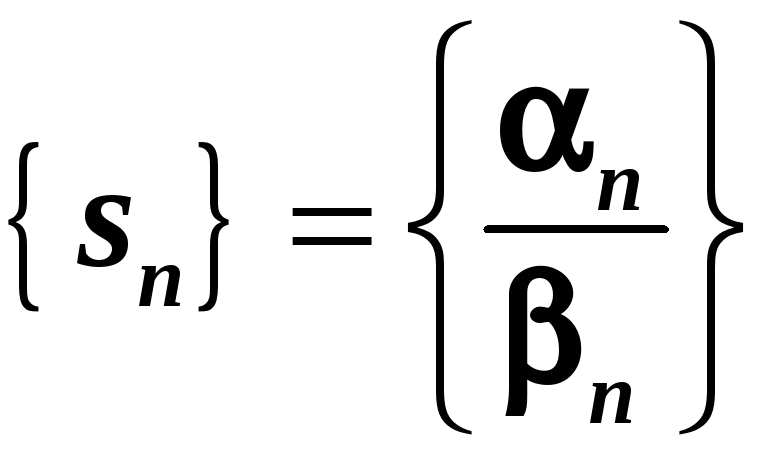для НМ і .

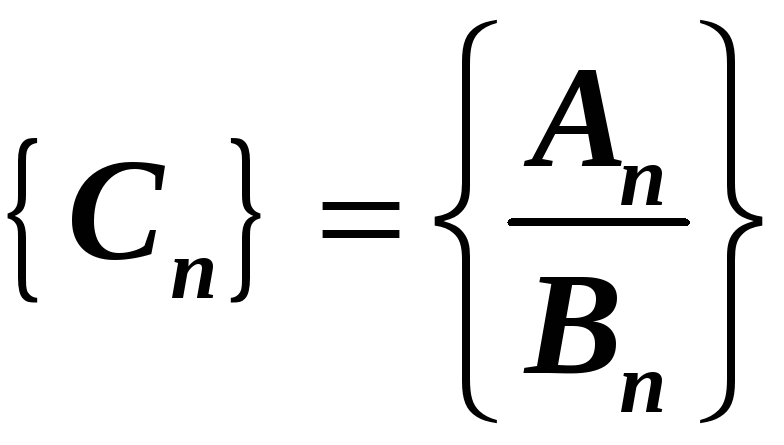Якщо , то кажуть, що - НМ більш високого порядку, ніж .

Якщо , то кажуть, що - НМ більш високого порядку, ніж .

Якщо , то кажуть, що і - НМ одного порядку, зокрема, якщо , то і - еквівалентні НМ.

Якщо , то кажуть, що - НВ більш високого порядку, ніж .

Якщо , то кажуть, що - НВ більш високого порядку, ніж .

Якщо , то кажуть, що і - НВ одного порядку, зокрема, якщо , то і - еквівалентні НВ.

Наприклад, при аргументі, що прямує до нескінченності, многочлен є НВ, еквівалентною старшому одночлену. Дійсно: