§3. Обернена матриця

Повернемось до операції ділення матриць (яку визначимо як добуток на обернену матрицю).

Нехай 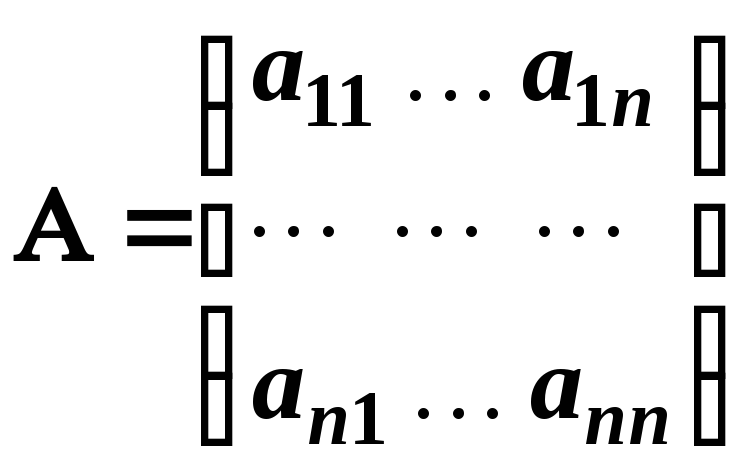– ­­квадратна матриця порядку .

Означення. Матриця називається оберненою до матриці , якщо

- одинична матриця.

Зауваження. Очевидно, що – квадратна матриця того ж порядку, що і .

Означення. Квадратна матриця називається невиродженою, якщо її визначник . У противному разі матриця називається виродженою.

Справедлива така

Теорема. Для існування оберненої матриці до квадратної матриці необхідно і достатньо, щоб її визначник (тобто матриця повинна бути невиродженою).

Схема знаходження оберненої матриці

1. Знаходимо визначник матриці . Якщо 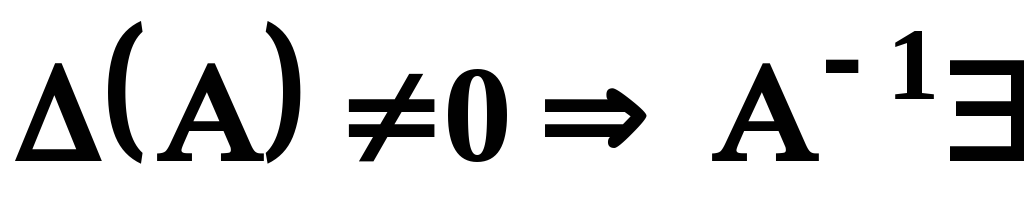, якщо ж 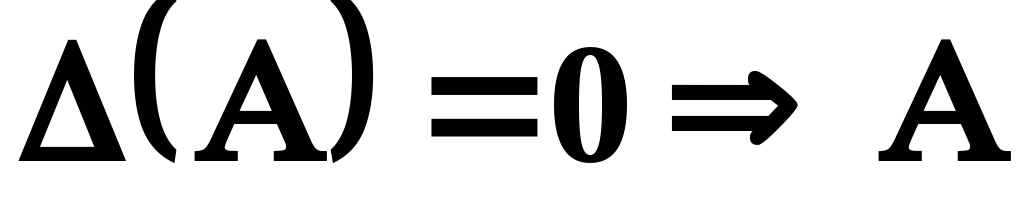- вироджена, і 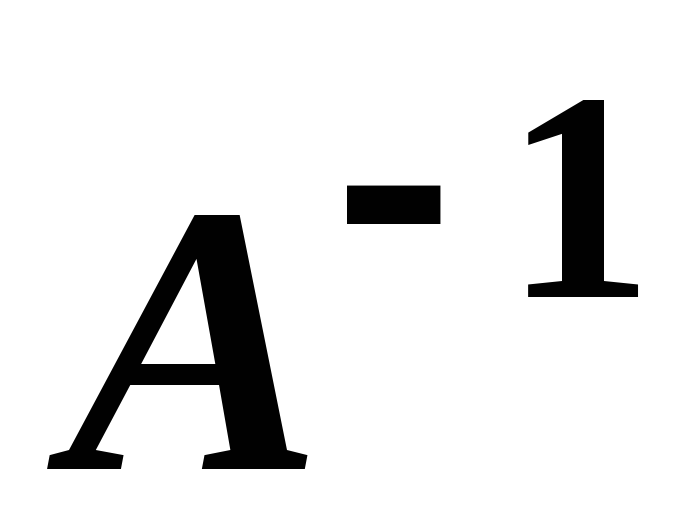не .

2. Знаходимо – алгебраїчні доповнення усіх елементів визначника.

3. Записуємо обернену матрицю:

.

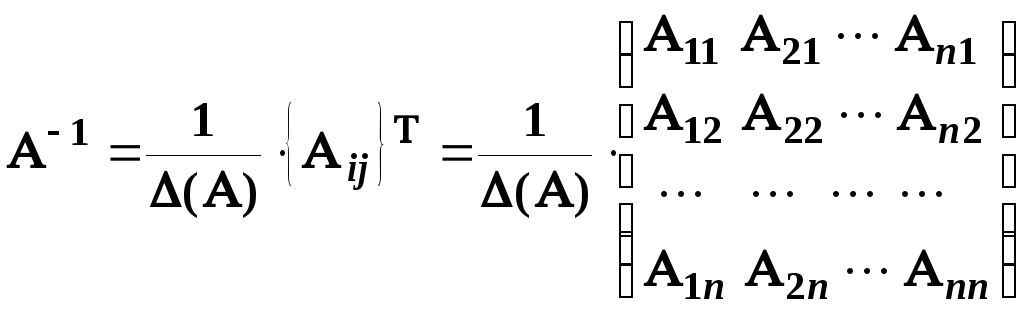4. Якщо потрібно, виконуємо перевірку:

(або ).

Наприклад, знайти обернену для матриці

.

Розв’язування.

1. . .

2. Знаходимо алгебраїчні доповнення :

; ;

; ;

; ;

; ;

.

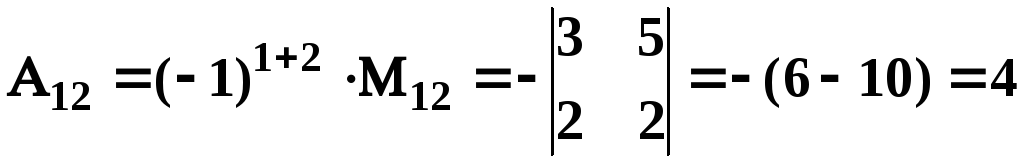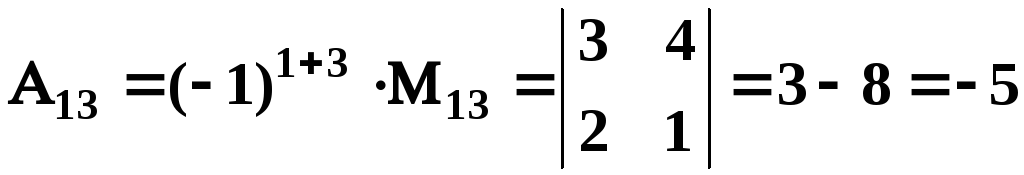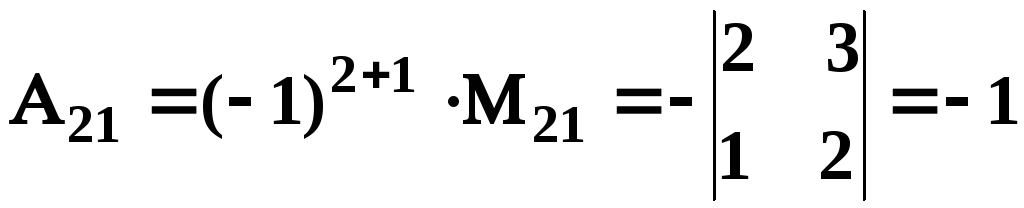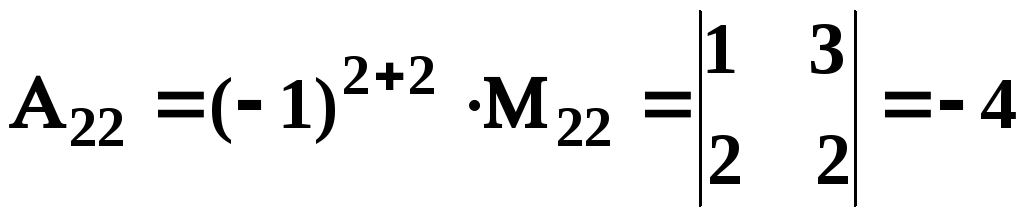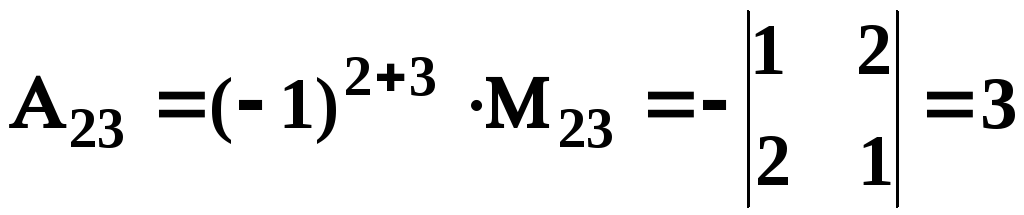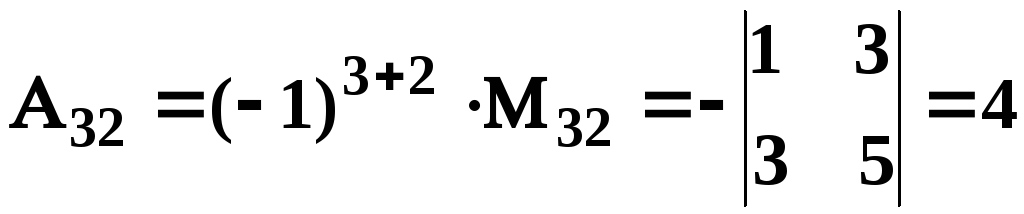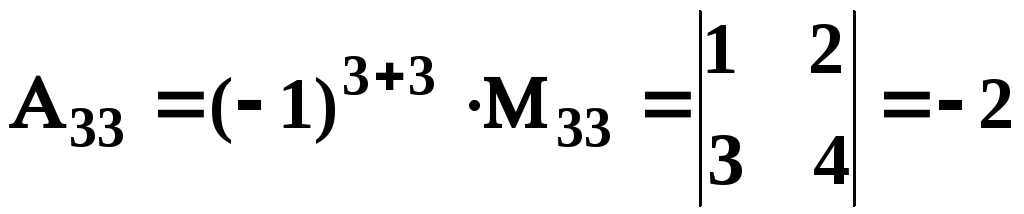3. Записуємо обернену матрицю:

.

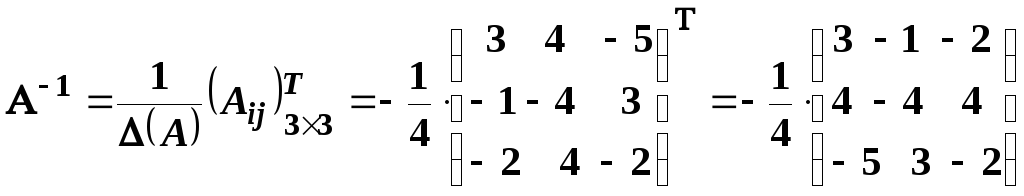4. Перевірка:

Завдання для самостійного розв’язування

3.1. Для даної матриці знайти обернену матрицю , якщо існує.

а); б) ; в) ; г) .

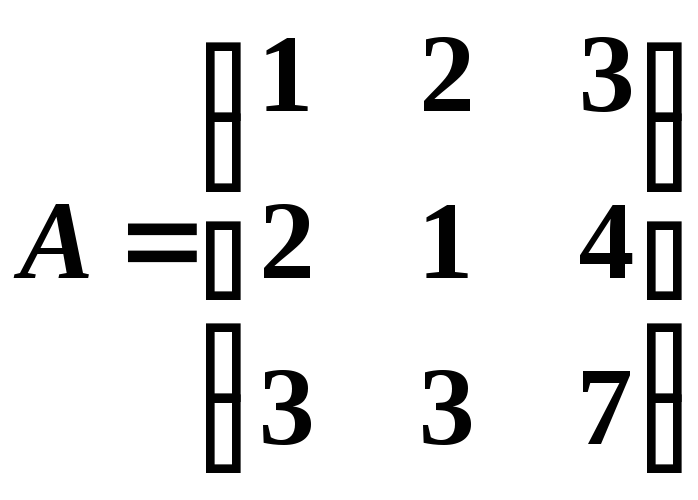Відповіді:

3.1. а); б) ;

в) ; г) Не існує.

§4. Розв’язування систем лінійних рівнянь з невідомими за допомогою оберненої матриці та за правилом Крамера

Розглянемо систему лінійних алгебраїчних рівнянь (СЛАР) з невідомими:

(*).

Означення . Розв’язком СЛАР (*) називається упорядкована множина дійсних чисел , яка при підстановці у систему замість невідомих перетворює її в систему тотожностей.

Матричний метод

Позначимо:

, , .

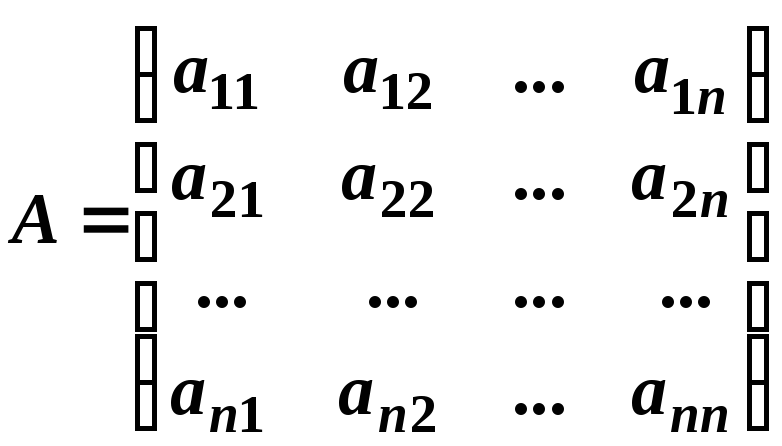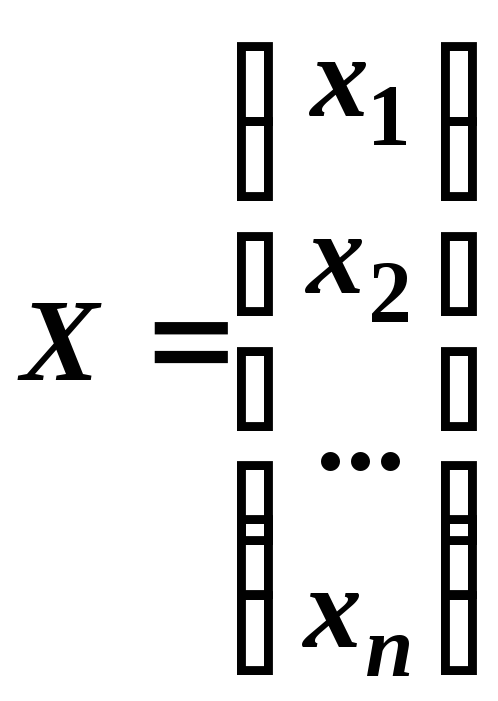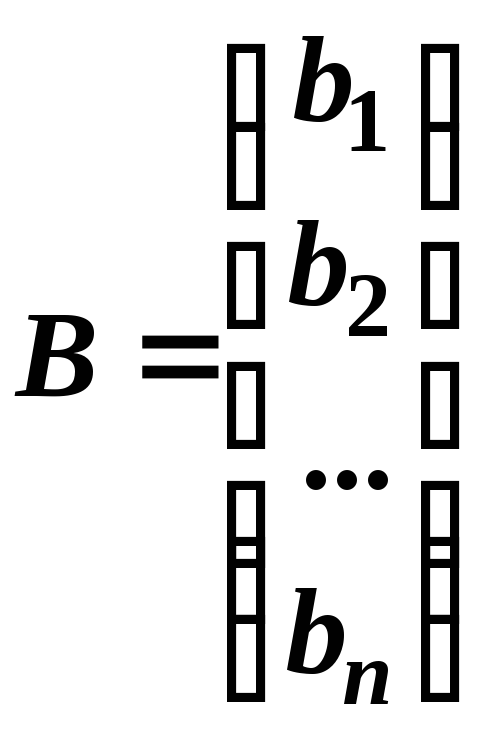Тут: – матриця коефіцієнтів при невідомих (основна матриця системи);

– матриця-стовпець невідомих;

– матриця-стовпець вільних членів (правих частин).

Тоді СЛАР (*) можна записати у вигляді матричного рівняння:

.

Якщо , то існує . Домножимо обидві частини матричного рівняння зліва на . Одержимо:

,

,

.

Отже, справедлива така

Теорема. Якщо визначник основної матриці СЛАР (*) відмінний від нуля , то система має єдиний розв’язок, який знаходиться як добуток оберненої до матриці на матрицю–стовпець вільних членів .

Приклад. Розв’язати за допомогою оберненої матриці СЛАР:

.

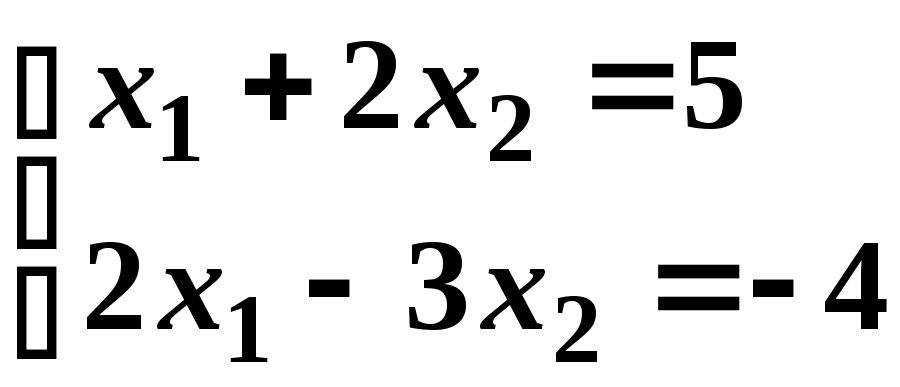Розв’язування.

1. Позначимо:

– матриця коефіцієнтів при невідомих;

– матриця-стовпець невідомих;

– матриця-стовпець вільних членів.

2. Запишемо систему у вигляді матричного рівняння .

3. Обчислимо : система має єдиний розв’язок. Оскільки , то існує обернена матриця .

Знайдемо її:

Отже, .

Таким чином,

.

Відповідь: , .

Метод Крамера

Означення . Основним визначником СЛАР (*) називається визначник матриці коефіцієнтів при невідомих .

Справедлива така

Теорема (правило Крамера). Якщо основний визначник СЛАР (*) , то система має єдиний розв’язок, який знаходиться за формулами:

; ; …; ,

де визначники отримуємо із заміною -го стовпця коефіцієнтів при невідомій на стовпець вільних членів.

Приклад. Розв’язати систему рівнянь за правилом Крамера.

.

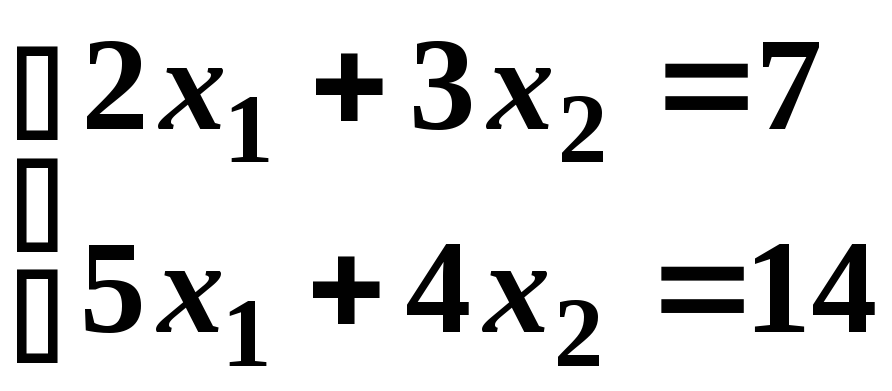Розв’язування.

, .

Оскільки , то система має єдиний розв’язок, що знаходиться за правилом Крамера:

, .

; .

Перевірка: .

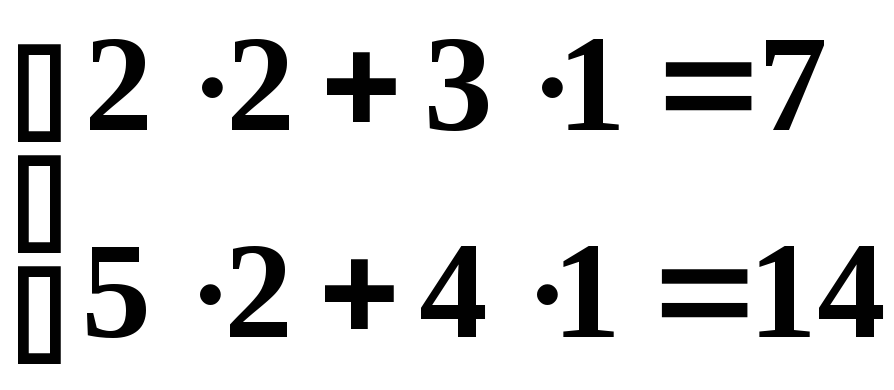Відповідь: .