
- •Розділ I. Лінійна алгебра
- •§1. Матриці. Різновиди матриць. Дії над матрицями
- •Дії над матрицями
- •Завдання для самостійного розв’язування
- •§ 2. Визначники, їх властивості.
- •Властивості визначників
- •Завдання для самостійного розв’язування
- •§3. Обернена матриця
- •Завдання для самостійного розв’язування
- •§4. Розв’язування систем лінійних рівнянь з невідомими за допомогою оберненої матриці та за правилом Крамера
- •Матричний метод
- •Метод Крамера
- •Завдання для самостійного розв’язування.
- •§5. Ранг матриці і його обчислення
- •Методом елементарних перетворень
- •Завдання для самостійного розв’язування
- •§6. Дослідження і розв’язування систем лінійних рівнянь з невідомими
- •Розв’язування систем m лінійних рівнянь з n невідомими методом Жордана-Гаусса
- •Завдання для самостійного розв’язування
- •Розділ іі. Аналітична геометрія
- •§1. Метод координат
- •§2. Елементи векторної алгебри
- •Основні означення
- •§3. Дії над векторами
- •Умова колінеарності
- •Скалярний добуток
- •Завдання для самостійного розв’язування
- •§4. Найпростіші задачі аналітичної геометрії
- •Завдання для самостійного розв’язування
- •§5. Рівняння лінії
- •§6. Пряма лінія
- •Дослідження загального рівняння прямої
- •Рівняння прямої, що проходить через дану точку паралельно даному вектору (канонічне рівняння прямої)
- •Рівняння прямої, що проходить через дві задані точки
- •Рівняння прямої у відрізках на осях
- •Відстань від точки до прямої
- •Кутовий коефіцієнт прямої. Рівняння прямої з кутовим коефіцієнтом
- •Взаємне розташування двох прямих. Умова паралельності та перпендикулярності прямих
- •Завдання для самостійного розв’язування
- •§7. Перетворення системи координат
- •Паралельне перенесення
- •2. Поворот координатних осей
- •§8. Криві іі порядку
- •Характеристична властивість точок еліпса
- •Характеристична властивість точок м(х; у) гіперболи
- •Рівнобічна гіпербола
- •Характеристична властивість точок параболи (геометричне означення параболи).
- •Завдання для самостійного розв’язування
- •Відповіді:
Розділ I. Лінійна алгебра
§1. Матриці. Різновиди матриць. Дії над матрицями
Означення.
Матрицею розміру
![]() (читається: „ем на ен”) називається
таблиця упорядкованих чисел (або
будь-яких інших об’єктів), розташованих
в
(читається: „ем на ен”) називається
таблиця упорядкованих чисел (або
будь-яких інших об’єктів), розташованих
в
![]() рядках
та в
рядках
та в
![]() стовпцях.
стовпцях.
Матриці
позначають великими літерами
![]() та круглими дужками.
та круглими дужками.
Наприклад,
числова матриця розміру
![]() має вигляд:
має вигляд:
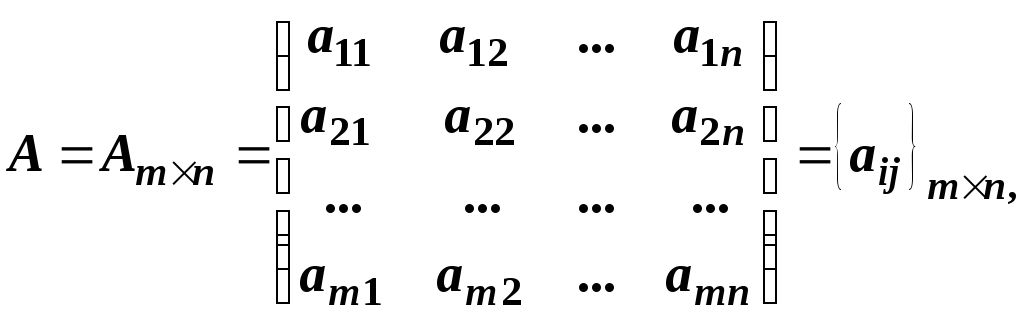 ,
,
де
![]() – номер
рядка,
а
– номер
рядка,
а
![]() – номер
стовпця,
на перетині яких знаходиться число
– номер
стовпця,
на перетині яких знаходиться число
![]() – елемент
матриці.
– елемент
матриці.
Матриця
розміру
![]() називається матрицею-стовпцем
(або вектор-стовпцем), а матриця розміру
називається матрицею-стовпцем
(або вектор-стовпцем), а матриця розміру
![]() називається матрицею-рядком
(або вектором-рядком).
називається матрицею-рядком
(або вектором-рядком).
Матриця,
всі елементи якої дорівнюють нулю,
називається нуль-матрицею
і позначається
![]() .
.
Наприклад,
 – матриця
розміру
– матриця
розміру
![]() ;
;
![]() – нуль-матриця
розміру
– нуль-матриця
розміру
![]() ;
;
-
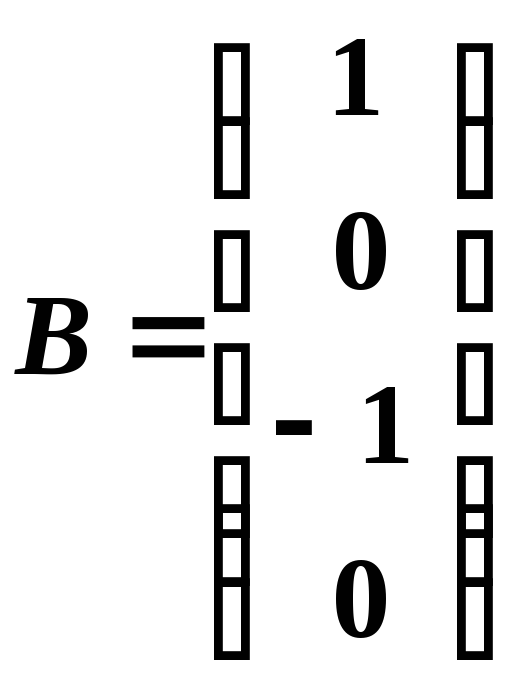
– матриця-стовпець розміру
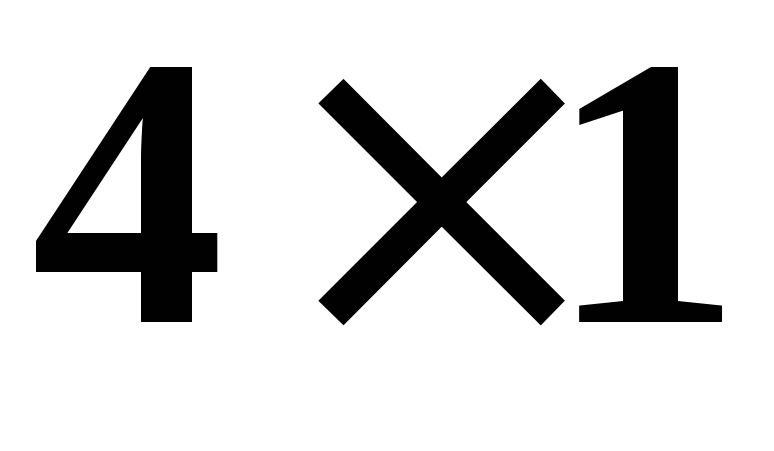 (або вектор
(або векторстовпець розмірності 4)
![]() – матриця-рядок
розміру
– матриця-рядок
розміру
![]() (або трьохвимірний вектор-рядок).
(або трьохвимірний вектор-рядок).
Матрицю
![]() ,
у якої
,
у якої
![]() (тобто, кількість рядків співпадає із
кількістю стовпців) називають квадратною
матрицею порядку
(тобто, кількість рядків співпадає із
кількістю стовпців) називають квадратною
матрицею порядку
![]() :
:
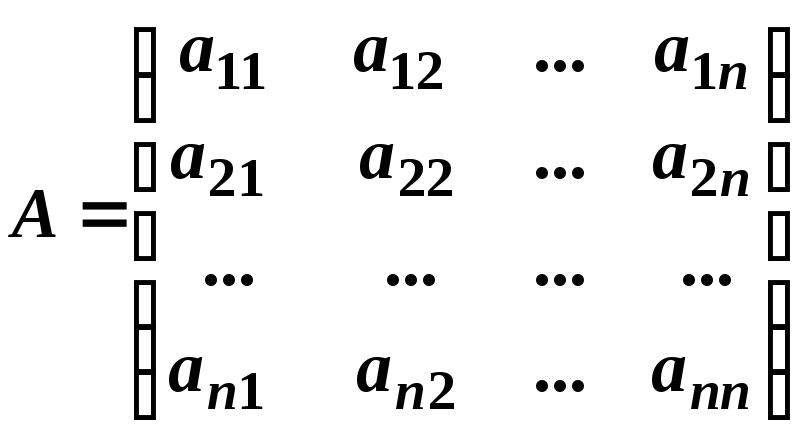
Множина
елементів
![]() квадратної матриці
квадратної матриці
![]() порядку
порядку
![]() називається головною
діагоналлю,
а множину елементів
називається головною
діагоналлю,
а множину елементів
![]() називають побічною
діагоналлю
(або неголовною, допоміжною).
називають побічною
діагоналлю
(або неголовною, допоміжною).
Квадратна матриця, у якої всі елементи, розташовані під головною діагоналлю (над головною діагоналлю), дорівнюють нулю, називається верхньою (нижньою) трикутною.
Квадратна матриця, у якої всі позадіагональні елементи дорівнюють нулю, називається діагональною і часто позначається
![]() .
.
Діагональна
матриця, у якої всі діагональні елементи
дорівнюють одиниці, називається одиничною
і позначається
![]() .
.
Наприклад, матриці:
![]() – квадратна
порядку 2;
– квадратна
порядку 2;
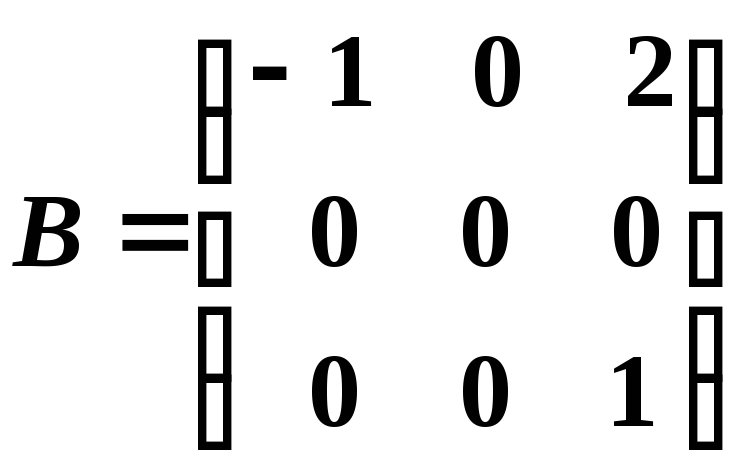 – верхня
трикутна;
– верхня
трикутна;
![]() – нижня
трикутна;
– нижня
трикутна;
![]() – діагональна
2-го порядку,
– діагональна
2-го порядку,
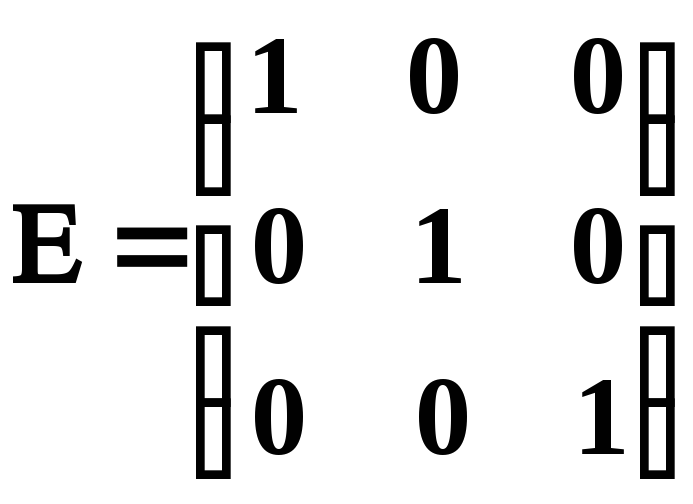 – одинична
3-го порядку.
– одинична
3-го порядку.
Дії над матрицями
1. Порівняння. Матриці однакових розмірів рівні між собою, якщо співпадають їх відповідні елементи.
Наприклад:
![]() ,
,
![]() ,
,
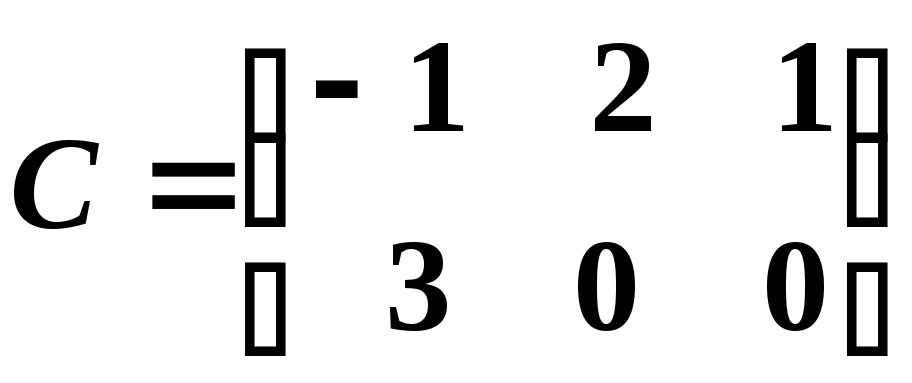 .
.
![]() ,
оскільки
,
оскільки
![]() ;
;
![]() ,
оскільки матриці різних розмірів.
,
оскільки матриці різних розмірів.
2.
Транспонування. Транспонованою
до матриці
![]() називають матрицю
називають матрицю
![]() (або
(або
![]() ),
рядки якої дорівнюють відповідним
стовпцям матриці
),
рядки якої дорівнюють відповідним
стовпцям матриці
![]() .
.
Наприклад,
для
 .
.
Очевидно,
що
![]() .
.
3. Множення на число. Для того, щоб помножити матрицю на число (або число на матрицю), потрібно кожен елемент матриці помножити на це число.
Наприклад,

4. Додавання (віднімання). Сумою (різницею) двох матриць однакових розмірів буде матриця, елементи якої знаходяться додаванням (відніманням) відповідних елементів матриць-доданків.
Наприклад, два підприємства випускають три види продукції, причому, на початок та на кінець року випуски задаються відповідно матрицями
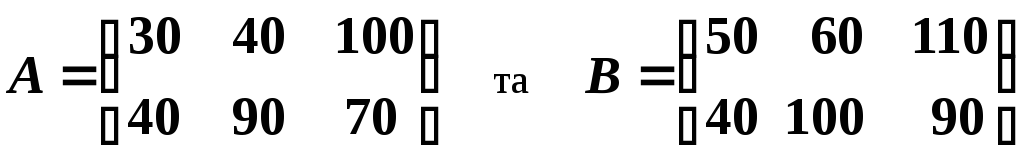 ,
,
де
![]() –випуски на початок та на кінець року
–випуски на початок та на кінець року
![]() -им
підприємством
-им
підприємством
![]() -го
виду продукції. Знайти для кожного
підприємства і кожного виду продукції:
а)
середньорічний випуск; б)
приріст продукції за рік.
-го
виду продукції. Знайти для кожного
підприємства і кожного виду продукції:
а)
середньорічний випуск; б)
приріст продукції за рік.
Розв’язування. а) середньорічний випуск дорівнює:
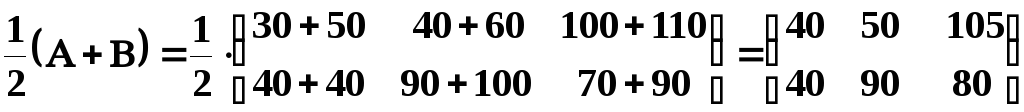
б) приріст продукції за рік дорівнює:
 .
.
5.
Множення матриць.
Добутком двох матриць
![]() називається матриця
називається матриця
![]() ,
кожен елемент якої
,
кожен елемент якої
![]() дорівнює сумі добутків елементів
дорівнює сумі добутків елементів
![]() –го
рядка матриці
–го
рядка матриці
![]() на відповідні елементи
на відповідні елементи
![]() –го
стовпця матриці
–го
стовпця матриці
![]() („рядки 1–ої множаться на стовпчики
2–ої”):
(„рядки 1–ої множаться на стовпчики
2–ої”):
![]() .
.
Зауваження.
Із означення випливає, що добуток
![]() існує, якщо матриці „узгоджені”, тобто
число стовпців матриці
існує, якщо матриці „узгоджені”, тобто
число стовпців матриці
![]() співпадає з числом рядків матриці
співпадає з числом рядків матриці
![]() .
.
На
практиці, для знаходження
![]() -го
рядка добутку двох матриць потрібно
-го
рядка добутку двох матриць потрібно
![]() -ий
рядок першої матриці послідовно,
„накладанням” помножити на всі стовпці
другої матриці.
-ий
рядок першої матриці послідовно,
„накладанням” помножити на всі стовпці
другої матриці.
Наприклад, знайти добуток матриць
![]() і
і
 .
.
Розв’язування.
![]() -
„узгоджені”, значить
-
„узгоджені”, значить
![]() існує.
існує.
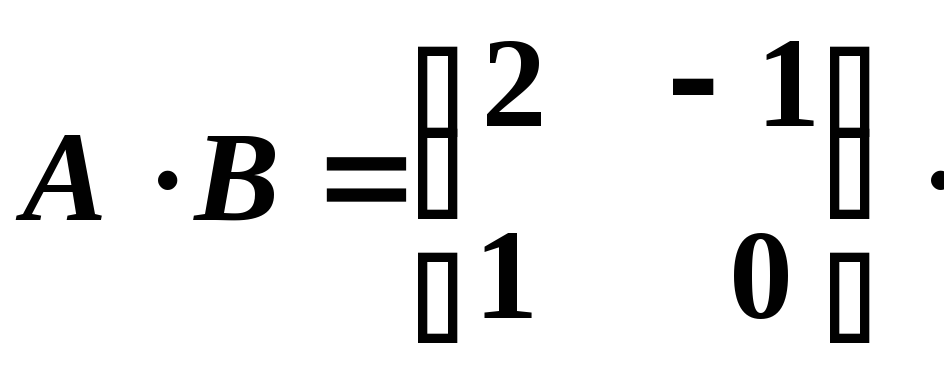
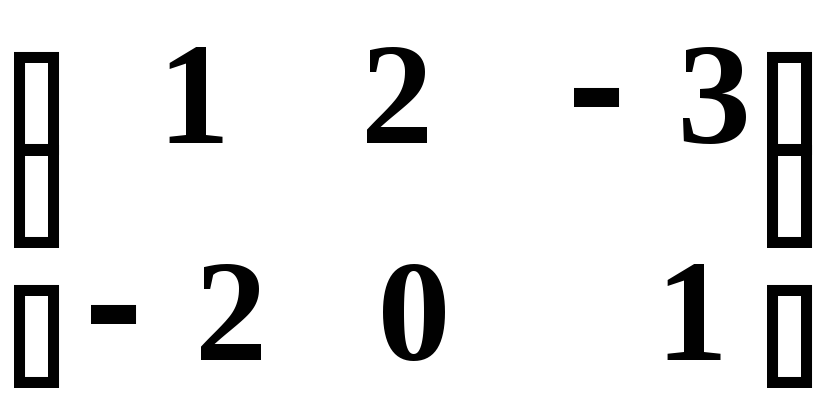 =
=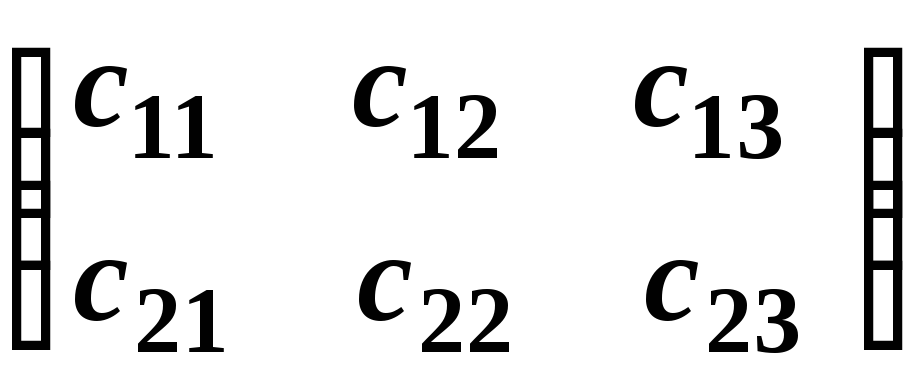 .
.
![]()
![]()
![]()
Знаходження елементів 1–го рядка добутку:
С11: 2 -1 С12: 2 -1 С13: 2 -1
1 -2 2 0 -3 1 _
2·1+(-1)·(-2)=4 2·2+(-1)·0=4 2·(-3)+(-1)·1=-7
Знаходження елементів 2–го рядка добутку:
С21: 1 0 С22: 1 0 С23: 1 0
1 -2 2 0 -3 1 _
1·1+0·(-2)=1 1·2+0·0=2 1·(-3)+0·1=-3
Отже:
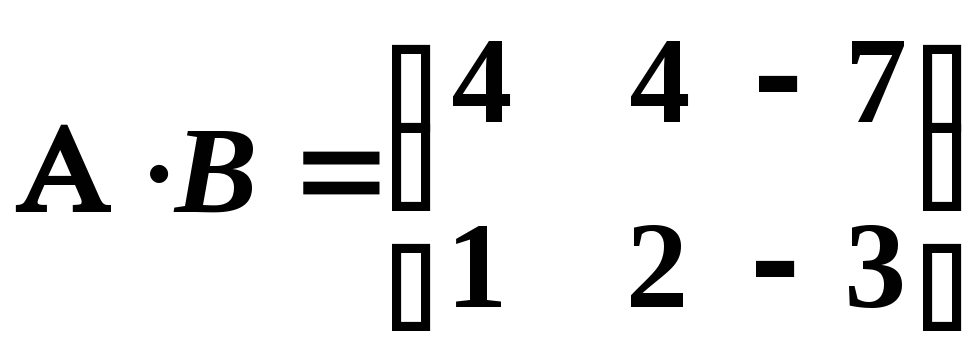 .
.
Зазначимо,
що добуток
![]() – не існує (оскільки
– не існує (оскільки
![]() і
і
![]() „неузгоджені”).
„неузгоджені”).
Зауваження.
Добуток
матриць, взагалі кажучи, не має властивості
комутативності, тобто
![]() (навіть, якщо існують обидва добутки і
їх розміри співпадають), але є матриці,
для яких
(навіть, якщо існують обидва добутки і
їх розміри співпадають), але є матриці,
для яких
![]() (комутативні).
(комутативні).
Наприклад,
для
квадратних
одного порядку матриць
![]() і
і
![]() ,
,
![]() .
.
Дійсно:
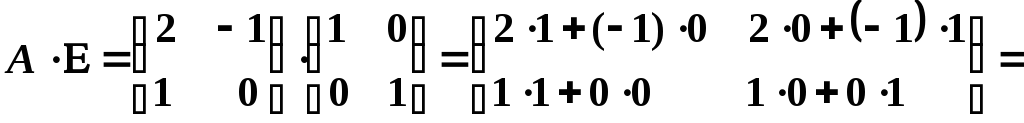
![]()
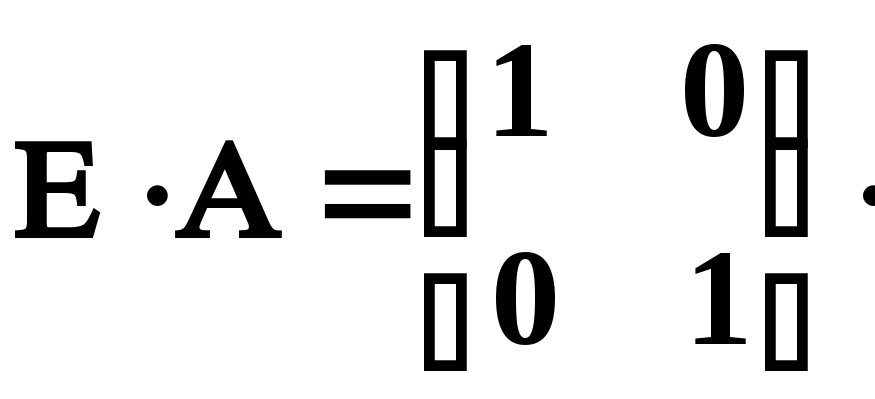
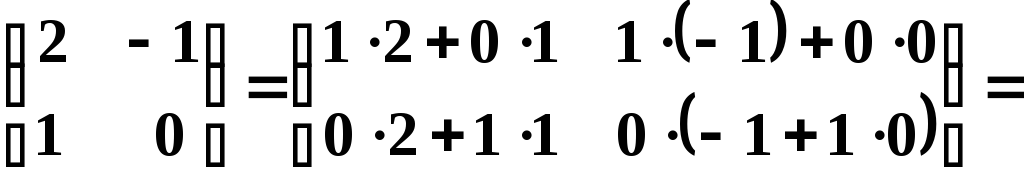
![]()
Приклад
показує, що одинична матриця
![]() відіграє таку ж саму роль у матричному
численні, що і
відіграє таку ж саму роль у матричному
численні, що і
![]() при множенні чисел.
при множенні чисел.
6.
Ділення матриць.
Для матриць ділення
![]() визначають як добуток
визначають як добуток
![]() ,
де
,
де
![]() – матриця, обернена до матриці
– матриця, обернена до матриці
![]() ,
визначення і знаходження якої розглянемо
далі.
,
визначення і знаходження якої розглянемо
далі.
Зауваження. Введені вище операції над матрицями підкоряються асоціативним, дистрибутивним та комутативним законам, аналогічним числовим, із урахуванням специфіки дій над матрицями.
