
- •1. Основные определения. Технология моделирования
- •2. Методология моделирования
- •3. Анализ моделируемой системы и постановка задач
- •4.Второй этап моделирования. Формализация. Решение Задачи. Выбор метода моделирования
- •5. Корреляционный анализ
- •6.Третий этап моделирования. Разработка имитационных моделей.
- •7.Генерация равномерно-распределенных случайных чисел. Оценка их качества на тестах (по книге).
- •Тест частот
- •8.Планирование имитационных экспериментов. Концепция «черного ящика» Планирование экспериментов
- •9.План дфэ (дробных факторных экспериментов).
- •10. Рцкп (ротатабельный центральный композиционный план).
- •12.Тактическое планирование имитационных эксперементов
- •14.Основные свойства системы Arena.
- •15. Кластерный анализ. Евклидово расстояние. Ближайший сосед. Наиболее удаленный сосед. По среднему значению. Расстояние Хемминга.
- •1. Фр, фп, мпф, Равномерный экспоненциальный закон.
- •2. Метод моментов. Равномерный закон.
- •Метод моментов для равномерного закона
- •3. Метод моментов. Нормальный закон.
- •4. Метод моментов. Экспоненциальный закон.
- •5. Метод моментов. Гиперэкспоненциальный закон.
- •Решим полученное квадратное уравнение.
- •6. Метод моментов. Специальный эрланговский закон.
- •7. Метод обратной функции. Достоинства и недостатки.
- •Достоинства и недостатки аналитического метода генерации случайных чисел
- •8. Табличный метод генерации случайных чисел. Достоинства и недостатки.
- •9. План пфэ (полного факторного эксперимента).
- •10. План оцкп (ортогональный центральный композиционный план).
- •12. Применение дисперсионного анализа для оценки качества уравнений регрессии. Оценка значимости коэффициентов полинома.
- •13. Метод оптимизации по системе ур-й в частных производных.
- •14. Геометрический метод для 2 факторов.
- •15. Метод Ньютона.
- •1. Временные динамические ряды. Основные понятия. Проверка гипотез о существовании тенденций. Временные ряды
- •2. Сглаживание и прогнозирование методом скользящих средних. В чем смысл введения взвешиваний.
- •Сглаживание
- •Метод скользящих средних
- •Взвешенные скользящие средние
- •3. Сглаживание и прогнозирование экспоненциальных средних
- •4. Прогнозирование на нейронных сетях Прогнозирование на нейронных сетях
- •5. Группировка. Общие понятия. Постановка задачи и технология проведения кластерного анализа.
4.Второй этап моделирования. Формализация. Решение Задачи. Выбор метода моделирования
На данном этапе решаются следующие задачи:
Задача 1. Производится переход от функциональных зависимостей результативных показателей эффективности от влияющих на них факторов (1.1) к математическим зависимостям.
Задача 2. Количественные характеристики функционирования элементов ОМ, заданные на предыдущем этапе последовательностями случайных чисел, представляются стандартными статистическими законами.
Задача 3. Выбирается метод исследования.
1. В лучшем случае при переходе от функциональных зависимостей к математическим нам известен закон, то есть вид математической зависимости результативных показателей эффективности от факторов и тогда задача сводится только к вычислению коэффициентов этой известной математической зависимости, но чаще всего вид математической зависимости не известен. В этом случае рекомендуется использовать для её представления степенные полиномы. При увеличении степени полинома можно через экспериментальные точки провести математическую зависимость с любой заданной достоверностью. На рис. 11.1 показано представление экспериментальной зависимости, заданной координатами пяти точек, линейным полиномом и полиномом четвёртой степени. В последнем случае линия зависимости y=f(x) проходит точно через все экспериментальные точки. Линейное представление y=f(x) характеризуется некоторой ошибкой.
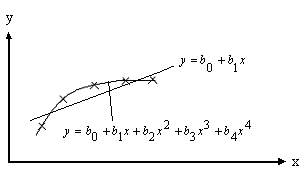
Для однофакторной зависимости используется полином к-ой степени:
.![]()
Для двух факторов можно использовать полином второй степени:
![]() .
Отметим, что на данном этапе мы выбираем
только вид аппроксимирующей зависимости
– степенной полином. А степень полинома
определяется по величине стандартной
ошибки представления экспериментальных
данных математической зависимостью.
.
Отметим, что на данном этапе мы выбираем
только вид аппроксимирующей зависимости
– степенной полином. А степень полинома
определяется по величине стандартной
ошибки представления экспериментальных
данных математической зависимостью.
5. Корреляционный анализ
Корреляция – это соотношение (взаимозависимость) случайных величин между собой. В качестве количественной меры оценки взаимосвязи между случайными величинами используется коэффициент линейной корреляции, вычисляемый для случайных величин х и у по n экспериментальным данным по следующей формуле.
![]() В формуле оценка
математического ожидания произведения
переменных х
и у
вычисляется
по формуле:
В формуле оценка
математического ожидания произведения
переменных х
и у
вычисляется
по формуле:
Е![]() сли
коэффициент линейной корреляции близок
к 1,
то корреляционная связь между переменными
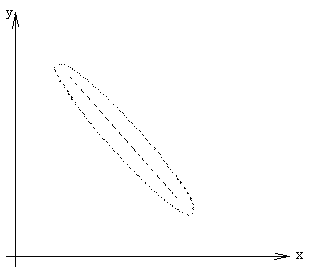
положительная, близкая к линейной Если
коэффициент линейной корреляции близок
к -1,
то корреляционная связь между переменными
отрицательная, близкая к линейной
(рис.16.2). Если коэффициент линейной
корреляции близок к
0, то между
переменными имеется слабая корреляционная
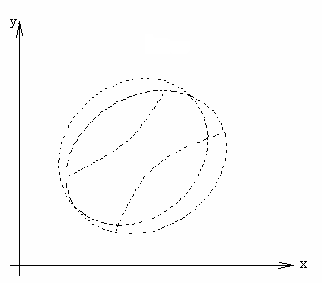
связь (рис.16.3). Для независимых переменных
коэффициент линейной корреляции равен
нулю.
сли
коэффициент линейной корреляции близок
к 1,
то корреляционная связь между переменными
положительная, близкая к линейной Если
коэффициент линейной корреляции близок
к -1,
то корреляционная связь между переменными
отрицательная, близкая к линейной
(рис.16.2). Если коэффициент линейной
корреляции близок к
0, то между
переменными имеется слабая корреляционная
связь (рис.16.3). Для независимых переменных
коэффициент линейной корреляции равен
нулю.

Оценить существенность коэффициента линейной корреляции между случайными переменными по критерию Стьюдента можно при условии, что распределения этих случайных величин подчиняется нормальному закону и что они имеют совместное двумерное нормальное распределение.
Коэффициент линейной корреляции является случайной величиной, и поэтому для него может быть вычислена стандартная ошибка
![]() По
статистическим таблицам находим
критическое значение коэффициента
линейной корреляции.
По
статистическим таблицам находим
критическое значение коэффициента
линейной корреляции.
В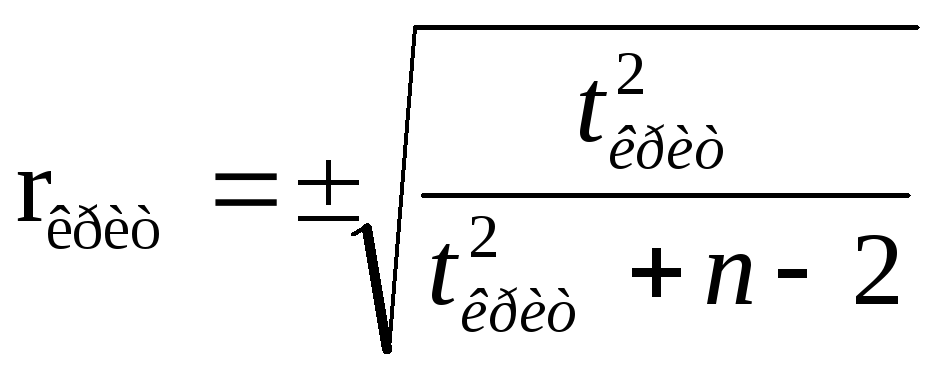 случае, если значение коэффициента
линейной корреляции, по абсолютной
величине не меньше 0,8, то можно ожидать
наличие между переменными линейной
зависимости и в уравнения регрессии
вводить сами факторы в первой степени.
Если значение коэффициента линейной
корреляции по абсолютной величине лежит
в диапазоне от критического значения
до 0,8, то в уравнения регрессии
рекомендуется вводить сравнительно
несложные функции от факторов.
Если значение
коэффициента линейной корреляции по
абсолютному значению меньше критического,
то такие факторы рекомендуется не
включать в уравнения регрессии.
случае, если значение коэффициента
линейной корреляции, по абсолютной
величине не меньше 0,8, то можно ожидать
наличие между переменными линейной
зависимости и в уравнения регрессии
вводить сами факторы в первой степени.
Если значение коэффициента линейной
корреляции по абсолютной величине лежит
в диапазоне от критического значения
до 0,8, то в уравнения регрессии
рекомендуется вводить сравнительно
несложные функции от факторов.
Если значение
коэффициента линейной корреляции по
абсолютному значению меньше критического,
то такие факторы рекомендуется не
включать в уравнения регрессии.
