
- •1. Основные определения. Технология моделирования
- •2. Методология моделирования
- •3. Анализ моделируемой системы и постановка задач
- •4.Второй этап моделирования. Формализация. Решение Задачи. Выбор метода моделирования
- •5. Корреляционный анализ
- •6.Третий этап моделирования. Разработка имитационных моделей.
- •7.Генерация равномерно-распределенных случайных чисел. Оценка их качества на тестах (по книге).
- •Тест частот
- •8.Планирование имитационных экспериментов. Концепция «черного ящика» Планирование экспериментов
- •9.План дфэ (дробных факторных экспериментов).
- •10. Рцкп (ротатабельный центральный композиционный план).
- •12.Тактическое планирование имитационных эксперементов
- •14.Основные свойства системы Arena.
- •15. Кластерный анализ. Евклидово расстояние. Ближайший сосед. Наиболее удаленный сосед. По среднему значению. Расстояние Хемминга.
- •1. Фр, фп, мпф, Равномерный экспоненциальный закон.
- •2. Метод моментов. Равномерный закон.
- •Метод моментов для равномерного закона
- •3. Метод моментов. Нормальный закон.
- •4. Метод моментов. Экспоненциальный закон.
- •5. Метод моментов. Гиперэкспоненциальный закон.
- •Решим полученное квадратное уравнение.
- •6. Метод моментов. Специальный эрланговский закон.
- •7. Метод обратной функции. Достоинства и недостатки.
- •Достоинства и недостатки аналитического метода генерации случайных чисел
- •8. Табличный метод генерации случайных чисел. Достоинства и недостатки.
- •9. План пфэ (полного факторного эксперимента).
- •10. План оцкп (ортогональный центральный композиционный план).
- •12. Применение дисперсионного анализа для оценки качества уравнений регрессии. Оценка значимости коэффициентов полинома.
- •13. Метод оптимизации по системе ур-й в частных производных.
- •14. Геометрический метод для 2 факторов.
- •15. Метод Ньютона.
- •1. Временные динамические ряды. Основные понятия. Проверка гипотез о существовании тенденций. Временные ряды
- •2. Сглаживание и прогнозирование методом скользящих средних. В чем смысл введения взвешиваний.
- •Сглаживание
- •Метод скользящих средних
- •Взвешенные скользящие средние
- •3. Сглаживание и прогнозирование экспоненциальных средних
- •4. Прогнозирование на нейронных сетях Прогнозирование на нейронных сетях
- •5. Группировка. Общие понятия. Постановка задачи и технология проведения кластерного анализа.
14. Геометрический метод для 2 факторов.
Если требуется найти оптимальные значения всего двух факторов, то можно использовать геометрический метод оптимизации, отличающийся сравнительной простотой и наглядностью.
![]() Постановка
задачи оптимизации:
Постановка
задачи оптимизации:
Приравняем целевую функцию нулю и выразим все переменные через одну из них.
Представим преобразованные ограничения и целевую функцию в виде прямых линий.
Построим область допустимых решений (ОДР). Первая точка пересечения линии целевой функции с ОДР является точкой минимума; последняя – максимума.
Проверим выполнение неравенств в точках min (max). Если все неравенства выполняются делаем заключение о корректности полученных результатов.
15. Метод Ньютона.
Для решения
оптимизационных задач с нелинейными
функциями можно использовать метод
Ньютона (метод касательных). Метод
Ньютона требует, чтобы оптимизируемая
функция была дважды дифференцируема.
В экстремальной точке производная
функции
![]() равна нулю и корень уравнения
равна нулю и корень уравнения
![]() можно искать приближённо методом
касательных, который заключается в
построении последовательных приближённых
можно искать приближённо методом
касательных, который заключается в
построении последовательных приближённых
![]() ,
,
![]() следующим образом. В точке
следующим образом. В точке
![]() строится касательная и точка пересечения
касательной с осью абсцисс берётся в
качестве следующего приближения
строится касательная и точка пересечения
касательной с осью абсцисс берётся в
качестве следующего приближения
![]()
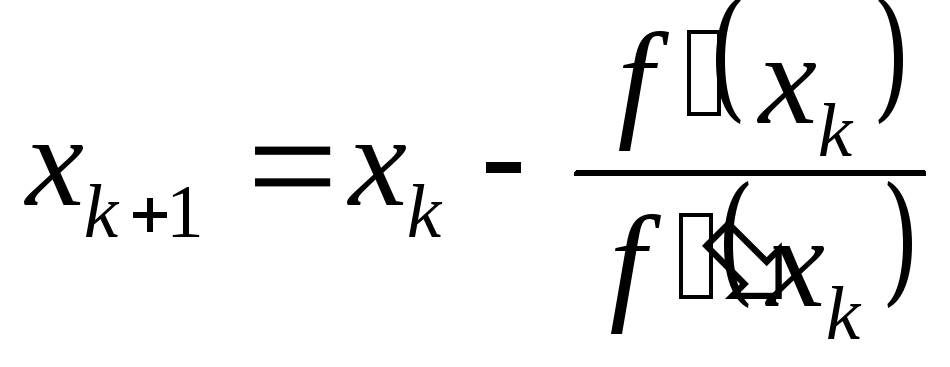
,
![]()
Вычисления
![]() по формуле продолжают до тех пор, пока
не выполнится неравенство
по формуле продолжают до тех пор, пока
не выполнится неравенство
![]() ,
после чего полагают что
,
после чего полагают что
![]() .Замечания:
.Замечания:
-
Если начальное приближение
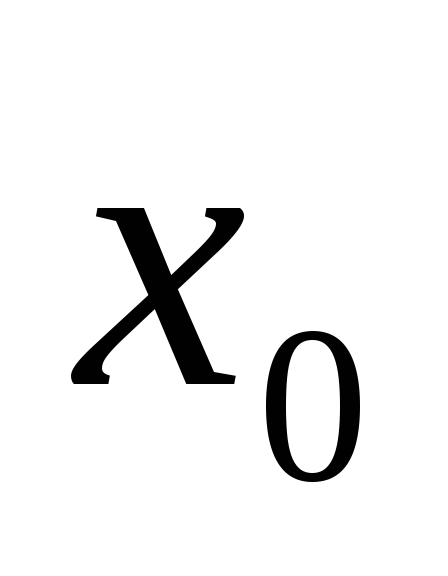 близко к
близко к
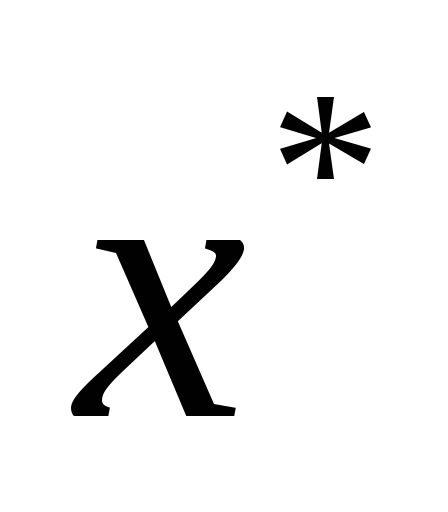 ,
то метод Ньютона обеспечивает быструю
сходимость в поиске экстремума.
,
то метод Ньютона обеспечивает быструю
сходимость в поиске экстремума. -
Если начальное приближение
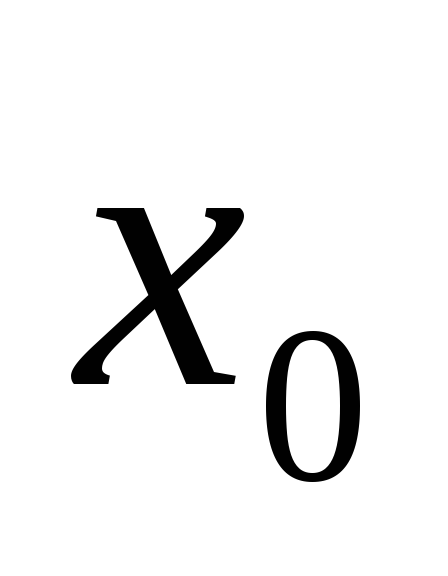 выбрано не достаточно близко, то для
поиска экстремума может потребоваться
значительное количество итераций, а в
принципе, неудачный выбор
выбрано не достаточно близко, то для
поиска экстремума может потребоваться
значительное количество итераций, а в
принципе, неудачный выбор
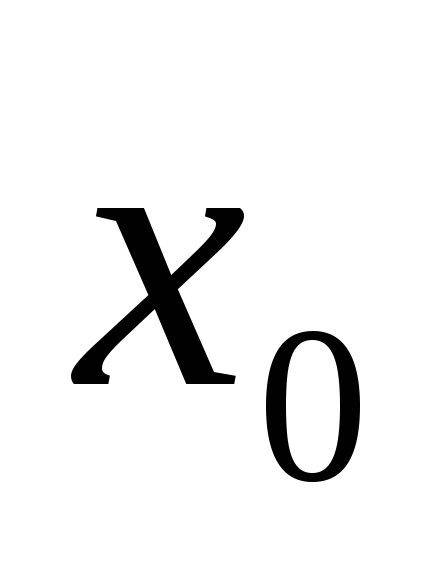 может привести к расходящемуся процессу,
т. е. мы будем удаляться от экстремальной
точки. Это возможно, если оптимизируемая
функция имеет нелинейность выше второй
степени.
может привести к расходящемуся процессу,
т. е. мы будем удаляться от экстремальной
точки. Это возможно, если оптимизируемая
функция имеет нелинейность выше второй
степени.
Для вычисления
шага изменения значения аргумента
![]() в итерационном процессе произведём
следующие преобразования:
в итерационном процессе произведём
следующие преобразования:
![]()
![]()
![]()
1. Временные динамические ряды. Основные понятия. Проверка гипотез о существовании тенденций. Временные ряды
Временными динамическими рядами (ВДР) называются статистические данные, отображающие развитие изучаемого процесса (явления) во времени.
В качестве фактора в ВДР используются либо даты, либо интервалы времени. В качестве отклика – количественные показатели развития изучаемого процесса во времени.
Основная цель статистического изучения временных динамических рядов (ВДР) состоит в выявлении и оценивании закономерностей их развития.
Основные показатели динамики ВДР
-
Базисный абсолютный прирост (спад) – вычисляется как разность между сравниваемым уровнем
 и уровнем, принятым за базу сравнения
и уровнем, принятым за базу сравнения
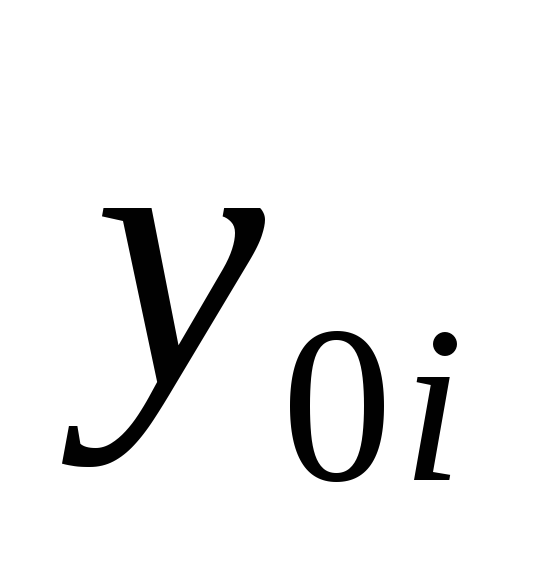 :
:
![]()
-
Цепной абсолютный прирост (спад) – вычисляется как разность между сравниваемым уровнем
 и уровнем, который ему предшествует:
и уровнем, который ему предшествует:
![]()
-
Базисный темп роста, вычисляется делением сравниваемого уровня на уровень, принятый за базу:
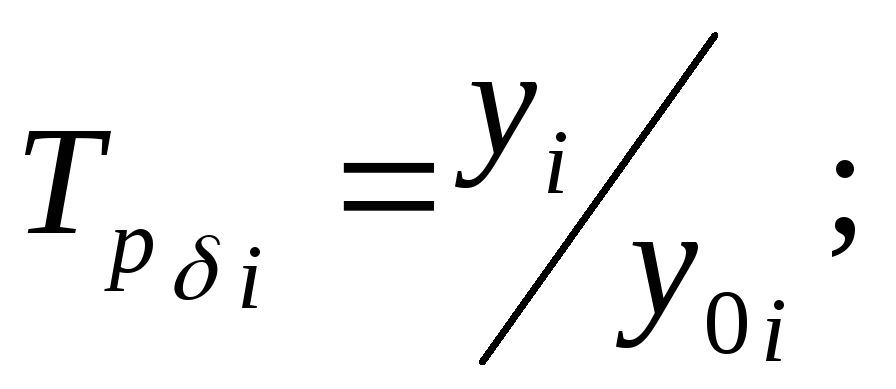
-
Цепной темп роста, вычисляется делением сравниваемого уровня на предыдущий:
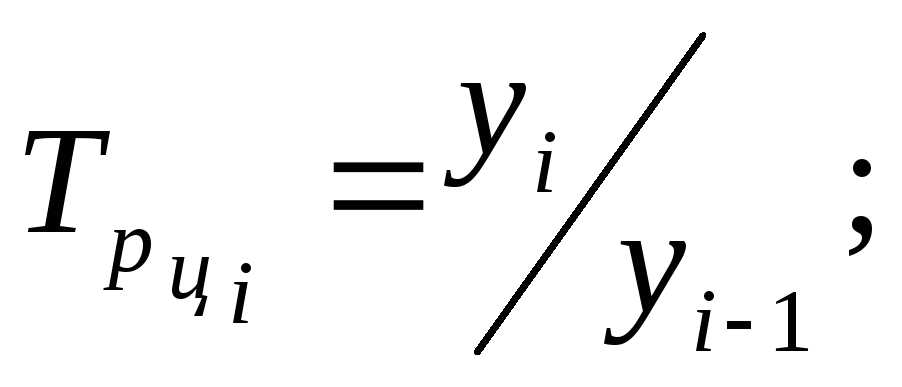
-
Базисный темп прироста – вычисляется делением базисного абсолютного прироста
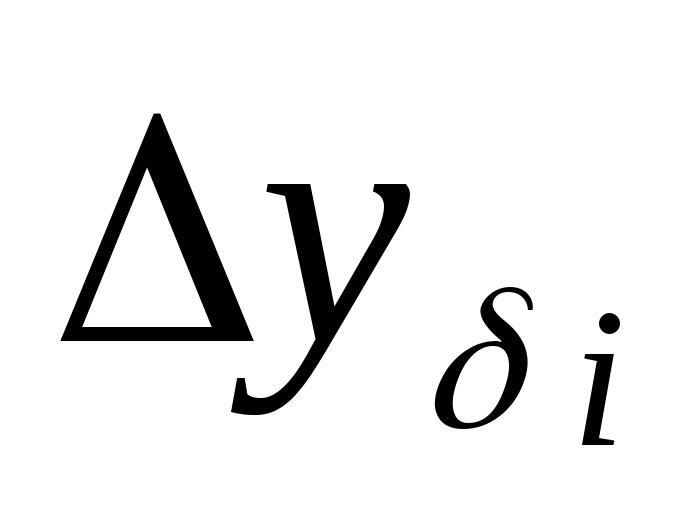 на уровень, принятый за базу сравнения:
на уровень, принятый за базу сравнения:
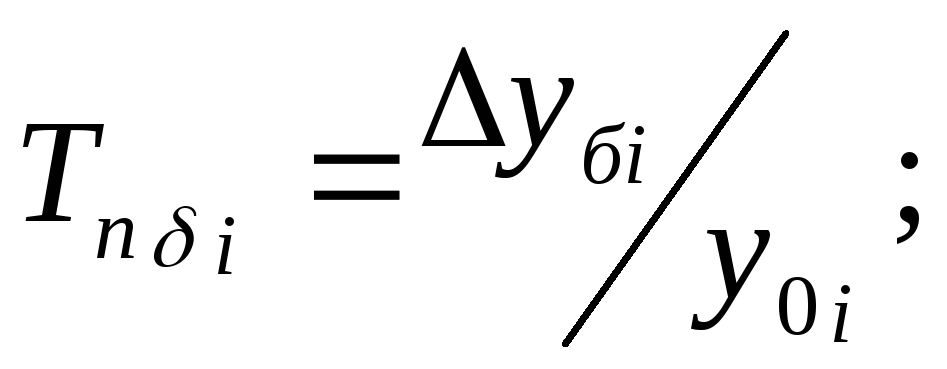
-
Цепной темп прироста – вычисляется как отношение сравниваемого цепного абсолютного прироста
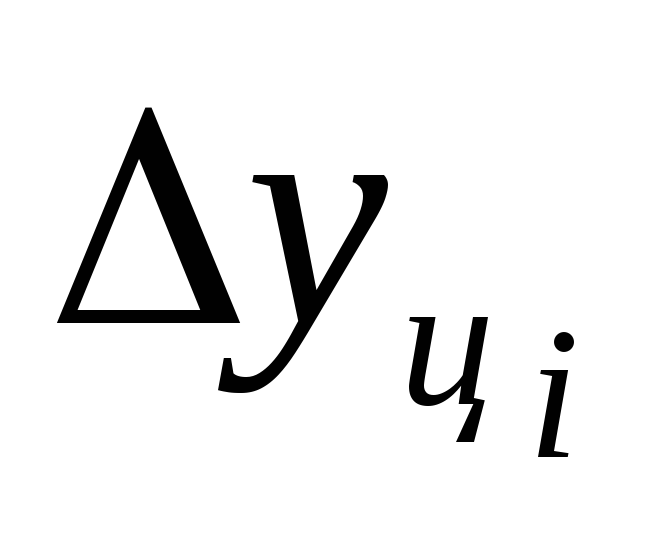 к предыдущему уровню:
к предыдущему уровню:
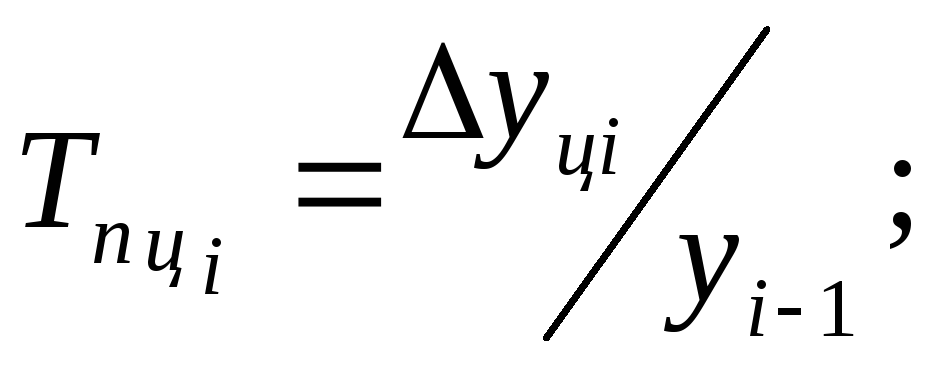
-
Средний уровень ВДР (оценка математического ожидания):
-
для интервального ряда:
![]()
-
для моментного ряда с равностоящими датами:
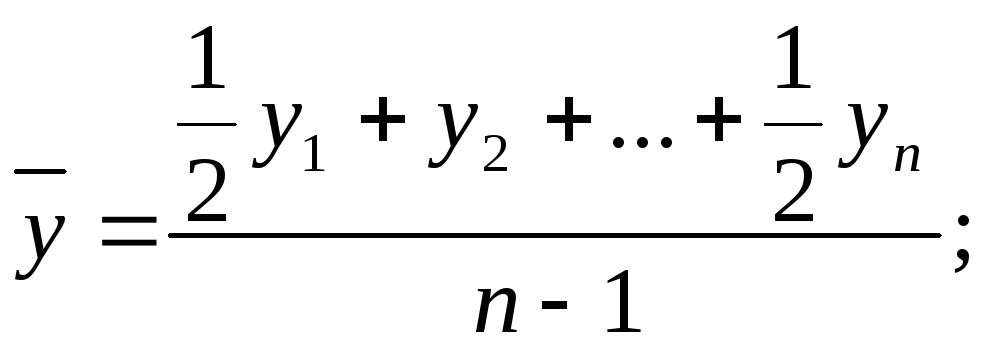
-
для момента ряда с неравностоящими датами:
![]()
-
Средний абсолютный прирост:
![]()
-
Средний темп роста:
![]()
-
Средний темп прироста:
![]()
Проверка гипотезы о существовании тенденции
Проверка разности средних уровней:
Разбиваем анализируемый ряд на две примерно одинаковые выборки, каждая из которых рассматривается как некоторая самостоятельная выборочная совокупность. Принимаем допущение, что выделенные выборки подчиняются нормальному закону (можно проверить в ППП Statistica). Воспользуемся методикой, разработанной для малых выборок.
Находим средние
значения для левой выборки
![]() и правой выборки
и правой выборки
![]() .
Примем допущение об однородности
дисперсий. Проверка производится по
F-критерию
Фишера
.
Примем допущение об однородности
дисперсий. Проверка производится по
F-критерию
Фишера
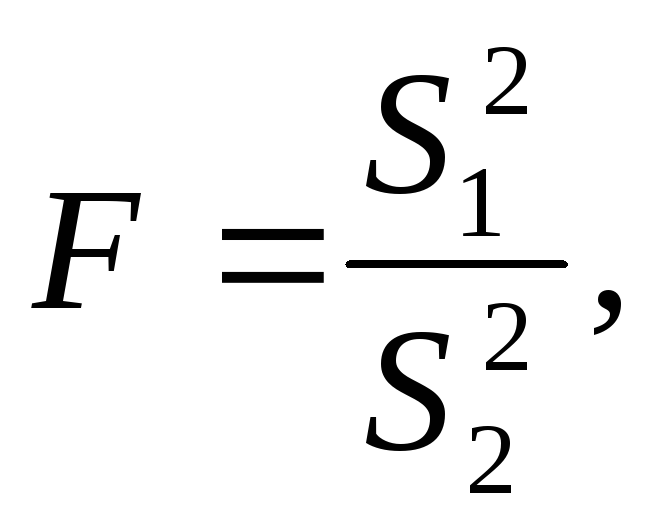 (где
(где
![]() )
)
число степеней
свободы
![]() и
и
![]() ;
;
Принимаем уровень
значимости по рекомендации
![]() ;
если
;
если
![]() ,
то гипотезу не отвергаем. В этом случае
можно проводить дальнейшую проверку.
Выдвигаем гипотезу о равенстве средних
и находим критерий Стьюдента:
,
то гипотезу не отвергаем. В этом случае
можно проводить дальнейшую проверку.
Выдвигаем гипотезу о равенстве средних
и находим критерий Стьюдента:
![]() ,
,
где S – среднее квадратическое отклонение разности средних.

При уровне значимости
![]() находим критическое значение критерия
Стьюдента для
находим критическое значение критерия
Стьюдента для
![]() количества
степеней свободы;
количества
степеней свободы;
Если
![]() ,
то гипотеза о равенстве средних
отвергается. В этом случае можно проводить
прогнозирование.
,
то гипотеза о равенстве средних
отвергается. В этом случае можно проводить
прогнозирование.
