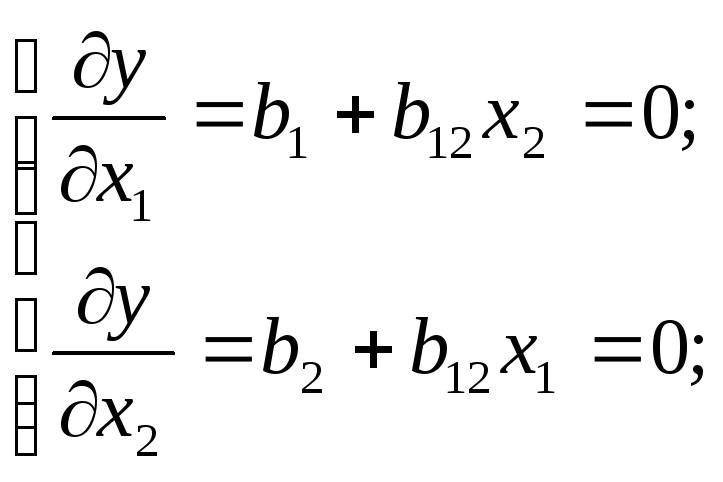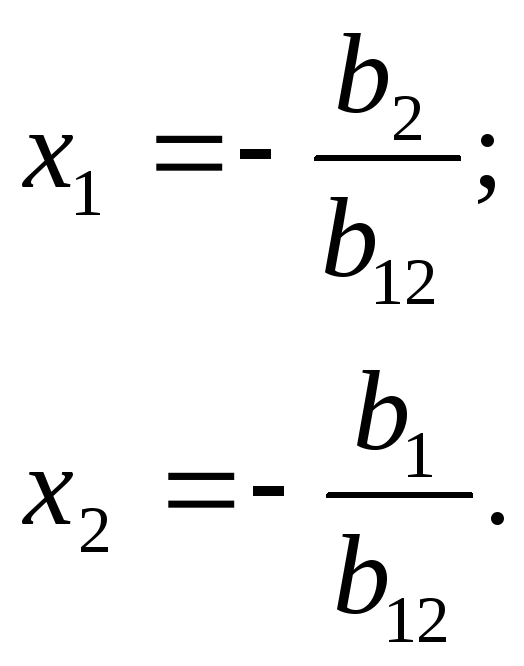- •1. Основные определения. Технология моделирования
- •2. Методология моделирования
- •3. Анализ моделируемой системы и постановка задач
- •4.Второй этап моделирования. Формализация. Решение Задачи. Выбор метода моделирования
- •5. Корреляционный анализ
- •6.Третий этап моделирования. Разработка имитационных моделей.
- •7.Генерация равномерно-распределенных случайных чисел. Оценка их качества на тестах (по книге).
- •Тест частот
- •8.Планирование имитационных экспериментов. Концепция «черного ящика» Планирование экспериментов
- •9.План дфэ (дробных факторных экспериментов).
- •10. Рцкп (ротатабельный центральный композиционный план).
- •12.Тактическое планирование имитационных эксперементов
- •14.Основные свойства системы Arena.
- •15. Кластерный анализ. Евклидово расстояние. Ближайший сосед. Наиболее удаленный сосед. По среднему значению. Расстояние Хемминга.
- •1. Фр, фп, мпф, Равномерный экспоненциальный закон.
- •2. Метод моментов. Равномерный закон.
- •Метод моментов для равномерного закона
- •3. Метод моментов. Нормальный закон.
- •4. Метод моментов. Экспоненциальный закон.
- •5. Метод моментов. Гиперэкспоненциальный закон.
- •Решим полученное квадратное уравнение.
- •6. Метод моментов. Специальный эрланговский закон.
- •7. Метод обратной функции. Достоинства и недостатки.
- •Достоинства и недостатки аналитического метода генерации случайных чисел
- •8. Табличный метод генерации случайных чисел. Достоинства и недостатки.
- •9. План пфэ (полного факторного эксперимента).
- •10. План оцкп (ортогональный центральный композиционный план).
- •12. Применение дисперсионного анализа для оценки качества уравнений регрессии. Оценка значимости коэффициентов полинома.
- •13. Метод оптимизации по системе ур-й в частных производных.
- •14. Геометрический метод для 2 факторов.
- •15. Метод Ньютона.
- •1. Временные динамические ряды. Основные понятия. Проверка гипотез о существовании тенденций. Временные ряды
- •2. Сглаживание и прогнозирование методом скользящих средних. В чем смысл введения взвешиваний.
- •Сглаживание
- •Метод скользящих средних
- •Взвешенные скользящие средние
- •3. Сглаживание и прогнозирование экспоненциальных средних
- •4. Прогнозирование на нейронных сетях Прогнозирование на нейронных сетях
- •5. Группировка. Общие понятия. Постановка задачи и технология проведения кластерного анализа.
12. Применение дисперсионного анализа для оценки качества уравнений регрессии. Оценка значимости коэффициентов полинома.
Дисперсионный анализ основан на разложении общей изменчивости результативного показателя на объяснённую дисперсию, которую удалось объяснить изменением переменных, вошедших в уравнение регрессии, и остаточную регрессию, которую объяснить не удалось. Для проведения дисперсионного анализа вычисляются.
-
Объяснённая сумма квадратов:
![]()
с количеством степеней свободы:
![]()
среднее значение суммы квадратов:
![]()
-
Остаточная сумма квадратов:
![]()
с![]() количеством степеней свободы:
количеством степеней свободы:
среднее значение суммы квадратов:
![]()
-
О
 бщая
сумма квадратов:
бщая
сумма квадратов:
![]()
с количеством степеней свободы:
Должно выполняться равенство:
![]()
-
Критерий Фишера
![]()
с количеством степеней свободы:
![]()
![]()
-
К
 оэффициент
множественной детерминации,
оэффициент
множественной детерминации,
с количеством
степеней свободы:
![]()
![]()
Показывает, какую часть изменения результативного показателя удалось объяснить изменением переменных, вошедших в уравнение регрессии.
Если вычисленные значения не меньше критических значений, то результаты аппроксимации признаются удовлетворительными.
-
Т
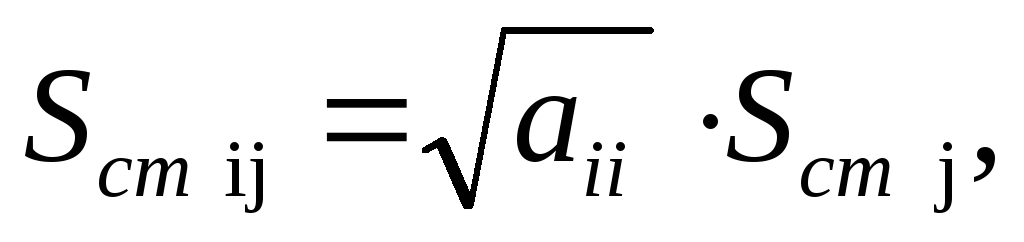 ак
как коэффициенты уравнения регрессии
вычисляются по случайным величинам,
то они и сами являются случайными
величинами. Поэтому можно вычислить
их стандартные ошибки и по ним определить
критерий Стьюдента и уровни их значимости.
ак
как коэффициенты уравнения регрессии
вычисляются по случайным величинам,
то они и сами являются случайными
величинами. Поэтому можно вычислить
их стандартные ошибки и по ним определить
критерий Стьюдента и уровни их значимости.
г![]() де
де
![]() -диагональный
элемент матрицы.
-диагональный
элемент матрицы.
чем
больше величина
![]() ,
тем лучше.
,
тем лучше.
Вычисляем критическое
значение критерия Стьюдента
![]() .
Если вычисленное значение
.
Если вычисленное значение
![]() превышает критическое, то считаем, что
уровень значимости
превышает критическое, то считаем, что
уровень значимости
![]() не превышает рекомендуемого значения
не превышает рекомендуемого значения
![]() ,
и поэтому вычисленные значения
коэффициентов приемлемы для отображения
экспериментальных данных. В противном
случае рекомендуется подобрать другие
значения переменных в аппроксимирующее
уравнение регрессии, в виде каких-либо
функций от аргументов.
,
и поэтому вычисленные значения
коэффициентов приемлемы для отображения
экспериментальных данных. В противном
случае рекомендуется подобрать другие
значения переменных в аппроксимирующее
уравнение регрессии, в виде каких-либо
функций от аргументов.
13. Метод оптимизации по системе ур-й в частных производных.
Постановка задачи оптимизации в общем случае сводится к максимизации или минимизации целевой функции с ограничениями на остальные функции и оптимизируемые факторы:
![]()
![]()
…
![]()
![]()
![]()
![]()
![]()
Наиболее простой случай, когда нет никаких ограничений. В этом случае применяется классический метод вычисления по решению системы в частных производных по оптимизируемым переменным.
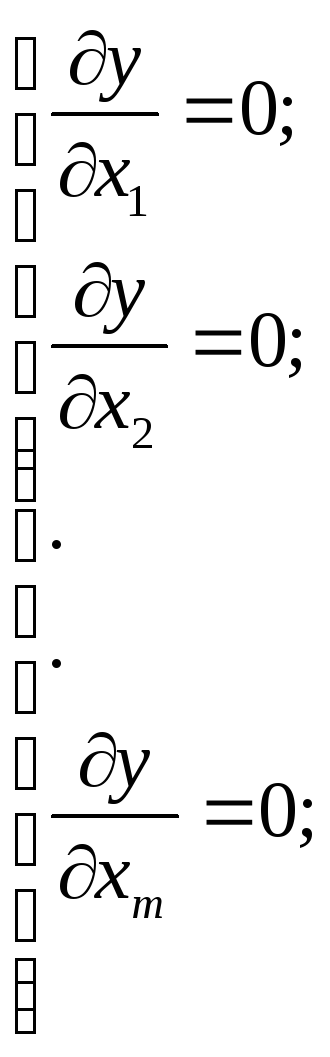
Рассмотрим двухфакторную математическую зависимость:
![]()
Вид экстремума определяется значением вторых частных производных:
![]()
![]()
![]()
-
Если
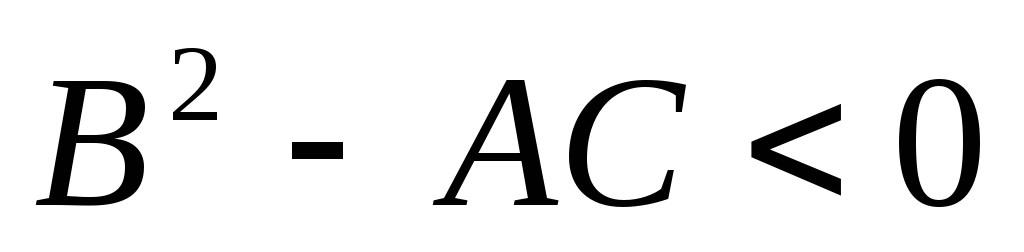 и
и
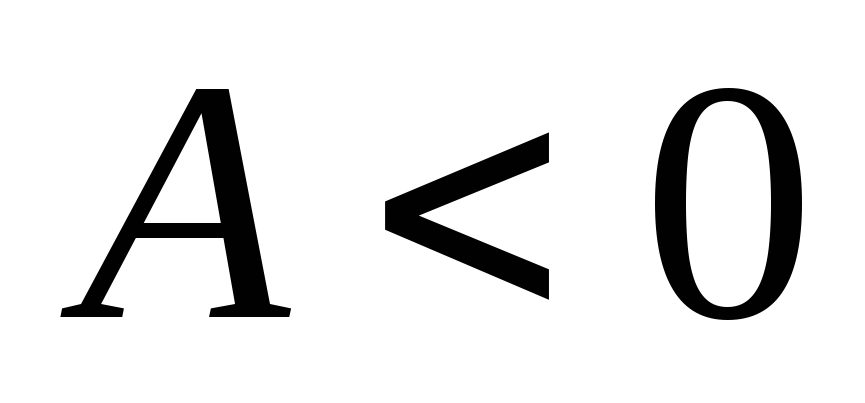 ,
то имеем максимум.
,
то имеем максимум. -
Если
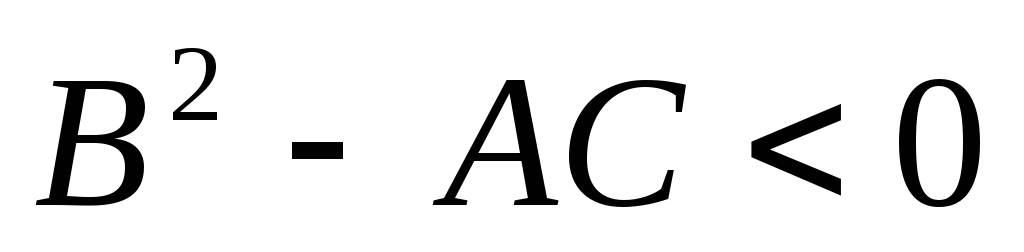 и
и
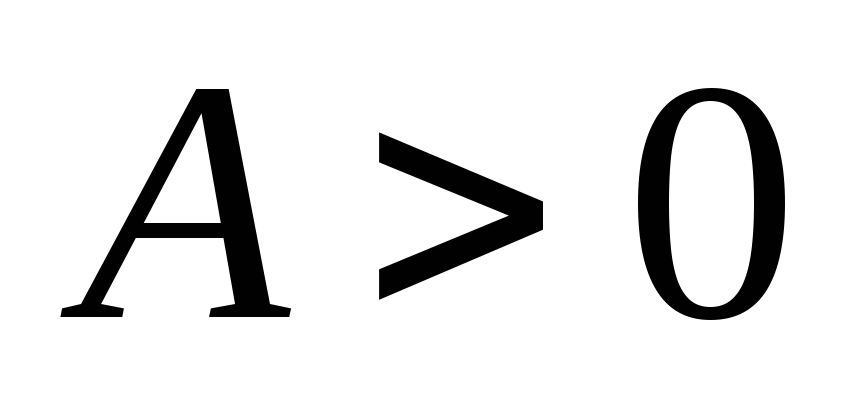 ,
то имеем минимум.
,
то имеем минимум. -
Если
 то нет ни мин, ни макс.
то нет ни мин, ни макс. -
Если
 ,
то экстремум может быть или не быть.
Требуется дополнительное исследование.
,
то экстремум может быть или не быть.
Требуется дополнительное исследование.
Рассмотрим частный случай двухфакторной функции:
![]()
Вычислим частные производные и координаты экстремальной точки: