Лекции по обыкновенным дифференциальным уравнениям Ржавинская Белякова Жаркова

Министерство образования и науки Российской Федерации Национальный исследовательский университет «МИЭТ»

Е.В. Ржавинская, Л.П. Белякова, Н.В. Жаркова

Лекции по обыкновенным дифференциальным уравнениям

Учебное пособие

Утверждено редакционно-издательским советом университета

Москва 2012

PDF created with pdfFactory Pro trial version www.pdffactory.com

Оглавление

Предисловие Глава 1. Дифференциальные уравнения первого порядка

1.1.Некоторые определения и примеры

1.2.Дифференциальные уравнения первого порядка, разрешенные относительно производной y'

1.3.Дифференциальные уравнения с разделяющимися переменными и приводящиеся к ним

1.4.Теорема существования и единственности решения задачи Коши для дифференциального уравнения dydx = f (x, y)

1.5.Простейшие типы дифференциальных уравнений, не разрешенных относительно производной

Глава 2. Метрические пространства

2.1.Аксиоматическое определение метрического пространства ..

2.2.Сходимость в метрических пространствах. Полнота

2.3.Принцип сжатых отображений

2.4.Доказательство теоремы о существовании и единственности решения задачи Коши для

уравнения dydx = f (x, y)

Глава 3. Дифференциальные уравнения порядка выше первого

3.1.Простейшие случаи понижения порядка

3.2.Линейные дифференциальные уравнения порядка n

3.3.Линейные однородные дифференциальные уравнения с постоянными коэффициентами

3.4.Линейные неоднородные дифференциальные уравнения

3.5.Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и правой частью специального вида

3.6.Метод вариации произвольных постоянных

Глава 4. Системы дифференциальных уравнений

4.1.Некоторые общие понятия

4.2.Интегрирование системы дифференциальных уравнений сведéнием к одному уравнению более высокого порядка

4.3.Системы линейных дифференциальных уравнений

4.4.Системы линейных однородных дифференциальных уравнений с постоянными коэффициентами

4.5.Метод вариации произвольных постоянных для систем дифференциальных уравнений

4.6.Устойчивость по Ляпунову. Классификация точек покоя

4.7.Исследование системы на устойчивость по первому приближению

Литература

5

PDF created with pdfFactory Pro trial version www.pdffactory.com

Предисловие

Дифференциальными уравнениями называются такие уравнения, в которых неизвестными являются функции одного или нескольких переменных, причем в уравнение входят не только сами функции, но и их производные. Если неизвестными функциями являются функции многих переменных, то уравнения называются уравнениями в частных произ- водных, а если рассматриваются функции только одного независимого переменного, то уравнения называются обыкновенными дифференциальными уравнениями.

Внастоящее время трудно представить область знания, претендующую на то, чтобы называться наукой, будь то химия, биология, медицина или маркетинг, если она не сталкивается с дифференциальными уравнениями. Дифференциальные уравнения поистине вездесущи.

Действительно, если некая модель отражает какое-то явление как процесс, т.е. рассматривает его во времени, то вместе с переменными величинами будут рассмотрены и скорости их изменения. Объединим их в уравнение - получим дифференциальное уравнение строго в соответствии с прозвучавшим выше определением.

Вданном пособии мы будем иметь дело только с обыкновенными дифференциальными уравнениями.

Глава 1 посвящена дифференциальным уравнениям первого порядка. Уравнения простых типов рассмотрены детально и строго.

Вглаве 2 представлены дифференциальные уравнения порядка выше первого. Основное внимание уделено теории линейных уравнений.

Глава 3 знакомит с метрическими пространствами. Здесь же доказывается теорема о существовании и единственности решения задачи Коши для дифференциального уравне-

ния dydx = f (x, y) .

Глава 4 посвящена системам дифференциальных уравнений. Подробно рассмотрены способы решения систем линейных дифференциальных уравнений, кратко изложены основные понятия теории устойчивости, разобрано несколько наглядных примеров.

Особое внимание в пособии (как и в курсе, который лег в его основу) уделено задаче Коши, на что авторы постоянно обращают внимание читателя. Для уравнения dydx = f (x, y)

формулировка теоремы о существовании и единственности решения задачи Коши приводится в главе 1, где анализируются условия теоремы, и доказывается в главе 3; для линейного уравнения порядка n и для систем ограничиваются только формулировкой (теоремы 3.1 и 4.1). Однако при доказательстве теорем 3.6, 3.7 и т.д. на протяжении всей главы 3 и в тексте постоянно подчеркивается: решается задача Коши. Не так навязчиво, но эта мысль проводится и в главе 4.

6

PDF created with pdfFactory Pro trial version www.pdffactory.com

Глава 1. Дифференциальные уравнения первого порядка

1.1. Некоторые определения и примеры

Определение 1.1. Уравнения, в которые неизвестная функция или вектор-функция входит под знаком производной или дифференциала, называются дифференциальными

уравнениями.

Пример 1.1. Материальная точка массой m движется под действием силы F, зависящей от времени t, положения точки, определяемого радиусом-вектором r(t), и ее скоростью

Пример 1.2. U(x, y, z) - потенциал электростатического поля, создаваемого системой зарядов с пространственной плотностью ρ(x, y, z). Функция U(x, y, z) удовлетворяет уравнению Пуассона:

∂2u + ∂2u + ∂2u = 4πρ(x, y, z) . ∂x2 ∂y2 ∂z2

Пример 1.3. Пусть по оси Ox движется точка и в каждый момент времени известна ее скорость f (t), f (t) - непрерывна.

Требуется найти закон движения точки, т.е. зависимость абсциссы движущейся точки

t

Функция ò f (τ) dτ удовлетворяет уравнению (1.1). Но уравнению (1.1) удовлетворяет

t0

также (при любом C) функция:

Для того чтобы в семействе (1.2) выделить одну конкретную функцию, нужно задать так называемое начальное условие, т.е. значение неизвестной функции x(t) при определенном значении аргумента, например:

7

PDF created with pdfFactory Pro trial version www.pdffactory.com

Решение уравнения (1.1), удовлетворяющее начальному условию (1.3), имеет вид

Предметом теории дифференциальных уравнений является построение методов нахождения неизвестных функций, определяемых дифференциальными уравнениями, а также изучение свойств этих функций.

Определение 1.2. Если в дифференциальном уравнении неизвестная функция или вектор-функция является функцией одного независимого переменного, дифференциальное уравнение называется обыкновенным дифференциальным уравнением.

Общий вид обыкновенного дифференциального уравнения

Если неизвестная функция, входящая в дифференциальное уравнение, является функцией двух или большего числа независимых переменных, то дифференциальное уравнение называется уравнением в частных производных (см. пример 1.2).

Определение 1.3. Порядком дифференциального уравнения называется наивыс-

ший порядок входящей в уравнение производной.

Определение 1.4. Функция y = φ(x) называется решением дифференциального уравнения, если после замены y на φ(x), y' на φ'(x), …, y(n) на φ(n)(x) получим тождество.

Процесс нахождения решения дифференциального уравнения называется интегриро-

ванием дифференциального уравнения.

1.2. Дифференциальные уравнения первого порядка, разрешенные относительно производной y'

Пусть

где f (x, y) - определена в некоторой области G плоскости xOy.

8

PDF created with pdfFactory Pro trial version www.pdffactory.com

Если y(x) - решение уравнения (1.6), то (1.6) устанавливает связь между координатами x и y любой точки (x, y) G и угловым коэффициентом касательной к графику решения y(x) в этой точке.

Определение 1.5. Поле направлений - совокупность отрезков (в малом) касатель- ных к графикам решений (1.6).

Определение 1.6. Совокупность точек плоскости, в которых угловой коэффициент касательной к графику решения (1.6) сохраняет одно и то же значение, называется изо-

клиной.

Уравнение изоклин: f (x, y) = k, k - произвольное вещественное число.

Пример 1.4. С помощью изоклин начертить приближенно графики решений уравнения

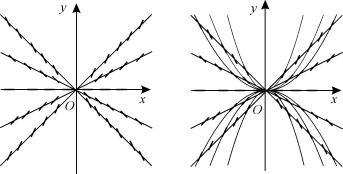
Уравнение (1.8) задает поле направлений всюду, за исключением оси ординат (x = 0). Схематично это поле изображено на рис.1.1,а, приблизительное поведение графиков решений - на рис.1.1,б.

Рис.1.1.

9

PDF created with pdfFactory Pro trial version www.pdffactory.com

Замечание. С геометрической точки зрения кажутся неестественными следующие два обстоятельства:

1)требуя, чтобы угловой коэффициент заданного в любой точке (x, y) G направления равнялся f(x, y), мы тем самым исключаем направления, параллельные оси Oy;

2)рассматривая только кривые, являющиеся графиками функций от x, мы исключаем из рассмотрения линии, которые прямыми, параллельными оси Oy, пересекаются более чем в одной точке.

В связи с этим обобщим предыдущую постановку задачи. Именно, будем допускать, что поле направлений в некоторых точках параллельно оси Oy. В этих точках угловой коэффициент по отношению к оси Ox теряет смысл (k = ∞), и мы заменим его угловым коэффициентом по отношению к оси Oy. Соответственно наряду c дифференциальным уравнением (1.6), рассмотрим уравнение

ла).

Определение 1.7. Линией называется множество точек (x, y) , задаваемых уравне-

Тогда каждая точка (x, y) лежит либо на участке линии, являющемся графиком непре- рывно дифференцируемой функции y(x), либо на участке линии, являющемся графиком не- прерывно дифференцируемой функции x(y).

тельно t (теорема об обратной функции): существует такая функция u, что t = u(x), u - непрерывна и непрерывно дифференцируема. Тогда y = ψ(u(x)), и y как функция от x непрерывна и непрерывно дифференцируема (теорема о сложной функции). В этом случае точка (x, y) лежит на участке линии, являющемся графиком непрерывно дифференцируемой функции от x.

10

PDF created with pdfFactory Pro trial version www.pdffactory.com

При таком определении понятия линии мы заранее требуем от решения уравнения (1.6) не только дифференцируемости, но и непрерывной дифференцируемости (см. 1.9). Только такие функции мы будем рассматривать в этом курсе.

Определение 1.8. Линии, имеющие в каждой точке (x, y) направление, задаваемое урав-

нениями (1.6) и (1.6'), называются интегральными кривыми, или интегральными линия-

ми уравнений (1.6), (1.6').

Задачу интегрирования дифференциального уравнения (1.6) мы поставим следующим образом: в области G найти все линии, имеющие в каждой точке направление, задаваемое уравнениями (1.6), (1.6').

Пример 1.5. С помощью изоклин приближенно начертить интегральные кривые дифференциального уравнения

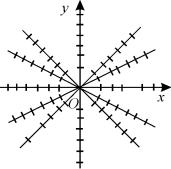
Если в (1.10') x' = 0, то y = 0, т.е. касательные к интегральным линиям параллельны оси Oy. Поле направлений схематически изображено на рис.1.2.

Рис.1.2.

11

PDF created with pdfFactory Pro trial version www.pdffactory.com

Интегральные кривые - окружности с центром в точке O(0,0) : x2 + y2 = c2 (решениями

этого уравнения будут функции y = c2 − x2 и y = −c2 − x2 , − c < x < c ).

Определение 1.9. Функцию ϕ(x, c) называют общим решением уравнения (1.6) в

области G , если при соответствующем выборе постоянной c функция ϕ(x, c) обраща-

ется в любое решение (1.6).

Определение 1.10. Уравнение Φ (x, y) = 0 интегральной линии дифференциального уравнения (1.6) и (1.6') называется интегралом дифференциального уравнения (1.6) и (1.6').

Определение 1.11. Уравнение Φ(x, y,c) = 0 называется общим интегралом диффе-

ренциального уравнения (1.6) и (1.6'), если при соответствующем выборе постоянной c оно задает любую интегральную линию дифференциального уравнения (1.6) и (1.6'), про- ходящую в области G .

1.3.Дифференциальные уравнения с разделяющимися переменными

иприводящиеся к ним

называются дифференциальными уравнениями с разделяющимися переменными. Функ-

ции f, g, M, N, P, Q будем предполагать непрерывными.

Для решения уравнений (1.11) и (1.12) нужно обе части этих уравнений умножить или разделить на такие выражения, чтобы в одну часть получившегося равенства вошла только независимая переменная x, а в другую - только y.

PDF created with pdfFactory Pro trial version www.pdffactory.com