Лекции по обыкновенным дифференциальным уравнениям Ржавинская Белякова Жаркова

cos 2x = P(x)eαx cosbx + Q(x)eαx sinbx .

Равенство имеет место, если α = 0, β = 2, P(x) = 1 и Q(x) = 0.

Частное решение дифференциального уравнения (3.80) ищем в виде

yч = (Acosbx + Bsinbx)x

(числа α ± iβ = ±2i являются корнями характеристического уравнения кратности r = 1 каж-

дый). Находим

y'ч = Acos 2x + Bsin 2x - 2Axsin 2x + 2Bxcos 2x ;

y''ч = −2Asin 2x + 2B cos 2x −

− 2Asin 2x − 4Axcos 2x + 2B cos 2x − 4Bxsin 2x ,

подставляем yч и y"ч в уравнение (3.80)

− 4Asin 2x − 4Bcos 2x − 4Axcos2x − 4Bxsin 2x +

+ 4Axcos 2x + 4Bxsin 2x = cos 2x ,

и, воспользовавшись линейной независимостью функций cos 2x и sin 2x на любом отрезке [a, b], приравниваем коэффициенты при cos 2x и sin 2x:

и yч = 14 xsin 2x .

Общее решение уравнения (3.80) записываем в виде

y = C1 cos2x + C2 sin 2x + 14 xsin 2x .

Отметим, что случай 2 содержится в случае 3 при α = p , β = 0 , а случай 1 - в случае 2 при p = 0 .

3.6. Метод вариации произвольных постоянных

Пусть дано линейное неоднородное дифференциальное уравнение

где pi (x), i = 1, 2,K, n и f (x) - непрерывные на отрезке [a, b] функции.

Пусть y1(x),K, yn (x) - фундаментальная система решений соответствующего линейного однородного уравнения

73

PDF created with pdfFactory Pro trial version www.pdffactory.com

Тогда по теореме 3.6

yобщ. одн = с1y1(x) + ... + сn yn (x) ,

где с1,...,сn - произвольные действительные постоянные.

Метод вариации постоянных для уравнения (3.81) заключается в том, что решение уравнения (3.81) ищется в виде

где с1(x),K,cn (x) - некоторые неизвестные функции.

Функция (3.83) должна удовлетворять одному уравнению - (3.81), а неизвестных функций в (3.83) - n, поэтому еще n − 1 условие на функции ci (x) можно наложить произвольно.

Воспользуемся этим произволом следующим образом. Имеем

y′(x) = c'1 (x) y1(x) + c1(x)y'1 (x) + ... + c'n yn (x) + cn y'n (x) =

Полагаем

n

åci′(x)yi′(x) = 0

i=1

и таким образом

n

y′′(x) = åci (x)yi′′(x)

i=1

и т.д., до производной порядка n –1:

74

PDF created with pdfFactory Pro trial version www.pdffactory.com

Так как y1(x), …, yn(x) - решение однородного уравнения (3.82), L[y1(x)] = 0, …, L[yn(x)] = 0, приходим к равенству

нений:

75

PDF created with pdfFactory Pro trial version www.pdffactory.com

Система (3.86) - система линейных алгебраических уравнений относительно неизвест-

изаписываем решение (3.81) в виде (3.83).

Пример 3.20. Проинтегрировать уравнение

Соответствующее однородное

y"+ y = 0 .

Его характеристическое уравнение: k2 +1 = 0 , характеристические корни: k1,2 = ±i ,

yобщ. одн = c1 cos x + c2 sin x .

Решение уравнения (3.87) ищем в виде

yобщ. неодн = c1(x)cos x + c2 (x)sin x .

Имеем

y′ = c1′(x) cos x + c1(x)(-sin x) + c2′ (x)sin x + c2 (x) cos x .

Полагаем

c1′(x)cos x + c′2(x)sin x = 0 .

Тогда

y′ = -c1(x) sin x + c2 (x) cos x

и y′′ = -c1′(x)sin x - c1(x)cos x + c2′ (x)cos x - c′2 (x)sin x .

Подставляем в уравнение (3.87) выражения для y, y', y":

- c1′(x)sin x - c1(x)cos x + c′2 (x)cos x - c2′ (x)sin x +

76

PDF created with pdfFactory Pro trial version www.pdffactory.com

+ c1(x)cos x + c2 (x)sin x = sin1 x .

Для неизвестных функций c1(x) и c2 (x) получим систему уравнений

Замечание. Отметим, что каким бы способом мы ни проинтегрировали линейное неоднородное дифференциальное уравнение, теорема 3.9 в структуре общего решения остается справедливой.

yобщ. одн = c3 cos x + c4 sin x ;

yч = −xcos x + (sin x)ln | sin x | .

Вфункции y(x) равенства (3.88) справа выписана сумма общего решения, соответствующего уравнению (3.87) однородного уравнения и некоторого его частного решения.

77

PDF created with pdfFactory Pro trial version www.pdffactory.com

Глава 4. Системы дифференциальных уравнений

Определение 4.1. Решением системы дифференциальных уравнений (4.1) называ-

ется n-мерная вектор-функция

при подстановке компонент которой во все уравнения системы (4.1) получим тождест- ва.

Теорема 4.1 (о существовании и единственности решения задачи Коши). Пусть функции fi(x, y1(x),…, yn(x)), i = 1, …, n:

1) непрерывны в области Q:

ì x0 - a £ x £ x0 + a

íîyi0 - bi £ y £ yi0 + bi , i =1, ..., n;

2) удовлетворяют условию Липшица по переменным y1, …, yn:

n

$N "i fi (x, y1,..., yn ) - fi (x, z1,..., zn ) £ Nå zk - yk .

k =1

78

PDF created with pdfFactory Pro trial version www.pdffactory.com

стве C с координатами x, y1, …, yn некоторую кривую, называемую интегральной кривой. При выполнении условий теоремы 4.1 через каждую точку пространства C проходит

единственная интегральная линия.

Возможна другая трактовка. В евклидовом пространстве с прямоугольными координа-

траектории, зависящей от параметра x. При таком подходе, уместном во многих физических и прикладных задачах, удобно считать x временем: x = t.

Система (4.1) перепишется в виде

(4.3) называется в этом случае динамической. Пространство с координатами y1, …, yn -

При любом фиксированном t динамическая система (4.3) определяет в пространстве y1, …, yn поле скоростей.

79

PDF created with pdfFactory Pro trial version www.pdffactory.com

æç f1(y1,K, yn ) ö÷

Если F(t, y) = ç L ÷ не зависит явно от t, то поле скоростей стационарно, т.е. не

çè fn ( y1,K, yn )÷ø

изменяется во времени. Процесс, описываемый системой дифференциальных уравнений (4.3), будет установившимся.

Пример 4.1.

Решением системы (4.4) является пара функций

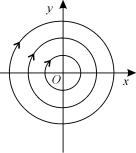
(убеждаемся в этом непосредственной подстановкой (4.5) в систему уравнений (4.4)). В данном случае фазовое пространство - плоскость xOy. Исключив из уравнений (4.5)

переменную t, получим x2 + y2 = C12 - семейство окружностей с центром в точке O (0, 0) - начале координат (рис.4.1).

Рис.4.1.

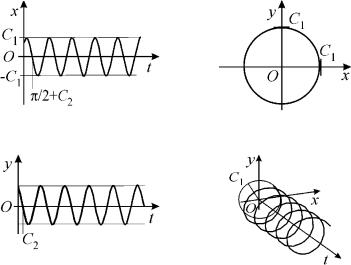
Зная фазовые траектории, можно составить представление о поведении интегральных линий в пространстве с переменными t, x, y (рис.4.2).

На рис.4.2,а и в приведены графики функций x(t) и y(t), которые даются формулами (4.5). Принимая во внимание окружности на плоскости xOy (рис.4.2,б), получаем примерную картину поведения интегральных линий в пространстве Otxy (рис.4.2,г).

80

PDF created with pdfFactory Pro trial version www.pdffactory.com

или

Уравнение (4.11) - линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами относительно компоненты y(t). Его характеристиче-

ское уравнение: k2 - 2k - 3 = 0 и корни k1 = 3, k2 = −1. Решение уравнения (4.11) имеет вид

y(t) = C1e3t + C2e–t.

Используя (4.10), находим x(t):

x(t) = 14 C1e3t + 14 C2e−t - 34 C1e3t + 14 C2e−t = - 12 C1e3t + 12 C1e−t .

Итак,

x(t) = - 12 C1e3t + 12 C1e−t ; y(t) = C1e3t + C2e−t

или

Обсудим теперь условия, при выполнении которых систему (4.6) можно свести к одному уравнению более высокого порядка.

82

PDF created with pdfFactory Pro trial version www.pdffactory.com