
Лекции по обыкновенным дифференциальным уравнениям Ржавинская Белякова Жаркова
.pdf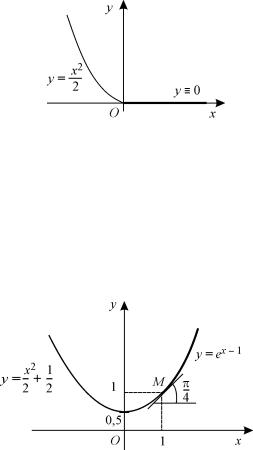
Например, интегральная линия уравнения (1.38) y = |
x2 |
( C = 0 ) и интегральная линия |
|
||
2 |
1 |
|
|
||
уравнения (1.39) y ≡ 0 (C3 = 0) имеют общую касательную в точке O(0, 0) (рис.1.6).
|
|
|
|
|
|
|
|
|
|
Рис.1.6. |
||
|
|
|
|
ì x2 |
|
|
|
|
|
|
||
|
|
|
|
ï |
|
|
x < 0 |
|
|
|
|
|
Функция y(x) = í |
2 , |
является интегральной линией уравнения (1.37). Или, на- |
||||||||||
|
|
|
|
ï |
0, |
x ³ 0 |
|
|
|
|
||
|
|
|
|
î |
|
|
|
|
||||
пример, y = |
x2 |
+ |
1 |
( C = |
1 |
) и y = ex−1 ( C = |
1 |
) в точке M (1,1) (рис.1.7). |
||||
2 |
2 |
|
1 |
|
2 |
|
3 |
|
e |
|||
|
|
|
|
|
|
|||||||
|
|
|
|
|
Рис.1.7. |
|
ì x2 |
+ |
1 |
, x <1 |
|
|
ï |
|
|
||
|
|
|
|||
Функция |
ï |
2 |
|
2 |
является решением уравнения (1.37). |
y(x) = í |
|
||||
|
ïex−1, |
|
x ³1 |
||
|
ï |
|
|
|
|
|
î |
|
|
|
|
Далеко не всегда уравнение (1.35) легко разрешить относительно y′ и еще реже полу-
ченные уравнения удается легко проинтегрировать, поэтому интегрировать уравнение вида (1.35) приходится также иными методами.
Случай 2. Уравнение (1.35) можно разрешить относительно y: |
|
||
|
|
y = f (x, y′) . |
(1.40) |
dy |
¢ |
|
|
Введем параметр p = dx = y |
и уравнение (1.40) запишется в виде |
|
|
|
|
||
|
|
y = f (x, p) . |
(1.41) |
23
PDF created with pdfFactory Pro trial version www.pdffactory.com
Возьмем полный дифференциал от обеих частей (1.41) и заменим dy на p dx, интегрируем и находим x = φ(p, c). Семейство решений исходного уравнения (1.40) находим в параметрической форме
ì x = j( p,c);
íîy = f (j( p,c), p).
Пример 1.12. Проинтегрировать дифференциальное уравнение
y = y¢2 + 2y¢3 .
Полагаем y' = p, тогда y = p2 + 2p3. Далее имеем
dy = (2 p + 6 p2 )dp ;
pdx = p (2 + 6 p)dp ;
dx = (2 + 6 p)dp .
Решение (1.42) в параметрической форме
ì |
|
|
2 |
+ C; |
|
ï x = 2 p + 3p |
|
. |
|||
í |
2 |
|
3 |
|
|
ï |
+ 2 p |
, при C ¹ 0, p ¹ 0 |
|
||
îy = p |
|
|
|
||
(1.42)
(1.43)
Ищем потерянные решения.
Делили на p, p = y' Þ y′ = 0 Þ y = C1 .
Уравнению (1.42) удовлетворяют функции y = C1 только при C1 = 0: y ≡ 0. Все решения уравнения (1.42) задаются равенствами
ì |
|
|
2 |
+ C |
|
ïx = 2 p + 3p |
|
, C Î R, p Î R. |
|||
í |
2 |
|
3 |
|
|
ï |
+ 2 p |
|
|
||
îy = p |
|
|
|
|
|
Решение y ≡ 0 входит в семейство (1.43) при p = 0.
Уравнение вида x = f (y, y') интегрируется тем же способом.
24
PDF created with pdfFactory Pro trial version www.pdffactory.com
Глава 2. Метрические пространства
2.1. Аксиоматическое определение метрического пространства
Определение 2.1. Пусть X - произвольное множество, x X , "y Î X задана одно-
значная действительная неотрицательная функция r(x, y) (каждой паре (x, y) поставле-
но в соответствие действительное число r(x, y) ), удовлетворяющая трем аксиомам:
1)r(x, y) = 0 Û x = y ;
2)r(x, y) = r( y, x) ;
3)r(x, z) £ r(x, y) + r( y, z) .
Пара (X , r) называется метрическим пространством, а элементы X - точками мет-
рического пространства.
Пример 2.1. X - множество действительных чисел. Расстояние между двумя действительными числами определено равенством
|
r(x, y) = | x - y | . |
|
||
Проверим выполнение аксиом. |
|
|
|
|
Аксиома 1. |
|
|
|
|
|
r(x, y) = 0 Þ | x - y | = 0 Þ x = y . |
|||
Обратно: |
x = y Þ | x - y | = 0 Þ r(x, y) = 0 . |
|
|
|
Следовательно, аксиома 1 справедлива. |
|
|
|
|
Аксиома 2. |
|
|
|
|
|
r(x, y) = 0 Þ | x - y | = | y - x | = r(y, x) . |
|||
Аксиома 2 выполняется. |
|
|
|
|
Аксиома 3. |
|
|
|
|
|
ρ(x, z) = | x − z | = | (x − y) + (y − z) | ≤ | x − y | + | y − z | = ρ(x, y) + ρ(y, z). |
|||
Аксиома 3 справедлива, и, таким образом, |
(X , r) - метрическое пространство. |
|||
Упражнение |
2.1. X - множество |
действительных чисел. Полагаем, что |
||
r(x, y) = arctg | x - y |. Показать, что (X , r) - метрическое пространство. |
||||
Пример 2.2. X - произвольное множество. Полагаем, что |
||||
|
r(x, y) = |
ì1, |
x ¹ y |
. |
|
í |
x = y |
||
|
|
î0, |
|
|
|
25 |
|
|
|
PDF created with pdfFactory Pro trial version www.pdffactory.com
Аксиомы 1 и 2, очевидно, выполняются.
Аксиома 3.
Случай 1. x = y = z. Имеем
ìr(x, y) = 0
ïír(x, z) = 0 Þ r(x, z) = r(x, y) = r(y, z)
ïîr( y, z) = 0
и r(x, z) = r(x, y) + r( y, z) .
Случай 2. x ¹ y, y = z Þ x ¹ z . По определению ρ
ìr(x, y) = 1
ïír(x, z) =1 Þ r(x, z) = 1 = r(x, y) + r(y, z) .
ïîr(y, z) = 0
Случай 3. y ¹ z, x = y (x ¹ z) . По определению ρ
ìr(x, y) = 0
ïír(x, z) = 1 Þ r(x, z) = 1 = r(x, y) + r(y, z) = 0 +1 = 1.
ïîr(y, z) = 1
Случай 4. x ¹ y, y ¹ z, x ¹ z .Тогда
ìr(x, y) = 1
ïír(x, z) = 1 Þ r(x, z) = 1 £ r(x, y) + r( y, z) .
ïîr(y, z) =1
Аксиома 3 выполняется во всех четырех случаях. Отсюда следует, что (X , r) - метри-
ческое пространство. Оно называется пространством изолированных точек.
Пример 2.3. X - множество Rn всех упорядоченных наборов n действительных чисел:
x = (x1,K, xn ) .
Полагаем, что для y = (y1,K, yn ) , r0 (x, y) = max | xk - yk | . |
|
||
|
|
1≤k ≤n |
|
Аксиома 1. |
|
|
|
r0 |
(x, y) = 0 Þ max | xk - yk |= 0 Þ |
|
|
|
|
1≤k≤n |
|
Þ $ i : max | xk - yk |= | xi - yi | = 0 Þ |
|
||
|
1≤k≤n |
1≤i≤k |
|
Þ "k , k =1,K,n ; | xk - yk |= 0 Þ x = y . |
|||
Обратно. |
|
|
|
Пусть x = y Þ |
|
|
|
Þ "k , k =1,K,n ; |
xk = yk |
Þ | xk - yk |= 0 Þ Þ r0 |
= max | xk - yk |= 0 . |
|
|
|
1≤k≤n |
26
PDF created with pdfFactory Pro trial version www.pdffactory.com
Аксиома 1 выполняется. Аксиома 2.
r0 |
(x, y) = 0 Þ max | xk - yk |= 0 = max | yk - xk |= r0 (y, x) . |
|
|
1≤k≤n |
1≤k≤n |
Следовательно, аксиома 2 выполняется. Проверим выполнение аксиомы 3. Имеем
r0 (x, z) = max | xk - zk |.
1≤k≤n
Но так как для любого z = (z1, …, zn)
| xk - zk | = | xk - yk + yk - zk | £ | xk - yk | + | yk - zk | ,
то, взяв max от обеих частей последнего неравенства, получим:
1≤k≤n
r0 |
(x, z) = max | xk - zk | £ max | xk - yk | + max | yk - zk | = |
||
|
1≤k ≤n |
1≤k ≤n |
1≤k ≤n |
= r0 (x, y) + r0 (y, z) .
Аксиома 3 справедлива, (X , r0 ) - метрическое пространство. Оно называется метри-
ческим пространством кортежей.
Пример 2.4. X - множество всех упорядоченных наборов n действительных чисел x = (x1,K, xn ) .
n
Полагаем, что r1(x, y) = å| xk - yk | .
k =1
Аксиома 1.
n
r1(x, y) = 0 Þ å| xk - yk | = 0 Þ
k=1
Þ"k, k = 1,K,n | xk - yk |= 0 и x = y .
Обратно.
Пусть x = y . Тогда
n
"k xk = yk Þ | xk - yk |= 0 Þ å| xk - yk | = 0 и r1(x, y) = 0 .
k =1
Аксиома 1 справедлива. Аксиома 2.
n |
n |
ρ1(x, y) = å| xk − yk | = å| yk − xk | = ρ1( y, x) . |
|
k=1 |
k=1 |
|
27 |
PDF created with pdfFactory Pro trial version www.pdffactory.com
Аксиома 2 выполняется. Аксиома 3.
n |
n |
ρ1(x, z) = å| xk − zk | = å| (xk − yk ) + (yk − zk ) | ≤ |
|
k =1 |
k =1 |
n |
n |
≤ å| xk − yk | + å| yk − zk | = ρ1(x, y) + ρ1( y, z) . |
|
k =1 |
k =1 |
Аксиома 3 выполняется. Следовательно, (X , r1) - метрическое пространство.
Замечание. Примеры 2.3 и 2.4 показывают, что один и тот же набор точек можно превратить в метрическое пространство разными способами (задав иначе расстояние - “метрику”).
Пример 2.5. X - множество всех непрерывных на отрезке [a, b] функций.
Полагаем r( f (x), g(x)) = max | f (x) - g(x) | .
a≤x≤b
Аксиома 1.
r( f , g) = 0 Þ max | f (x) - g(x) |= 0 .
a≤x≤b
По теореме Вейерштрасса
x0 [a,b] max | f (x) − g(x) |=| f (x0 ) − g(x0 ) | Þ
a≤x≤b
Þ x [a,b] | f (x) − g(x) | ≤ | f (x0 ) − g(x0 ) |= 0 Þ
Þ x [a,b] f (x) = g(x) .
Докажем обратное утверждение. Пусть f (x) = g(y) на отрезке [a, b] Þ
Þ x [a, b] | f (x) − g(x) |= 0
и, следовательно, r( f (x), g(x)) = max | f (x) - g(x) |= 0 .
a≤x≤b
Аксиома 1 справедлива.
Аксиома 2.
r( f (x), g(x)) = max | f (x) - g(x) |=
a≤x≤b
= max | g(x) − f (x) |= ρ(g(x), f (x)) .
a≤x≤b
Аксиома 2 выполняется.
Аксиома 3.
Пусть h(x) - непрерывная на отрезке [a, b] функция. По определению
28
PDF created with pdfFactory Pro trial version www.pdffactory.com

ρ( f (x), h(x)) = max | f (x) − h(x) |.
a≤x≤b
По теореме Вейерштрасса
x0 [a, b] max | f (x) - h(x) | = | f (x0 ) - h(x0 ) | ;
a≤x≤b
r( f (x), h(x)) = | f (x0 ) - h(x0 ) | = | f (x0 ) - g(x0 ) + g(x0 ) - h(x0 ) |£ £| f (x0 ) - g(x0 ) | + | g(x0 ) - h(x0 ) |£
£ max | f (x) - g(x) | + max | g(x) - h(x) |= |
|
a≤x≤b |
a≤x≤b |
= ρ( f (x), g(x)) + ρ(g(x), h(x)) .
Таким образом, и аксиома 3 справедлива и (X , ρ) - метрическое пространство. Его обозначают C[a, b].
Упражнение 2.2. X - множество всех непрерывных на отрезке [a, b] функций. Положим
b
r1( f (x), g(x)) = ò| f (x) - g(x) | dx .
a
Показать, что (X , r1) - метрическое пространство.
Докажем некоторые вспомогательные неравенства, которые дадут возможность расширить множество примеров метрических пространств.
Лемма 2.1. Пусть
u > 0 , v > 0 , p > 1, q сопряжено с p (т.е. 1p + 1q = 1),
тогда
uv £ |
u p |
+ |
vq |
. |
(2.1) |
|
p |
q |
|||||
|
|
|
|
Доказательство. Рассмотрим функцию y = xα , α > 0 .
При x > 0 y'(x) = axα−1 > 0 , т.е. y(x) монотонно возрастает, и по теореме об обратной
1
функции $ x = y α .
Далее имеем
y''(x) = a(a -1)xα−2 и ìy"> 0, при a >1,
íîy"< 0, при a <1
29
PDF created with pdfFactory Pro trial version www.pdffactory.com

следовательно, график функции выпуклый вниз при
α < 1.
Обозначим через S1 площадь, ограниченную графиком y = xα и прямой x = u, через S2 - площадь, ограниченную графиком x = y1/α и прямой y = v (рис.2.1,а, б).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.2.1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì |
|
|
|
u |
|
|
|
|
|
uα+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
= òxαdx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
ï |
S1 |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
a +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uα+1 |
|
vα |
+ |
|
|
|
|
|
|
|
|
||||||||
ï |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
Þ uv £ S1 + S2 |
£ |
+ |
|
|
|
. |
|
|
(2.2) |
||||||||||||||||||||
í |
|
|
v |
1 |
|
|
|
|
|
|
|
|
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a +1 |
1 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
ï |
|
|
|
|
|
|
|
|
|
|
vα |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+1 |
|
|
|
|
|
|
|||||||||||||||
|
= ò yα dv = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
ïS2 |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|||||||||||||||
|
1 |
|
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
ï |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пусть α + 1 = p, тогда q = |
1 |
|
|
+1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
В самом деле, |
|
1 |
+1 = |
a +1 |
= |
|
|
|
|
p |
|
|
, а так как p и q сопряженные ( |
1 |
+ |
1 |
= 1), то |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
p -1 |
p |
q |
||||||||||||||||||||||||||||||||||||||||
|
|
|
a |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
1 |
|
= 1 - |
|
|
1 |
|
= |
|
p -1 |
и q = |
|
p |
|
, или q = |
1 |
|
+1. |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
q |
|
|
|
p |
|
|
p |
|
|
|
|
|
a |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p -1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Итак, p = α+1, q = a1 +1, и, учитывая оценку (2.2), получаем:
uv £ u p + vq . p q
Неравенство (2.1) выполняется.
Лемма 2.2 (неравенство Гёльдера для сумм). Пусть a = (a1,…,an), b = (b1,…, bn), p > 1, q сопряжено с р ( 1p + 1q = 1). Тогда
n |
n |
1 |
n |
1 |
|
|
å| ak bk | £ (å| ak |p ) p (å| bk |q )q . |
(2.3) |
|||||
k =1 |
k =1 |
|
k =1 |
|
|
|
30
PDF created with pdfFactory Pro trial version www.pdffactory.com

Доказательство. Неравенство (2.3) однородно, т.е., если (2.3) выполняется для a и b, то λ μ - действительных чисел, оно выполняется для λ a и μ b.
В самом деле, λ a = (λ a1,…, λ an), μ b = (μ b1,…, μ bn). Пусть (2.3) справедливо для a и b.
Имеем
n |
n |
n |
|
å| l ak ×mbk | = å| l | ×| m | ×| ak ×bk | = | l | ×| m | å| ak ×bk | £ |
|||
k =1 |
k =1 |
k =1 |
(2.3) |
|
|||
|
|
n |
|
1 |
|
n |
|||||
£ | l | ×| m | (å| ak |p ) p (å| bk |q ) |
|||||||||||
(2.3) |
|
k =1 |
|
|
|
k =1 |
|||||
|
|
|
|
|
|||||||
|
n |
|
1 |
|
|
|
|
n |
|||
= (| l |p å| ak |p ) p (| m |q å| bk |q ) |
|||||||||||
|
k =1 |
|
|
|
|
|
|
|
k =1 |
||
|
n |
|
1 |
n |
|
1 |
|
||||
= (å| l ×ak |p ) p (å| m×bk |q )q |
|||||||||||
|
k =1 |
|
|
|
|
k =1 |
|
|
|
||
1
q
1
q
=
=
и неравенство (2.3) справедливо для λ a и μ b.
Следовательно, достаточно доказать (2.3) для a и b таких, что
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
å| ak |p = å| bk |q = 1. |
|
|
|
|
|
|
(2.4) |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
k =1 |
|
|
|
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
n |
n |
|
|
|
1 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
n |
n |
|
|
1 |
|
|
|
p |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
(Если å| ak |p = A , а å| bk |q = B , |
то |
|
å| ak |p = 1, |
|
|
å| bk |q = 1 |
и å |
|
|
|
ak |
|
=1, |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1/ |
p |
||||||||||||||||||||||||||||||||
|
|
|
|
k =1 |
k =1 |
|
|
|
|
|
A k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
B k =1 |
k =1 |
|
|
A |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
n |
|
|
|
1 |
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
å |
|
|
|
bk |
=1, и, доказав (2.3) для a и b, |
|
|
удовлетворяющих (2.4), в силу однородности |
|||||||||||||||||||||||||||||||||||
B |
1/ q |
|
|
||||||||||||||||||||||||||||||||||||||||
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(2.3), вместо a и b возьмем λ a и μ b, где l = |
|
|
|
|
и m = |
|
|
|
.) |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
1/ p |
|
|
1/ q |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Итак, пусть выполняется (2.4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Полагаем в лемме 2.1 u = |ak|, v = |bk| и получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| a |
k |
|p |
|
|
| b |q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
| a |
k |
×b |
| £ |
|
|
|
|
|
|
|
+ |
k |
. |
|
|
|
|
|
|
(2.5) |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
p |
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Просуммируем (2.5) по k = 1,…, n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
n |
|
|
|
n |
|
|
| a |
k |
|p |
|
|
n | b |q |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
å| ak ×bk | £ å |
|
|
|
|
|
|
+ å |
|
|
|
k |
|
|
|
= |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
k =1 |
|
|
|
k =1 |
|
|
|
|
|
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
1 |
n |
|
|
|
|
1 |
|
n |
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
= |
å| ak |p |
+ |
|
å| bk |q = |
+ |
=1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
p |
q |
p |
q |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
k =1 |
|
|
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
и для случая, когда выполняется (2.4), неравенство (2.3) справедливо. Лемма 22 доказана. При p = 2 получаем
31
PDF created with pdfFactory Pro trial version www.pdffactory.com

|
|
|
n |
|
|
|
|
|
åak bk £ |
||
|
|
|
k =1 |
|
|
æ |
n |
ö2 |
n |
n |
|
çç |
åak bk ÷÷ |
£ åak 2 |
× åbk |
2 |
|
èk =1 |
ø |
k =1 |
k =1 |
|
|
n |
|
|
n |
|
|
åak |
2 |
× åbk |
2 или |
||
k =1 |
|
|
k =1 |
|
|
- неравенство Коши - Буняковского.
Напоминание. Линейное пространство V = Rn превращается в евклидово, если задать скалярное произведение, например, как сумму попарных произведений одноименных
n
компонент (x, y) = å(xi × yi ) , и в нормированное, если положить || x ||= 
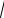 (x, x) .
(x, x) .
i=1
Вкурсе линейной алгебры было доказано неравенство Коши - Буняковского
|
|
|
(x, y) = || x ||2 ×|| y ||2 . |
||||||
Пример 2.6. |
X - |
множество всех |
упорядоченных наборов n чисел |
||||||
x = (x1,…, xn). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
||
|
|
r2 (x, y) = å(xk - yk )2 . |
|||||||
|
|
|
|
k =1 |
|
|
|
||
Аксиомы 1 и 2 очевидны. Проверим, выполняется ли аксиома 3: |
|||||||||
|
|
n |
n |
|
|
|
|||
|
r22 (x, z) = å(xk - zk )2 = |
å[(xk - yk ) + ( yk - zk )]2 = |
|||||||
|
|
k=1 |
k=1 |
|
|
|
|||
|
n |
|
|
|
|
|
|
|
|
|
= å[(xk - yk )2 + 2(xk - yk )(yk - zk ) + (yk - zk )2] = |
||||||||
|
k =1 |
|
|
|
|
|
|
|
|
|
n |
|
n |
|
|
|
|
n |
|
|
= å(xk - yk )2 + 2å(xk - yk )(yk - zk ) + å(yk - zk )2 £ |
||||||||
|
k =1 |
|
k =1 |
|
|
|
|
k =1 |
|
|
n |
|
|
|
|
|
|
|
n |
|
|
n |
|
|
n |
|
|
||
£ |
å(xk - yk )2 + 2 å(xk - yk ) å(yk - zk ) + å(yk - zk )2 = |
||||||||
Лемма 2.2 k =1 |
|
k =1 |
|
|
k =1 |
|
|
k =1 |
|
|
|
= (r2 (x, y) + r2 (y, z))2 . |
|||||||
Откуда получим |
|
|
|
|
|
|
|
|
|
|
|
r2 (x, z) £ r2 (x, y) + r2 (y, z) . |
|||||||
Аксиома 3 справедлива, следовательно, |
(X ,r2 ) - метрическое пространство. Оно на- |
||||||||
зывается n-мерным арифметическим евклидовым пространством Rn.
Лемма 2.3 (неравенство Гёльдера для интегралов). Пусть p > 1, q сопряжено с p,
функции f(x) и g(x) таковы, что существуют интегралы
b b
I1 = ò| f (x) |p dx и I2 = ò| g(x) |q dx и I1 ¹ 0 , I2 ¹ 0 .
a a
32
PDF created with pdfFactory Pro trial version www.pdffactory.com
