Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекции по обыкновенным дифференциальным уравнениям Ржавинская Белякова Жаркова

.pdf

Скачиваний:

176

Добавлен:

27.03.2016

Размер:

906.51 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 115 6 7 8 9 10 11 > Следующая >>>

в соответствующем пространстве R0n , R1n , R2n , в зависимости от того, какое из условий - (2.16), (2.17) или (2.18) - выполняется.

Замечание. Если число уравнений в системе (2.12) равно m < n, то принцип сжатых отображений неприменим.

Действительно, в этом случае ai j = 0, при i = m + 1, …, n, j = 1, …, n. cm+1, m+1 = K= cnn =1 , (C = −A + E) Þ

	n		n	n n
Þ max	å\| ckj \| ³1,	max	å\| ckj \| ³1,	ååckj2 ³1.
1≤k ≤n	j=1	1≤ j≤n k =1		k =1 j=1

Ни одно из условий сжатости не выполняется.

Пример.2.15. Методом итераций решить систему

					ìx - 2y = -2;		(2.19)
					í	2x + y = 2.	(2.19)
					î	2x + y = 2.
Матрица системы	æ1		-1ö		. Следуя обозначениям (2.13) - (2.15):
Матрица системы	A = ç			÷	. Следуя обозначениям (2.13) - (2.15):
	ç	2	1	÷
	è	2	1	ø

æ	0 2ö		æ x ö		;	æ	- 2ö		;
C = -A + E = ç		÷	; X = ç	÷	;	B = ç		÷	;
ç	- 2 0	÷	ç	÷		ç	2	÷
è	- 2 0	ø	è yø			è	2	ø

UX = CX + B =

æ 2y - 2

;

- 2x + 2

X (1)

1ö

;

X (2)

= UX (1)

- 2ö

;

X (3) =

æ- 2

; X (4) =

æ10ö

= ç

÷ .

0ø

0 ø

6 ø

Точное решение системы (2.19): x =

, или

æ2/ 5

. Последовательность

y =

точн

= ç

è6/ 5

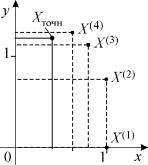
X (1) , X (2) , X (3) , X (4) , ... расходится (рис.2.6).

Рис.2.6.

PDF created with pdfFactory Pro trial version www.pdffactory.com

Достаточное условие не проверили:

	2
max	å\| ckj \| = 2 >1 в R0n ;	max
1≤k≤2	j=1	1≤ j≤2

2	n n
å\| ckj \| = 2 >1 в R1n ; ååckj2 = 8 >1 в R2n .
k=1	k=1 j=1

Ни одно из условий (2.16) - (2.18) не выполнятся, поэтому и последовательность итераций расходится.

Перепишем (2.19) в виде

ì 2x + y = 2

x +

y =

;

îx - 2y = -2

ï-

x +

y =

æ 1

A =

C = -A

;

1 1

÷ ;

+ E = ç

1 1

è 4

2 ø

æ 1

ö æ 1

x -

1 ö

÷æ x

÷ ç

UX = CX + B = ç

÷ç ÷ +

÷ = ç

÷ .

1 1

÷ç y

÷ ç

÷è ø

÷ ç

x +

è 4 2 ø

ø è 4

2 ø

Проверим достаточные условия:

1 ö

max

å| ckj | =

<1 в R0n ;

max

å| ckj | =

в R1n ; ååckj2 =

в R2n .

1≤k≤2

j=1

1≤ j≤2 k =1

k =1 j=1

Выполняются все три условия: (2.16) - (2.18) и последовательность

X (1)

æ1ö

X (2)

= UX (1) =

æ 1

;

÷ ;

è0ø

è 4 ø

æ13 ö

; X (4)

,…,

X (3) =UX (2) = ç16

= ç

è 8 ø

è 64 ø

сходится (рис.2.7).

Рис.2.7.

PDF created with pdfFactory Pro trial version www.pdffactory.com

Выбор первого элемента последовательности влияет на число итераций. Обычно в качестве первого приближения выбирают столбец свободных членов.

2.4.Доказательство теоремы о существовании

иединственности решения задачи Коши для уравнения dxdy = f (x, y)

Напомним формулировку теоремы.

Теорема 2.2. Пусть в уравнении

1)функция f (x,

2)функция f (x,

dy	= f (x, y)	(2.20)
dx

непрерывна в области G : ìx0 - a £ x £ x0 + a ;

íîy0 - b £ y £ y0 + b

удовлетворяет условию Липшица по y:

K x , "y1, y2 Î[y0 - b, y0 + b] | f (x, y1) - f (x, y2 ) | £ K | y1 - y2 | .

Тогда существует, и притом единственное в [x0 − h, x0 + h] , решение y = y(x) уравнения

(2.20), такое, что
y(x0) = y0,	(2.21)
где h ≤ min(a,b / M ,1/ K) , M = max \| f (x, y) \| .
(x, y) G

Доказательство. Рассмотрим C[x0 − h, x0 +h ] - совокупность всех функций y(x), опреде-

ленных и непрерывных на [x0 − h, x0 + h] с расстоянием

ρ(y(x), z(x)) =	max	z(x) - y(x)	.
ρ(y(x), z(x)) =	max	z(x) - y(x)	.
	[x0 −h, x0 +h]
	[x0 −h, x0 +h]

C[x0 − h, x0 +h ] - метрическое пространство (было доказано). Оно полно (примем без доказа-

тельства).

Дифференциальное уравнение (2.20) с начальным условием (2.21) заменим эквивалентным уравнением

x
y = y0 + ò f (x, y)dx .	(2.22)
x0

Справедливо следующее утверждение. Если f(x) интегрируема на отрезке [a, b], то

F(x) = ò f (t)dt непрерывна на отрезке [a, b].

Положим

PDF created with pdfFactory Pro trial version www.pdffactory.com

A(y) = y0 + ò f (x, y)dx .

Оператор A : C[x0 −h, x0 +h]

→ C[x0 −h, x0 +h] ставит в соответствие всякой функции y(x), не-

прерывной на [x0 − h, x0 + h ]

и не выходящей из области G, непрерывную функцию A(y),

график которой не выходит из области G, так как

A(y) − y0

ò f (x, y)dx

≤ ò

f (x, y)dx

≤ Mh < b ,

где M = max | f (x, y) | и, следовательно, y0 − b ≤ A( y) ≤ y0 + b .

Оператор A - сжимающий.

Действительно,

ρ(A( y), A(z)) =

max

+h]

ò f (x, y)dx − ò f (x, z)dx

[x0 −h,x0

Оценим

ò f (x, y)dx − ò f (x, z)dx

Имеем

ò f (x, y(x))dx − ò f (x, z(x))dx

≤

≤ ò

f (x, y(x)) − f (x, z(x))

dx ≤ K ò

y(x) − z(x)

dx .

Возьмем максимум от обеих частей:

ρ(A( y), A(z)) ≤ K

max

y(x) − z(x)

dx ≤ Khρ( y(x), z(x)) .

[x0 −h, x0 +h]

Выберем h так, чтобы Kh ≤ α < 1, тогда h <

и оператор A - сжимающий.

Так как C[x0 − h, x0 +h ] - полное метрическое пространство, существует, и притом единст-

венное, решение уравнения A(y) = y , т.е. единственное решение задачи Коши (2.20), (2.21). (Его можно найти методом итераций.)

Теорема 2.2 доказана.

PDF created with pdfFactory Pro trial version www.pdffactory.com

Пример 2.16. Найти методом итераций несколько приближений y1, y2, y3 к решению дифференциального уравнения

= x2

+ y2 , y(0) = 0 на G :

íì-1

£ x £1 .

î-1

£ y £1

Имеем

max(x2 + y2 ) = 2 ;

¶f

= 2y ; | 2y | £ 2

h = min(1,

) =

¶y

−1 ≤y ≤1

На рис.2.8 заштрихована область, в которой находим точное решение как предел итераций.

Пусть y0 º 0, тогда

= y (0) +

(x2

+ y 2 )dx =

;

= y (0) +

(x2 + y

2 )dx =

(x2 +

)dx =

;

= y

(0) +

(x2 + y

2 )dx =

(x2

+ (

)2 )dx =

+ 2

x11

x15

;

9×7

3×63×11

63×63×15

…

Рис.2.8. Рис.2.9.

Последовательность

º 0 ;

; y

+ ...; …

9×7

сходится к точному решению задачи Коши: y'= x2 + y2 , y(0) = 0 в области, заштрихован-

ной на рис.2.8. В данном примере уже первая итерация достаточно близка к точному решению (рис.2.9).

PDF created with pdfFactory Pro trial version www.pdffactory.com

Глава 3. Дифференциальные уравнения порядка выше первого

3.1. Простейшие случаи понижения порядка

Дифференциальное уравнение порядка n имеет вид:

¢	(n)	(x)) = 0 .	(3.1)
F(x, y(x), y (x),..., y

В некоторых случаях порядок уравнения может быть понижен, что обычно облегчает его интегрирование.

Случай 1. Дифференциальное уравнение не содержит искомой функции и ее производных до порядка k –1, т.е. имеет вид:

	F(x, y(k ) (x),..., y(n) (x)) = 0 .				(3.2)
Замена	æ x		®	x ö
Замена	y(k) (x) = z(x) понижает порядок ç		®	÷ .
	ç			÷
	è y(x)			z(x)ø
Пример 3.1. Проинтегрировать дифференциальное уравнение
	x2 y¢¢ = y¢2 .				(3.3)
Решение. Замена: y′(x) = z(x) . Тогда y′′ = z′		и уравнение (3.3) перепишется в виде
	x2 z¢ = z2 .				(3.4)

Уравнение (3.4) - первого порядка. Интегрируем уравнение (3.4). Это уравнение с разделяющимися переменными

= dx ;

- 1 = -

1 + C , или 1 = 1- C1x , откуда

z =

1- C1x

Возвращаемся к прежним переменным

y¢ =

;

(3.5)

1- C x

dy =

- C1x

(-C )(1 - C x)

и находим

y = -

x -

ln |1- C x | + C

C 2

Ищем потерянные решения.

PDF created with pdfFactory Pro trial version www.pdffactory.com

Интегрируя уравнение (3.5), мы делили на константу (- C1), т.е. потеряли семейство

решений: z	=	x , или y′ = x , или y =	x2	+ C .

		2		3

Разделяя переменные при интегрировании уравнения (3.4), делили на неизвестную z : y′ = 0 , т.е. y = C4 . Подставляя в исходное уравнение (3.3), убеждаемся, что это решение.

В процессе решения также делили на выражение (1- С1x) , т.е. x = 1 = C5 . Подставляем

в уравнение (3.3) и убеждаемся, что x = C5 решением не является.

Итак, все решения уравнения (3.3) - это двухпараметрическое семейство функций

y =	1	x -	1	ln \|1- C x \| + C
	C1		C 2
				1	2
		1

и два однопараметрических семейства	y =	x2	+ C	и	y = C	, C	3	Î R , C R .

	2		3		4			4

Случай 2. Дифференциальное уравнение не содержит независимой переменной x, т.е. имеет вид

F ( y(x), y′(x),..., y(n) (x)) = 0 .

(3.6)

В этом случае порядок уравнения можно понизить, взяв y за новую независимую переменную, а за новую неизвестную функцию y' = p(y):

æ	x		x	ö
ç		®		÷
ç		®	p(y)	÷ .
è y(x)			p(y)	ø
Пример 3.2. Решить уравнение
2 yy′′ = y′2 + 1 .				(3.7)

Решение. Замена: y' = p(y). По правилу дифференцирования сложной функции находим

y¢¢ =	dy′	=	dp(y)	=	dp dy	= p¢× p .
y¢¢ =	dx	=	dx	=	dy dx	= p¢× p .
Уравнение (3.7) принимает вид
		2 yp′p = p2 + 1 .				(3.8)

Порядок уравнения понижен.

Уравнение (3.8) является уравнением с разделяющимися переменными. Интегрируем данное уравнение

2 pdp	=	dy	;
p2 + 1		y

ln( p2 + 1) = ln | y | + ln C1 , C1 > 0 ;

PDF created with pdfFactory Pro trial version www.pdffactory.com

p2 + 1 = C2 y ,

где C2 = ±C1; C2 ¹ 0 .

Отсюда p = ±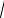C2 y -1 . Имеем два уравнения первого порядка:

1. y¢ =

2. y¢ = -

C2 y -1;

С2dy

C2 C2 y −

1 = dx

− C2 C2 y −1 = dx

Ответ:

= x + C .

Ответ:

y -1

C2 y -1 = x + C4.

Эти два ответа можно объединить формулой

= x + C

y -1

или

4(С2 y -1) = C22 (x + C5 )2 , C2 ¹ 0 ,

где C5 - любое действительное число. Потерянных решений нет.

Случай 3. Порядок дифференциального уравнения легко понижается, если удается преобразовать его к такому виду, что правая и левая части равенства являются полными производными от каких-либо функций.

Пример 3.3. Решить уравнение

¢ ¢¢¢

= 2 y

¢¢2

(3.9)

y y

Решение. Переписываем уравнение (3.9) в виде

y′′′

= 2

y′′

(3.10)

y¢¢

y¢

y′′′

¢¢

y′′

Замечаем, что

y¢¢ = (ln | y

| )

, а 2 y¢

= (2 ln | y

| )

. Тогда равенство (3.10) можно записать

как равенство полных производных: (ln | y′′ | )′ = (2 ln | y′ | )′ . Таким образом, функции ln | y′′ |

и 2 ln | y′ | отличаются на постоянную, т.е.

ln \| y′′ \| = 2ln \| y′ \| +lnC1 , C1 > 0 .	(3.11)
Порядок уравнения (3.10) понижен.
Потенцируем равенство (3.11)
\| y¢¢ \| = C1y¢2 или y¢¢ = C2 y¢2 , C2 ¹ 0 .	(3.12)
Опять применим тот же прием. Переписываем (3.12) в виде
50

PDF created with pdfFactory Pro trial version www.pdffactory.com

yy′¢′ = C2 y¢

и получаем

(ln | y′ |)′ = (C1 | y |)′ .

Откуда

ln \| y′ \| = C1 \| y \| +lnC3 , C3 > 0 .
Порядок уравнения (3.12) понижен.
Потенцируем
	y¢ = C4eC1y , C4 ¹ 0 .								(3.13)
Интегрируем уравнение (3.13)
				dy	= C4 dx .
					= C4 dx .
			eC1 y
Откуда
	-	1		e−C1y =C			4	x +C ,
	-			e−C1y =C				x +C ,
		C1						5
		C1
или
e−C1 y = (-C )(C								x + C ) ,
	1						4	5
или
eC6 y = C x + C ,
7	8
где - C1 = C6 ; C6 < 0 ; - C1C4 = C7 ; - C1C5 = C8 ; C7 , C8 - любые действительные числа.
Логарифмируя полученное выражение, получаем:
C6 y = ln \|C7 x + C8 \|.
Ищем потерянные решения:
1) y′′ = 0	Þ y′ = C9					Þ y = C9x + C10 ;			(3.14)
2) y′ = 0 Þ y = C . Последнее решение входит в семейство решений (3.14) при C9 = 0 .
Итак, все решения (3.10) задаются равенством C6 y = ln \| C7 x + C8 \|									и семейством решений

y = C9x + C10 .

Случай 4. Дифференциальное уравнение однородно относительно y, y′,..., y(n) , т.е. ес-

ли дифференциальное уравнение имеет вид F (x, y, y′,..., y(n) ) = 0 , то существует такое число α, что справедливо тождество

F(x, ky, ky′,..., ky(n) ) = k α F (x, y, y′,..., y(n) ) .

Вэтом случае говорят, что F - однородная функция порядка α по всем своим аргументам, начиная со второго.

PDF created with pdfFactory Pro trial version www.pdffactory.com

Порядок уравнения можно понизить заменой

y = e	ò z(x)dx	æ x	®	x	ö
y = e		:ç	®		÷ .
		ç			÷
		è y(x)		z(x)ø
Пример 3.4. Решить уравнение
yy′′ − ( y′)2 = 6xy2 .					(3.15)

Решение. Проверяем, что дифференциальное уравнение (3.15) однородно, переписывая его в виде:

yy′′ − ( y′)2 − 6xy 2 = 0 .

Имеем

F (x, y, y′, y′′) = yy′′ − ( y′)2 − 6xy 2 ;

F (x, ky, ky′, ky′′) = kyky′′ − (ky′)2 − 6x(ky)2 =

= k 2 ( yy′′ − ( y′)2 − 6xy 2 ) = k 2 F (x, y, y′, y′′) .

Функция F - однородная порядка α = 2.

Полагаем y = e

ò z(x)dx

Тогда

y¢ = e

ò z(x)dx

× z(x) ;

(3.16)

¢¢

¢ ¢

ò z(x)dx

× z

(x) + e

òz(x)dx

= (y )

= e

× z (x) .

Подставляем полученные выражения в (3.15)

2ò z(x)dx

×e

2ò z(x)dx

= 6x

×e

2ò z(x)dx

+ z ) - z

или

z2 + z¢ - z2 = 6x ,

или

z′ = 6x .

(3.17)

Порядок исходного уравнения понизили.

Интегрируем уравнение (3.17)

= 6x, Þ dz = 6xdx, Þ z = 3x2

+ C1

и возвращаемся к прежним переменным

y = e

ò(3x2

+C1 )dx

= e

x3 +C1x+C2

или

y = ex3 +C1x ×C3,

PDF created with pdfFactory Pro trial version www.pdffactory.com

<<< < Предыдущая 1 2 3 45 / 115 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.12.20184.09 Mб29Лекции 2011 ТМ и ТП.doc
#
13.08.20191.28 Mб15Лекции 5-7 Энергия в электростатике (полная вер...doc
#
14.08.20191.33 Mб12ЛЕКЦИИ АИС 1 ЧАСТЬ (ДО ОУ).doc
#
14.08.2019802.82 Кб10Лекции по АИС 2 часть.doc
#
03.09.20191.01 Mб12Лекции по диффурам.docx
#
27.03.2016906.51 Кб176Лекции по обыкновенным дифференциальным уравнениям Ржавинская Белякова Жаркова.pdf
#
15.04.20193.95 Mб15лекции по термеху.doc
#
24.08.2019139.78 Кб34Лекции С_Т_ЭКТ.doc
#
13.07.201987.04 Кб4Лекции ССиСК.doc
#
05.06.201524.5 Кб116Лекция 1. Теор фонетика.docx
#
27.03.201641.49 Кб5Лекция 1.docx