Лекции по обыкновенным дифференциальным уравнениям Ржавинская Белякова Жаркова

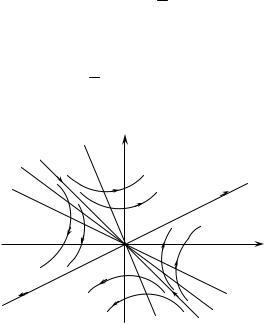
Отсюда α1 = –1; α2 = 12 . Получили прямые y = –x и y = 12 x.

Для того, чтобы узнать, какой из найденных кривых касаются интегральные кривые, строим изоклины:

y' = 0 Þ y = 14 x; y' = ∞ Þ y = 12 x; y' = 1 Þ y = 23 x.

Отметим, что интегральные кривые, попав в угол между решениями y = 12 x и y = 14 x

не могут оттуда выйти, так как там y' > 0, поэтому интегральные кривые касаются реше-

ния y = 12 x.

Примерное расположение траекторий для данной системы уравнений изображено на рис.4.5.

y = x/2

y = x/4

x

O

y = –x

y = 2x/3

Рис.4.5.

б) Случай k1 > 0, k2 > 0. Заменой t на –t сводим этот случай к уже рассмотренному случаю 1а. Траектории имеют такой же вид, как в случае 1а, однако с возрастанием t точки, сколь угодно близкие в начальный момент времени t = t0 к началу координат, удаляются из δ-окрестности начала координат. Точка покоя в этом случае не является устойчивой по Ляпунову.

Точка покоя рассмотренного типа называется неустойчивым узлом. Примерный вид траекторий изображён на рис.4.6.

103

PDF created with pdfFactory Pro trial version www.pdffactory.com

Пример 4.10. Исследовать точку покоя системы.

Дать чертеж расположения траекторий на плоскости xOy. Решение. Записываем характеристическое уравнение

или

k2 – 4k – 5 = 0.

Его характеристические корни: k1 = 5, k2 = – 1, точка покоя - седло.

Для выяснения того, какая траектория соответствует приближению к началу координат, решаем исходную систему.

или

105

PDF created with pdfFactory Pro trial version www.pdffactory.com

x(t) = 2C1e5t + C2e−t ; y(t) = C1e5t − C2e−t .

При C1 = 0 имеем x(t) = C2e−t ; y(t) = −C2e−t , отсюда xy = −1 и y = – x.

Таким образом, на фазовой плоскости при t → +∞ точка приближается к началу коор-

динат по прямой y = –x (а по прямой y = 2x удаляется от начала координат).

Расположение траекторий на фазовой плоскости изображено на рис.4.8.

y = –x

y = x/2

Рис.4.8.

Случай 2. Корни характеристического уравнения комплексные.

Пусть k1 = p + iq, k2 = p – iq; q ≠ 0. Тогда общее решение системы (4.43) имеет вид

x(t) = e pt (C1 cosqt + C2 sin qt) ; y(t) = e pt (C3 cosqt + C4 sin qt) .

Коэффициенты C3 и C4 выражаются линейно через C1 и C2.

а) Случай p < 0; q ≠ 0. Тогда lim e pt = 0 и, следовательно, функция ψ(t) = ept при t → +∞,

t →+∞

бесконечно малая, а так как при любом t | cos qt |≤1 и | sin qt |≤1, то найдется такое M, что при любом t справедливы оценки | C1 cos qt + C2 sin qt |≤ M и | C3 cos qt + C4 sin qt |≤ M . Отсюда сле-

дует, что x(t) и y(t) при t → +∞ являются бесконечно малыми (как произведение бесконечно малой функции на ограниченную).

чески устойчива. На фазовой плоскости траектории асимптотически приближаются к началу координат.

Точка покоя рассмотренного типа называется устойчивым фокусом.

б) Случай p > 0, q ≠ 0. Заменой t на –t сводим этот случай к уже рассмотренному случаю 2а. Траектории не отличаются от траекторий случая 2а, но движение по ним происходит в противоположном направлении.

106

PDF created with pdfFactory Pro trial version www.pdffactory.com

чальный момент времени t = t0 в сколь угодно малой окрестности начала координат, при стремлении t → +∞ удаляются к +∞.

Точка покоя в этом случае не является устойчивой по Ляпунову, она называется неус-

тойчивым фокусом.

Пример 4.11. Исследовать точку покоя системы дифференциальных уравнений и дать чертеж расположения траекторий на плоскости xOy.

Строим в точке (1,0) вектор скорости (x&, y&) = (y, - 2x + y) (1,0) = (0,-2) , что означает, что

возрастанию t соответствует движение по часовой стрелке. Так как фокус неустойчивый, траектории по часовой стрелке удаляются от начала координат.

Строим изоклины:

y' = 0 Þ y = 2x; y' = ∞ Þ y = 0, y' = 1 Þ y = y – x; x = 0.

Траектории на фазовой плоскости изображены на рис.4.9.

y

Рис.4.9.

107

PDF created with pdfFactory Pro trial version www.pdffactory.com

в) Cлучай p = 0; q ≠ 0. Общее решение имеет вид

x(t) = C1 cosqt +C2 sin qt ; y(t) = C3 cosqt + C4 sin qt .

На фазовой плоскости траектории - замкнутые кривые, окружающие начало координат (0,0). Точка покоя системы называется в этом случае центром.

Центр по определению является устойчивой по Ляпунову точкой покоя, так как

Иными словами, замкнутые траектории, точки которых в начальный момент времени лежат в ε-окрестности начала координат, не покидают этой ε-окрестности при t > t0.

Отметим, что асимптотической устойчивости нет, так как lim x(t) не существует.

t→+∞

Примерное расположение траекторий в случае центра приведено на рис.4.10.

y

Рис.4.10

Случай 3. Корни характеристического уравнения - кратные.

а) Случай k1 = k2 < 0. В этом случае характеристические корни не могут быть комплексными, так как комплексные корни входят сопряженными парами.

Общее решение имеет вид

108

PDF created with pdfFactory Pro trial version www.pdffactory.com

Точка покоя устойчива по Ляпунову и асимптотически устойчива, она называется, как и в случае 1а, устойчивым узлом. Расположение траекторий на фазовой плоскости приведено на рис.4.11.

При C2 = C4 = 0 это так называемый дикритический узел (рис.4.12).

Рис.4.11. Рис.4.12. Рис.4.13.

б) Случай k1 = k2 > 0. Заменой t на – t сводим этот случай к уже рассмотренному слу-

чаю 3а - неустойчивый узел (рис.4.13).

4.7. Исследование системы на устойчивость по первому приближению

Пусть дана система дифференциальных уравнений

Функции fi имеют непрерывные производные по xi, i = 1, …, n, в окрестности начала координат до второго порядка включительно.

Разлагаем функции fi(t, x1, …, xn) по формуле Тейлора в окрестности xi ≡ 0, i = 1, …, n, и

отбрасываем слагаемые порядка выше первого порядка относительно n 2

å xi i =1

Система (4.47) называется системой дифференциальных уравнений первого прибли-

жения для систем (4.45) и (4.46)).

109

PDF created with pdfFactory Pro trial version www.pdffactory.com

Исследуем точки покоя на устойчивость в случае, когда коэффициенты aij , i, j = 1, …,

n, - постоянные числа, т.е. система (4.45) стационарна в первом приближении. Достаточные условия устойчивости и неустойчивости в первом приближении даются

следующими двумя теоремами.

Теорема 4.6. Если система (4.45) стационарна в первом приближении и $N $a > 0 "T ³ t0 "Ri , i = 1,2,K, n , справедливо в достаточно малой окрестности начала ко-

ординат неравенство

и все корни характеристического уравнения системы (4.45) имеют отрицательные дейст-

Теорема 4.7. Если система (4.45) стационарна в первом приближении, функции Ri, i = 1, 2, …, n; удовлетворяют условиям теоремы 4.6 и хотя бы один корень характеристического уравнения системы (4.45) имеет положительную действительную часть, то точка

Отметим, что теоремы 4.6 и 4.7 не охватывают лишь так называемый критический слу-

чай: все характеристические корни ki имеют Reki £ 0 , причём хотя бы для одного корня

Reki = 0. В этом случае на устойчивость точки покоя системы (4.45) начинают влиять не-

линейные слагаемые остаточных членов и исследование на устойчивость, вообще говоря, невозможно.

Пример 4.12. Исследовать на устойчивость точку покоя системы.

Решение. Разлагаем по формуле Тейлора в окрестности точки O(0, 0) функции sin y и

ex.

и подставляем (4.49) в (4.48). Система (4.48) принимает вид:

110

PDF created with pdfFactory Pro trial version www.pdffactory.com

или

где порядок R1 и R2 выше первого относительно x2 + y2 .

Система первого приближения для системы (4.48) имеет вид

Ее характеристические корни: k1,2 = –2 ± i. Так как Re k1,2 = –2 < 0, то по теореме 4.6 точка покоя системы (4.48) асимптотически устойчива.

111

PDF created with pdfFactory Pro trial version www.pdffactory.com

Литература

1.Эльсгольц Л.Э. Дифференциальные уравнения и вариационные исчисления. - УРСС, 2002.

2.Колмогоров А.А., Фомин С.В. Элементы теории функций и функционального анализа. - М.: Наука, 1981.

3.Никольский С.М. Курс математического анализа. - М.: Физматлит, 2001.

112

PDF created with pdfFactory Pro trial version www.pdffactory.com