Лекции по обыкновенным дифференциальным уравнениям Ржавинская Белякова Жаркова

Подставляем Y в систему (4.32)

Имеем

Таким образом, общее решение системы (4.32)

Случай 3. Среди характеристических корней есть кратные. Пусть характеристический корень k = k1 имеет кратность r. Частные решения, входящие в фундаментальную систему решений и соответствующие корню k1, ищем в виде

Последние n – r слагаемых соответствуют остальным характеристическим корням k2, …, kn – r.

93

PDF created with pdfFactory Pro trial version www.pdffactory.com

Делим обе части на et и приравниваем коэффициенты при одинаковых степенях t

C3 = C1 - C2; C4 = C2.

Итак, решением системы (4.33) является пара функций

x(t) = C1et + C2tet; y(t) = (C1 – C2)et + C2tet

или вектор-функция

Описанный метод нахождения решения системы линейных однородных дифференциальных уравнений (4.25) носит название метода собственных векторов.

4.5. Метод вариации произвольных постоянных для систем дифференциальных уравнений

Пусть дана система линейных неоднородных дифференциальных уравнений

94

PDF created with pdfFactory Pro trial version www.pdffactory.com

или в краткой записи

где

Система соответствующих однородных уравнений

Пусть Y1(t), …, Yn(t) - фундаментальная система решений системы (4.37). Тогда (теорема

4.5)

Yобщ. одн = C1Y1(t) + … + CnYn(t),

где C1, …, Cn - произвольные действительные числа.

Метод вариации для систем заключается в том, что решение системы (4.35) ищется в виде

95

PDF created with pdfFactory Pro trial version www.pdffactory.com

Подставим (4.38) в (4.35) и получим

Вектор-функции Y1(t), …, Yn(t) - решения системы (4.37), поэтому

Равенство (4.39) примет вид

или

Система (4.40) - система линейных алгебраических уравнений относительно неизвест-

ных функций C1′(t),...,Cn′(t) с определителем

(Допустим, = 0. Обозначим через A матрицу, для которой = |A|. Если = 0, то rang(A) < n Þ столбцы A линейно зависимы. Это противоречит тому, что Y1(t), …, Yn(t) - фундаментальная система решений системы (4.37), следовательно, ≠ 0.)

Итак, ≠ 0, и система (4.40) имеет единственное решение

C1′(t),...,Cn′(t) .

96

PDF created with pdfFactory Pro trial version www.pdffactory.com

Это решение интегрируем, находим функции C1(t), …, Cn(t) и записываем решение системы дифференциальных неоднородных уравнений (4.35) в виде (4.38).

Пример 4.7. Проинтегрировать методом вариации постоянных систему

Общее решение соответствующей однородной системы уравнений

ìx& = y íîy& = -x

имеет вид

x(t) = C1 cos t + C2 sin t, y(t) = –C1 sin t + C2 cos t

(см. пример 4.3).

Варьируем постоянные. Сразу запишем систему уравнений (4.40) для данного случая

получаем

x(t) = (ln | sin t | + C4 ) cost + (t + C3 )sin t; y(t) = (ln | sin t | + C4 )(-sin t) + (t + C3) cost,

где C3 и C4 - произвольные действительные числа. В векторной форме

4.6. Устойчивость по Ляпунову. Классификация точек покоя

Пусть некоторый процесс описывается системой дифференциальных уравнений

с начальными условиями y1(t0) = y10, …, yn(t0) = yn0.

97

PDF created with pdfFactory Pro trial version www.pdffactory.com

Начальные условия обычно определяются из опыта и, следовательно, неизбежно содержат некоторые погрешности.

Если бы малые изменения начальных условий сильно влияли на решение, то решение, найденное по начальным условиям, не представляло бы никакого интереса, так как даже приближенно не описывало бы изучаемый процесс.

Для прикладных задач важным является вопрос: при каких условиях достаточно малые изменения начальных значений вызывают сколь угодно малые изменения решения?

Если рассматриваемые значения t Î[t0,+¥) , то этим вопросом занимается теория устой-

чивости.

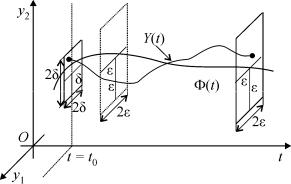
Геометрически в случае n = 2 устойчивость по Ляпунову означает, что все решения, мало отличающиеся в начальный момент времени t = t0 от Φ(t), не выйдут за пределы “трубы” около Φ(t) с квадратным сечением в любой следующий момент времени t > t0

(рис.4.3).

чивым.

98

PDF created with pdfFactory Pro trial version www.pdffactory.com

Пример 4.8. Исходя из определения, выяснить, устойчиво ли решение системы

ìdx = 4y,

ï dt

íï dy = -x

î dt

с начальными условиями x(0) = 0, y(0) = 0 .

Решение. Записываем соответствующее характеристическое уравнение

-k 4 = 0

-1 - k

или

k2 + 4 = 0 Þ k1, 2 = ±2i.

Решение системы ищем в виде

x(t) = α1 cos 2t + α2 sin 2t, y(t) = β1 cos 2t + β2 sin 2t.

Подставляя функции x(t) и y(t) в одно из уравнений системы, например, в первое, получаем:

–2α1 sin 2t + 2α2 cos 2t = 4β1 cos 2t + 4β2 sin 2t.

Отсюда

x(t) = a1 cos2t + a2 sin2t ; y(t) = a22 cos2t - a21 sin2t .

В векторной форме

Подставляем начальные условия

x(0) = a1 = 0 ; y(0) = a22 = 0 .

æ0ö

Таким образом, на устойчивость предлагается исследовать решение Φ(t) = ç ÷ .

çè0÷ø

Составляем разность Y(t) − Φ(t). При произвольном t она имеет вид

99

PDF created with pdfFactory Pro trial version www.pdffactory.com

æ0ö

и решение Φ(t) = ç ÷ устойчиво по Ляпунову.

çè0÷ø

Следует отметить, что оно не является асимптотически устойчивым, так как, например,

æç j1(t) ö÷

Исследование на устойчивость решения системы (4.41) Φ(t) = ç ... ÷ можно свести к

çèjn (t)÷ø

исследованию тривиального решения - “точки покоя”.

В самом деле, пусть xi = yi – φi(t). Тогда

Исследовать на устойчивость решение yi = φi(t), i = 1, 2, …, n, системы (4.41) означает исследовать решение xi ≡ 0, i = 1, 2, …, n, системы (4.42).

Перефразируем применительно к (4.42) определение устойчивости решения по Ляпунову.

Точка покоя xi = 0, i = 1, 2, …, n, системы (4.42) называется устойчивой по Ляпунову, если

ε > 0 δ = δ(ε) такое, что "xi (t), "t >t0

(| xi (t0 ) |< d Þ | xi (t) |< e, i =1,2,..., n ).

Иными словами:

100

PDF created with pdfFactory Pro trial version www.pdffactory.com

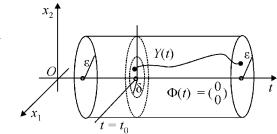
Для n = 2 (рис.4.4).

Рис.4.4.

Рассмотрим различные возможности расположения траекторий в окрестности точки

Случай 1. Характеристические корни действительны и различны. Пусть это числа k1 и k2. Тогда общее решение системы уравнений (4.33) имеет вид

Коэффициенты β1 и β2 линейно выражаются через α1 и α2.

Дальнейшее описание траекторий на фазовой плоскости проводим отдельно для нескольких случаев в зависимости от знаков k1 и k2.

а) Случай k1 < 0, k2 < 0. Пусть для определенности | k1| < | k2|.

101

PDF created with pdfFactory Pro trial version www.pdffactory.com

Тогда при t > 0

| x(t) | = | C1a1ek1t + C2b1ek2t | =

= ek1t | C1a1 + C2b1e(k2 −k1 )t | £ ek1t (| C1a1 | + | C2b1 |) .

Обозначим y(t) = ek1t (| C1a1 | + | C2b1 |) . Функция ψ(t) при t → +∞ бесконечно малая (как

произведение ограниченной функции на бесконечно малую ek1t ), тогда и x(t) тоже бесконечно малая при t → +∞ (теорема сравнения).

Аналогично y(t) при t → +∞ бесконечно малая функция.

Траектории системы двух линейных однородных дифференциальных уравнений с постоянными коэффициентами (4.43) на фазовой плоскости ведут себя следующим образом.

Все точки, находящиеся в начальный момент времени t = t0 в произвольной δ- окрестности начала координат, при достаточно большом t (t > T) переходят в точки, лежащие в сколь угодно малой ε-окрестности начала координат, а при t → +∞ стремятся к началу координат.

Точка покоя устойчива по Ляпунову и асимптотически устойчива. Точка покоя рассмотренного типа называется устойчивым узлом.

Пример 4.9. Исследовать точку покоя системы дифференциальных уравнений и дать чертеж расположения траекторий на плоскости xOy.