
- •Тема 1: Дифференциальные уравнения первого порядка §1. Некоторые определения и примеры
- •§2. Дифференциальные уравнения первого порядка, разрешенные относительно производной 𝑦’. Геометрическая интерпретация. Обобщение задачи.
- •§3. Дифференциальные уравнения с разделяющимися переменными и приводящиеся к ним.
- •§4. Теорема существования и единственности решения задачи Коши для дифференциального уравнения
- •§5. Простейшие типы дифференциальных уравнений, не разрешенных относительно производной.
- •Тема 2. Метрические пространства §1. Аксиоматическое определение метрического пространства. Примеры.
- •§2. Сходимость в метрических пространствах. Полнота.
- •§3. Принцип сжатых отображений.
- •§4. Теорема о существовании и единственности решения задачи Коши для дифференциального уравнения
- •§4.Теорема о существовании и единственности решения задачи Коши для уравнения .
- •Тема 3. Дифференциальные уравнения порядка выше первого. §1. Простейшие случаи понижения порядка.
- •§2. Линейные дифференциальные уравнения порядка n .
- •§3. Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
- •§4. Линейные неоднородные дифференциальные уравнения.
- •§6. Метод вариации произвольных постоянных.
Е.В. Ржавинская
Лекции по обыкновенным дифференциальным уравнениям
Весенний семестр 2010-2011 уч.года
Содержание:
Y
Тема 1: Дифференциальные уравнения первого порядка 3
§1. Некоторые определения и примеры 3
§2. Дифференциальные уравнения первого порядка, разрешенные относительно производной 𝑦’. Геометрическая интерпретация. Обобщение задачи. 5
§3. Дифференциальные уравнения с разделяющимися переменными и приводящиеся к ним. 8
§4. Теорема существования и единственности решения задачи Коши для дифференциального уравнения 14
§5. Простейшие типы дифференциальных уравнений, не разрешенных относительно производной. 17
Тема 2. Метрические пространства 21
§1. Аксиоматическое определение метрического пространства. Примеры. 21
§2. Сходимость в метрических пространствах. Полнота. 28
§3. Принцип сжатых отображений. 31
§4. Теорема о существовании и единственности решения задачи Коши для дифференциального уравнения 34
Тема 3. Дифференциальные уравнения порядка выше первого. 41
§1. Простейшие случаи понижения порядка. 41
§2. Линейные дифференциальные уравнения порядка n . 47
§3. Линейные однородные дифференциальные уравнения с постоянными коэффициентами. 55
§4. Линейные неоднородные дифференциальные уравнения. 60
§6. Метод вариации произвольных постоянных. 64
Тема 1: Дифференциальные уравнения первого порядка §1. Некоторые определения и примеры
Определение 1. Уравнения, в которые неизвестная функция или вектор - функция входит под знаком производной или дифференциала, называются дифференциальными уравнениями.
Пример
1. Материальная
точка массы m
движется под действием силы F, зависящей
от времени, положения точки, определяемого
радиусом - вектором r(t),
её скорости. По второму закону Ньютона
 или, так как
или, так как
 ,
,

Пример 2. U(𝑥, 𝑦, z) – потенциал электрического поля , создаваемого системой зарядов с пространственной плотностью ρ(𝑥, 𝑦, z). Функция U(𝑥, 𝑦, z) удовлетворяет уравнению Пуассона:
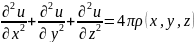
Пример
3.
Пусть по оси o𝑥
движется точка и в каждый момент времени
известна её скорость, пусть она равна
 ,
где
- непрерывна. Требуется найти закон
движения точки, то есть зависимость
абсциссы движущейся точки от времени.
Имеем:
,
где
- непрерывна. Требуется найти закон
движения точки, то есть зависимость
абсциссы движущейся точки от времени.
Имеем:
|
(1.1) |
Функция
 удовлетворяет (1.1), но уравнению (1.1)
удовлетворяет также при любом С
функция:
удовлетворяет (1.1), но уравнению (1.1)
удовлетворяет также при любом С
функция:
|
(1.2) |
Для того, чтобы в семействе (1.2) выделить одну конкретную функцию, нужно задать так называемое начальное условие, то есть значение неизвестной функции x(t) при определенном значении аргумента, например:
 .
(1.3)
.
(1.3)
Положим в (1.2) t = t0 и найдем:
|
|
Решение уравнения (1.1), удовлетворяющее начальному условию (1.3), имеет вид:
 .
(1.4)
.
(1.4)
Предметом теории дифференциальных уравнений является построение методов нахождения неизвестных функций, определяемых дифференциальными уравнениями, а также изучение свойств этих функций.
Определение 2. Если в дифференциальном уравнении неизвестная функция или вектор-функция является функцией одного независимого переменного, дифференциальное уравнение называется обыкновенным дифференциальным уравнением.
Общий вид обыкновенного дифференциального уравнения:
|
(1.5) |
Если же неизвестная функция, входящая в дифференциальное уравнение, является функцией двух или большего числа независимых переменных, дифференциальное уравнение называется уравнением в частных производных (как в примере 2).
Определение 3. Порядком дифференциального уравнения, называется наивысший порядок входящей в уравнение производной.
Определение
4.
Функция
𝑦=φ(𝑥),
называется решением дифференциального
уравнения, если после замены 𝑦
на φ(𝑥),
𝑦’
на φ’(𝑥),…у на
на
 (𝑥)
получим
тождество.
(𝑥)
получим
тождество.
Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения.
§2. Дифференциальные уравнения первого порядка, разрешенные относительно производной 𝑦’. Геометрическая интерпретация. Обобщение задачи.
Пусть
|
(2.1) |
где
 – определена в некоторой области G
плоскости 𝑥o𝑦.
– определена в некоторой области G
плоскости 𝑥o𝑦.
Если 𝑦(𝑥) - решение (2.1), то (2.1) устанавливает связь между координатами x и 𝑦 для любой точки(𝑥, 𝑦) ϵ G и угловым коэффициентом касательной к графику решения 𝑦(𝑥) в этой точке.
Определение 5. Поле направлений - совокупность отрезков (в малом) касательных к графикам решений (2.1).
Определение 6. Совокупность точек плоскости, в которых (угловой коэффициент) наклон касательной к графику решения (2.1) сохраняет одно и то же значение, называется изоклиной.
Уравнение изоклин: = k, k -произвольное вещественное число.
Пример 4. С помощью изоклин начертить приближенно графики решений уравнения:
|
(2.2) |
Перепишем (2.2) в виде:
|
(2.3) |
Полагаем


Уравнение (2.3) задаёт поле направлений всюду, за исключением оси ординат (𝑥=0). Схематично это поле изображено на рис.1, приблизительное поведение графиков решений на рис.2.

Рис. 1 Рис. 2
Замечание 1. С геометрической точки зрения кажутся неестественными следующие два обстоятельства:
1) требуя, чтобы угловой коэффициент заданного в любой точке (𝑥, 𝑦) ϵ G направления равнялся f(𝑥, 𝑦), мы тем самым исключаем направления, параллельные оси o𝑦;
2) рассматривая только кривые являющиеся графиками функций от 𝑥, мы исключаем из рассмотрения те линии, которые прямыми параллельными о𝑦 пересекаются более, чем в одной точке.
Поэтому несколько обобщим предыдущую постановку задачи. Именно, будем допускать, что поле направлений в некоторых точках параллельно оси о𝑦. В этих точках угловой коэффициент по отношению к оси о𝑥 теряет смысл (k=∞), и мы заменим его угловым коэффициентом по отношению к оси о𝑦. Соответственно этому наряду c дифференциальным уравнением (2.1), рассмотрим уравнение:
|
(2.1') |
где
 (f1=0
там и только там, где
не
имеет смысла)
(f1=0
там и только там, где
не
имеет смысла)
Определение 7. Линией называется множество точек (𝑥,𝑦), задаваемых уравнениями 𝑥=φ(t), 𝑦=ψ(t), t∊(a,b). Будем предполагать, что
1)
2)
|
(2.4) |
Тогда каждая точка (𝑥, 𝑦) лежит либо на участке линии, являющемся графиком непрерывно дифференцируемой функции 𝑦(𝑥), либо на участке линии, являющемся графиком непрерывно дифференцируемой функции 𝑥(𝑦).
Действительно, пусть t∊(a,b) и (φ'(t0))2 +(ψ'(t0))2 >0 ⇒хотя бы одно из слагаемых не равно нулю, пусть φ'(t0) ≠0 ⇒ ∃ε ∀t ϵ(t0–ε, t0+ε) φ'(t) сохраняет знак (например, если φ'(t0) >0, то ∀t ϵ(t0–ε, t0+ε) φ'(t)>0) ⇒ уравнение 𝑥=φ(t) можно разрешить относительно t (теорема об обратной функции): существует такая функция u, что t=u(𝑥), u - непрерывна и непрерывно дифференцируема. Тогда 𝑦=ψ(u(𝑥)) и 𝑦 как функция от 𝑥 непрерывна и непрерывно дифференцируема (теорема о сложной функции). В этом случае точка (𝑥,𝑦) лежит на участке линии, являющемся графиком непрерывно дифференцируемой функции от 𝑥.
При таком определений понятия линии мы заранее требуем от решения уравнения (2.1) не только дифференцируемости, но непрерывной дифференцируемости (см. 2.4). Только такие функции мы будем рассматривать в вашем курсе.
Определение 8. Линии, имеющие в каждой точке (𝑥,𝑦) направление, задаваемое уравнениями (2.1) и (2.1'), называются интегральными кривыми или интегральными линиями уравнений (2.1), (2.1').
Задачу интегрирования дифференциального уравнения (2.1) мы поставим следующим образом: в области G найти все линии, имеюшие в каждой точке направление, задаваемое уравнениями (2.1), (2.1').
Пример 5. С помощью изоклин приближённо начертить интегральные кривые дифференциального уравнения:
|
(2.5) |
Пусть 𝑦≠0. Присвоим производной 𝑦' несколько значений:




Функция
 теряет смысл при 𝑦=0 (на прямой 𝑦=0)
поэтому вместе c
(2.5) рассмотрим уравнение:
теряет смысл при 𝑦=0 (на прямой 𝑦=0)
поэтому вместе c
(2.5) рассмотрим уравнение:
|
(2.5') |
Если в (2.5') 𝑦=0, то 𝑥'=0, то есть касательные к линиям параллельны оси o𝑦.
Поле направлений схематически изображено на рис. 3.

Рис. 3
Интегральные
кривые - окружности с центром в точке
О(0, 0): 𝑥2+𝑦2=c2.
(Решениями же этого уравнения будут
функции
 и
и
 –с < 𝑥 < c).
–с < 𝑥 < c).
Определение 9. Функцию φ(𝑥, с) называют общим решением (2.1) в области G, если при соответствующем выборе постоянной c функция φ(𝑥, с) обращается в любое решение (2.1).
Определение 10. Уравнение Φ(𝑥, 𝑦)=0 интегральной линии дифференциального уравнения (2.1), (2.1'), называется интегралом дифференциального уравнения (2.1), (2.1').
Определение 11. Уравнение Φ(𝑥, 𝑦, c)=0 называется общим интегралом дифференциального уравнения (2.1), (2.1'), если при соответствующем выборе с оно даёт любую интегральную линию дифференциального уравнения (2.1), (2.1'), проходящую в области G.









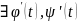 и непрерывны;
и непрерывны; .
.
