2. Понятие градиента
Градиент – вектор (набор) частных производных от функции по ее аргументам:
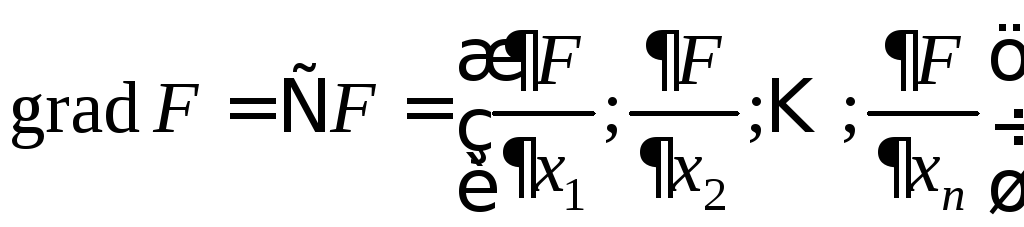
Градиент как вектор, вычисленный в точке, показывает направление наискорейшего роста функции в этой точке.
Градиент равен нулю когда все его компоненты равны нулю.
Градиент является расширением понятия производной на многомерный случай. Для случая одной переменной градиент просто заменяется на производную функции.
3. Необходимое условие локального безусловного экстремума во внутренних точках
Если
дифференцируемая
функция
имеет локальный экстремум во внутренней
(не бесконечной) точке
,
то ее градиент в этой точке равен нулю.
Условие является необходимым, но не достаточны. Возможны случаи, когда во внутренней точке градиент равен нулю, но у функции там не будет ни минимума, ни максимума.
Пример.
.
.
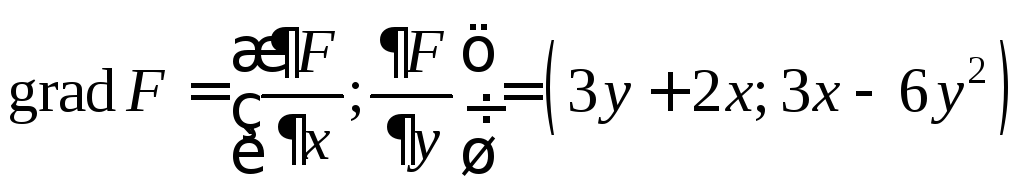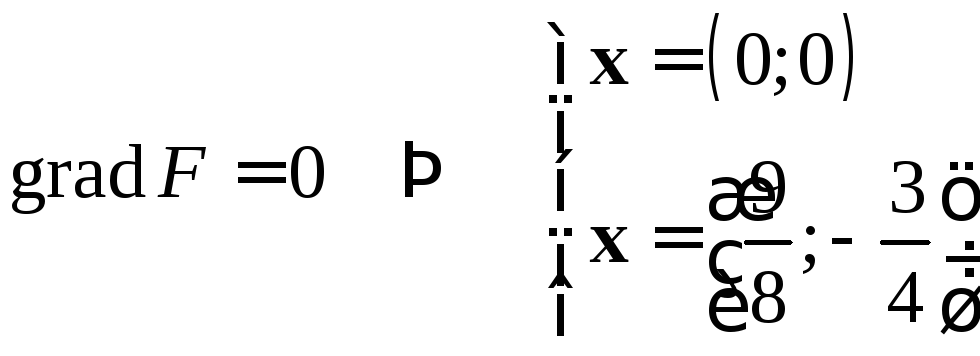
Таким образом, внутри у функции может быть локальный максимум или минимум только в двух точках. Более подробный анализ показывает, что первая точка не является точкой экстремума. Вторая точка – точка локального минимума.
4. Способы определения условного экстремума
Пусть требуется решить задачу на отыскание условного экстремума:
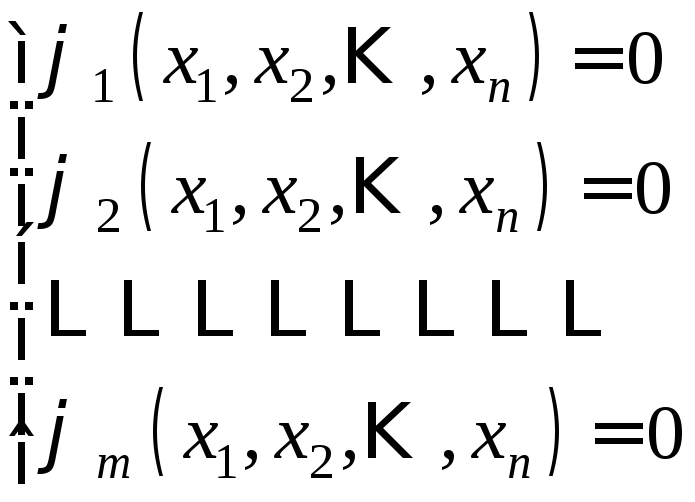(1)
Существуют два подхода к решению.
4.1. Выражение одной переменной через другие.
Можно выразить из условий (1) некоторые переменные через другие и подставить в функцию. Получим задачу на безусловный экстремум.
Достоинства подхода:
снижается число переменных;
снижается число уравнений;
подход интуитивно понятен.
Недостатки:
навязывается неравнозначность переменных (основные и зависимые);
после исключения сложно проанализировать влияние условий;
очень часто не удается явно выразить одну переменную через другие.
Последний недостаток оказывается критичным и непреодолимым при сложных зависимостях.
4.2. Метод множителей Лагранжа.
Для каждого
ограничения
вводится неизвестный множитель
.
После этого ищется безусловный экстремум
для функции Лагранжа:
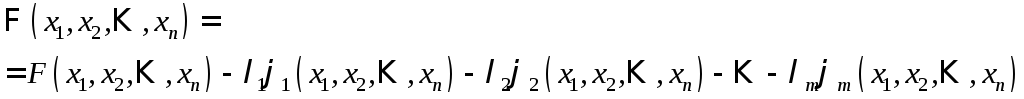
То
есть записываются
условий:
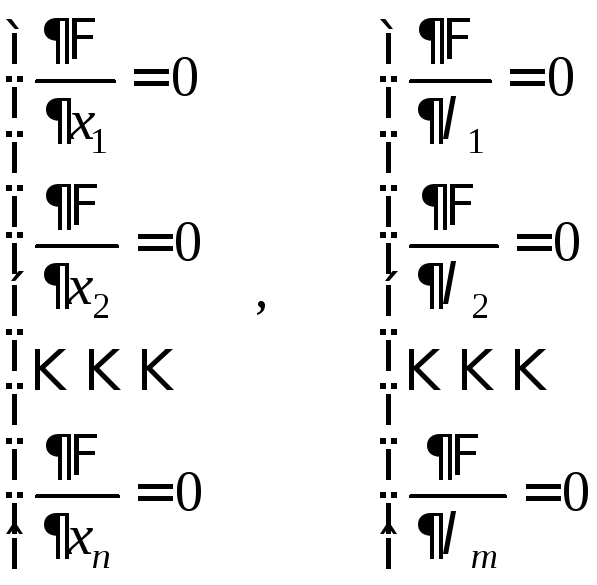
второй столбик условий, очевидно, является системой условий (1).
Недостатки подхода:
подход интуитивно не очевидный;
увеличивается количество неизвестных и количество уравнений;
сложные зависимости остаются в системе.
Достоинства:
всегда удается записать всю систему уравнений до того, как приходится выражать одну переменную через другие, следовательно, такой подход универсален;
множители Лагранжа имеют четкий смысл и позволяют проанализировать влияние ограничений.
Смысл множителей Лагранжа. Множитель Лагранжа, определенный для ограничения, показывает относительное изменение оптимального значения целевой функции при изменении правой части ограничения. То есть, если правая часть какого-либо из ограничений (1) изменится на некоторое значение, то и оптимальное значение функции тоже изменится. Отношение изменения функции к малому изменению ограничения равно множителю Лагранжа.
Кроме этого,
множителя Лагранжа продолжают играть
важную роль для задач нелинейного
программирования, когда вместо ограничений
равенствами (1) присутствуют ограничения
соответствующими неравенствами (
вместо
).
Тогда ненулевой множитель Лагранжа
означает выполнение в оптимальном
случае соответствующего ограничения
как равенства и имеет такой же смысл
как для равенств. Нулевой множитель
Лагранжа говорит о том, что в оптимальном
случае соответствующее ограничение
выполнено как строгое неравенство.
4.3. В качестве третьего подхода можно рекомендовать комбинировать оба способа. Выразить те переменные, которые легко выражаются через другие. Подставить всюду, тем самым, сократив число переменных и ограничений. Далее использовать способ Лагранжа.