
Ситникова Математика Ч. 1 для менедж
..pdf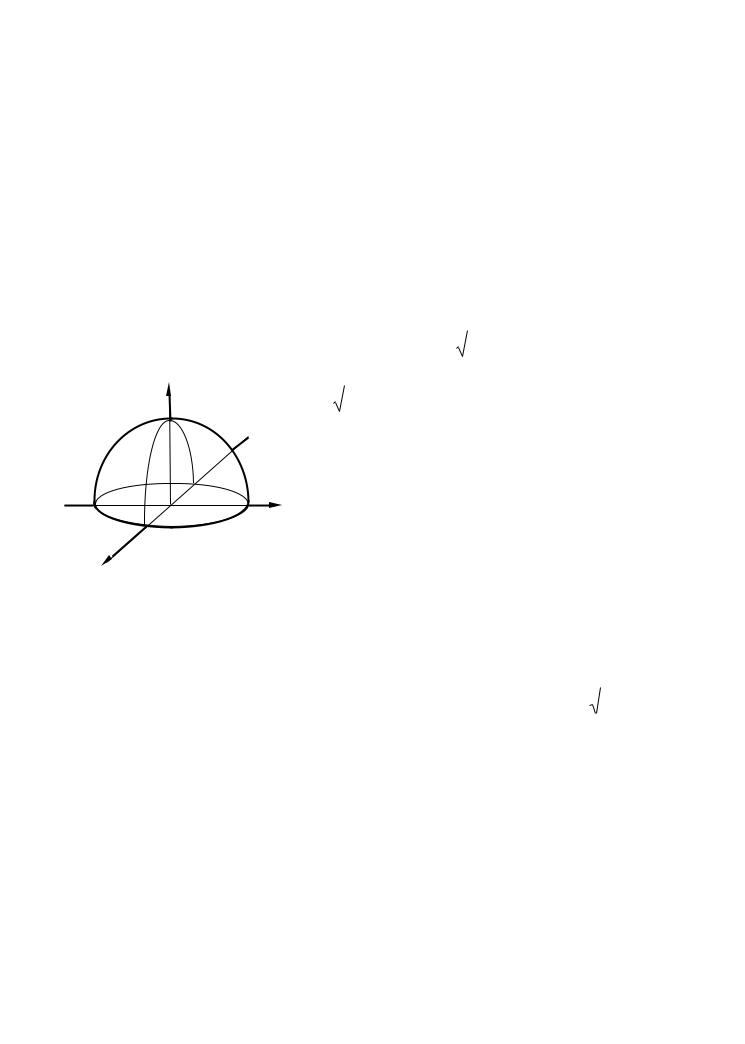
|
|
|
|
|
|
71 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
РАЗДЕЛV |
ΙΙ.ФУНЕСКОКЦИИ |
|
ЛЬКИХПЕРЕМЕННЫХ |
|
|
|
|
|
|
|
|
|||||||||
Понятиефункциидвухпеременных |
|
|
|
|
|
|
|
|
(x; y). |
|
|
|
|
|||||||
|
Пусть D |
это упоряд |
|
|
|
|
парчисел |
|
|
|
|
|||||||||
|
Соответствие f, |
каждойпаречисел |
|
|
|
|
(x; y) D соподноиставляет |
|||||||||||||
одействительное |
z = f |
y). |
z ,называется функциейдвухпеременных |
|
и |
|||||||||||||||
записываетсявиде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Приэтом |
и y называются независимымипеременными |
|
|
|
|
|
(аргументами), |
||||||||||||
а z – зависипеременной |
|
(функцией). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Множество D = D( f |
называется |
областьюопределения |
|
|
функции. |
||||||||||||||
Множествозначений,принимаемых |
|
|
|
z вобластиопределения,называется |
|
|
|
|
||||||||||||
областьюзначений |
|
этойфункцииобозначается |
|
|
E(f) или E. |
|
|
|
|
|||||||||||
. |
Найтиобластьопределенияфункции |
|
|
|
|
z = |
4 − x2 − y2 |
. |
|
|
|
|
||||||||
|
|
|
z |
|
Решение. |
|
Функциядвухпеременных |
|
|
|
|
|||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 − x2 − y2 ≥ 0. |
||||
|
|
|
множество пар (x; y) |
таких,что |
||||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
Записывают: |
|
D( f ) = {(x; y) |
|
|
4 − x2 − y 2 ≥ 0}. |
||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
Геометрическиобластьопределения |
|
|
|
|
|
|
|
Oxy, |
|||||||
|
|
|
O |
2 y |
представнекоторуючастьлоскостияет |
|
|
|
|
|
|
|
||||||||
|
|
2 |
изображающуюнеравенство |
|
|
4 − x2 − y2 ≥ 0.В |
||||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
x |
Рисунок 23 |
|
ирадиусом |
R=2. |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
являетсянекповето, редставляющаяхнсобоймножествостьвсехточек |
|
Графифункцииом |
|
двухпеременных |
||||||||||||||||
|
|
|
|
(x; y; z), |
|
z = f (x; y) называется |
||||||||||||||
пространства |
Oxyz |
скоординатами |
|
где |
||||||||||||||||
аппликатой точки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
. |
|
На |
рисункеизображен23 фун |
|
|
|
|
|
|
|
|
|
|
|
|
z = |
|
4 − x2 − y2 |
, |
|
представляющийсобойполусферуцентромточке |
|
|
|
|
|
|
|
|
O(0;0;0) ирадиусом R=2. |
|||||||||||
Частныепроизвпервогопоряддныедвухп ацииременных |
z = f (x; y).Т |
|
|
|
x |
и y |
|
|
|
|
||||||||||
|
Пустьфункция |
|
как |
– |
независимые |
|||||||||||||||
переменные,тооднанихизменяться,адругаясохранятьсвое |
|
|
|
|
|
x приращение |
x ,сохпраняяи |
|||||||||||||
значение.Придадимпеременной |
|
|
|
|
|
|
||||||||||||||
этом |
|
.Тогда |
|
получитприращение,котороеназывают |
|
|
|
|
|
|
|
частным |
||||||||
|
|
|
по x иобозначают |
|
x z .Итак, |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
z = f (x + x; y) − f (x; y). |
|
|
|
|
|
|
|
|
|||||||
Аналогичнополучаем |
|
частноеприращение |
|
z по y: |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
z = f (x; y + y) − f (x; y). |
|
|
|
|
|
|
|
|
|||||||
|
Частная |
|
|
функции |
|
z = f (x; y) |
вточке |
|
M (x; y)по |
|||||||||||
переменной x |
следующимравенством: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
72
вслучае,если |
|
|
x |
существует. |
|
|
→0 |
x |
частнаяпроизводная |
||||
Аналогичнымобозначается |
||||||
попеременной |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На длянахожденияпро спзвользуютдных |
|
|
|
||
правила,чтоивслучаедифференфункоднойцирования |
|
|
|||||
переменной,приэтом |
|
zʹx ,полагают |
y постоянной,апринахождении |
||||
zʹy |
– . |
|
|
|
|
|
|
Пример. |
Найтичастныепроизводные |
|
|
z = 4x + e x2 − y + 3. |
|||
Решение. |
|
|
|
|
|
||
zʹ |
= |
x + ex2 −y |
+ 3)ʹ = x)ʹ + |
2 −y )ʹ |
+ (3)ʹ = 4 + ex2 −y (x2 − y)ʹ + 0 = |
||
x |
|
|
|
x |
x |
x |
x |
= 4 |
x2 −y (2x − 0) = 4 2x e |
y ; |
|
|
|||
zʹ |
= x + e x2 − y |
3) = + e x2 |
(−1) + 0 = −e x2 − y . |
||||
y |
|
|
|
|
|
|
|
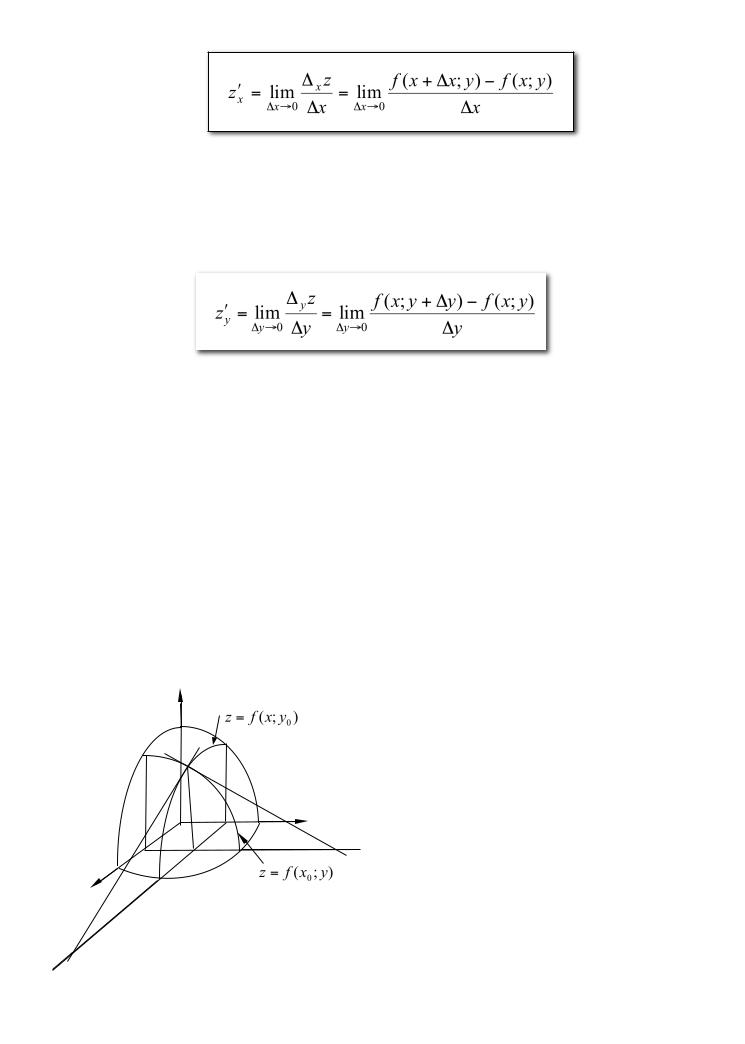
Геометрическийсмыпроизводныхтныхл
0
0
α |
Рис.24. |
кривой z = f (x |
0 ) |
Графифункомции |
|
z = f (x; y), |
|
некповерхностьто. ая |
|
|
|
производной |
zʹx |
вточке( |
x0;y0). |
Полагаем |
y = y0 ,тогдаграфик |
||
функции |
z = f (x; y ) естьлиния |
||
y = y .Исходяизгеометрического |
|
||
переменной,заключаем, |
|
что |
|
zʹx (x0 ; y0 ) = tgα ,где |
α – |
уголмежду |
|
осью Ox икасательной,проведенной
M x0 ; y0 ; f (x0 ; y0 )) (рис.24).
|
|
|
|
|
|
|
|
|
|
|
|
73 |
|
|
|
Аналогично, |
|
|
zʹy (x0 ; y0 ) = tgβ ,где |
β – уголмеждуосью |
Oy икасательной, |
||||||||||
проведеннойккривой |
|
|
|
z = f (x0 ; y) вточке |
M 0 (x0 ; y0 ; f (x0 ; y0 )) . |
|
|||||||||
Частныепроизввысшихпорядковдные |
zʹx |
и zʹy называются частнымипроизводными |
|
||||||||||||
|
|
Частныепроизводные |
|
||||||||||||
первогопорядка |
|
|
|
|
. Онитожеявляютсяфункциядвухпеременныхи |
|
x и y.Эти |
||||||||
функциимогутиметьчастныепроизв,котназордныеваются |
|
|
|
частными |
|||||||||||
произввтпорядкарогодными |
|
|
иопредслеобразомдуля:ютсящим |
|
|
||||||||||
|
|
zʹʹ |
= |
(z |
ʹ |
) |
ʹ |
; |
|
|
|
|
|
|
|
|
|
xx |
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
zʹʹ |
= |
(z |
ʹ |
) |
ʹ |
; |
|
|
|
|
|
|
|
|
|
xy |
|
|
|
x |
y |
|
|
|
|
|
|
|
|
|
|
zʹʹ |
= |
(z |
ʹ |
) |
ʹ |
; |
|
|
|
|
|
|
|
|
|
yx |
|
|
|
y |
x |
|
|
|
|
|
|
|
|
|
|
zʹʹ |
= |
(z |
ʹ |
) |
ʹ. |
|
|
|
|
|
|
||
|
|
yy |
|
|
|
y |
y |
|
|
|
|
|
|
|
|
|
|
Аналогичноопределяютсячастныетретьегоизводные..порядка. |
|
|
|
|
|
||||||||
Частныепроизводные |
|
вторилибовыслеегопо,взятыерядкакогопо |
|
|
|
||||||||||
различнымпеременным,называются |
|
|
смешаннымичастнымипроизводными |
|
. |
||||||||||
Например, |
zʹʹ . |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|
Приэтомследуучитывать,чтоеслипроизввысшегорядкадные |
|
|
|
|
|
||||||||
непрерывны,тосмешанныепроизводнодныег |
|
|
|
опорядка,отличающиесялишь |
|
||||||||||
порядкомдиффере,равмеждунсобойы.цированияТак,например, |
|
|
|
zʹʹ |
= zʹʹ . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xy |
yx |
Поэтомунапрактикедостнайоднуточноизакихпр .изводных |
|
|
|
|
|
||||||||||
Пример. |
Найтичастныепроизввторогопорядфункциидныеа |
|
|
|
|
|
|||||||||
y = x3 − 3xy2 + y3 + 2. |
|
|
|
|
|
||||||||||
Решение. |
Таккак |
|
zʹ |
= 3x 2 − 3y 2 |
и zʹ |
= −6xy + 3y 2 ,то |
|
|
|||||||
|
|
|
|
|
|
|
|
|
x |
|
y |
|
|
|
|
zʹʹ |
= (3x2 |
− 3y2 )ʹ = 6x, zʹʹ = (3x 2 − 3y 2 )ʹ |
= −6 y , |
|
|
||||||||||
xx |
|
|
|
|
|
|
|
x |
xy |
|
y |
|
|
|
|
zʹʹ |
= (−6xy + 3y 2 )ʹ = −6x + 6 y . |
|
|
|
|
|
|||||||||
yy |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
Экстремумфункциидвухпеременных( аксиминимумум |
|
|
|
м) |
|
||||||||||
|
|
δ-окрестностьюточки |
M 0 (x0 ; y0 ) |
называетсямножествовсехточек |
|
|
|||||||||
M (x; y) |
|
плоскос,координатыудовлетворяюторыхнеравенству |
|
|
|
|
|||||||||
|
|
|
|
|
|
||||||||||
|
(x − x0 )2 + (y − y0 )2 |
< δ .Сгеометточкизрения,ической |
|
δ-окрестностьточки |
|
||||||||||
M 0 (x0 ; y0 ) |
– этовсевнутренниеточкикругасцентром |
|
|
М0 ирадиусом δ. |
|
||||||||||
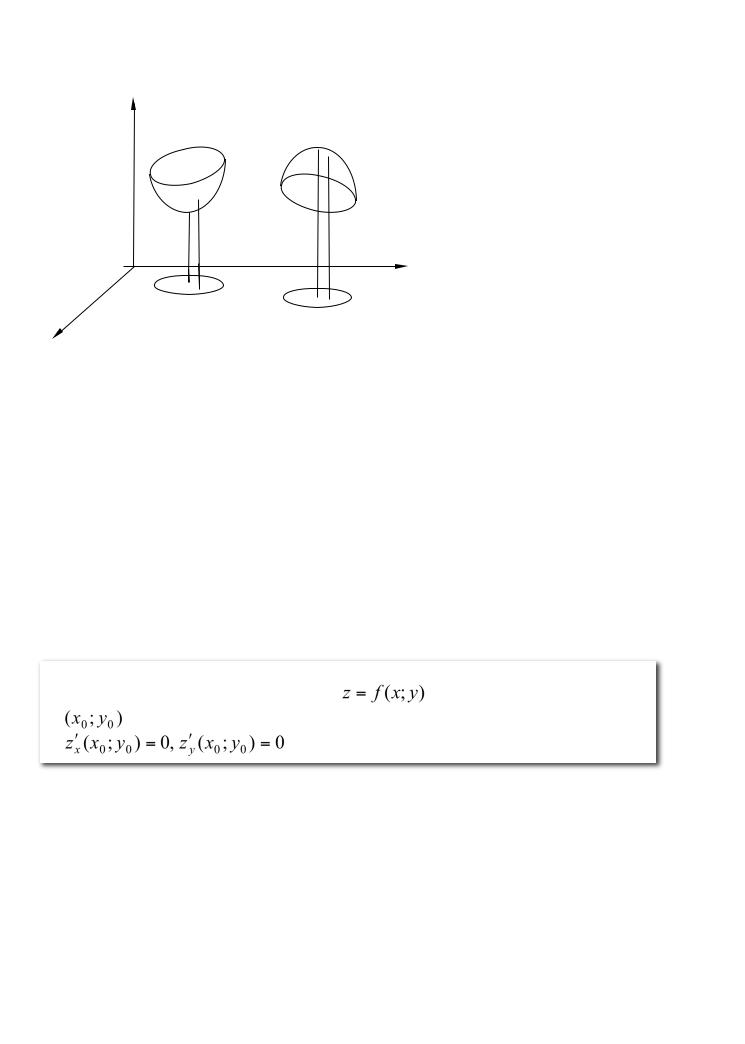
74
функция |
z = f |
z
•
•
f(x0;y0) f(x;y)
N1 • ••
x |
Рисунок 25 |
|
(x; y) определенавнекоторойобласти |
|
|
D,точка |
||
|
(x ; y ) D . |
|
|
||
• |
Точка |
(x0 ; y0 ) |
называется |
||
точкоймаксимума |
функции |
||||
• |
|||||
|
z = f (x; y),ес |
лисуществует |
|||
|
такая |
δ-окрестностьточки |
|||
|
(x0 ; y0 ),чтодлякаждойточки |
|
|||
y |
(x; y),отличнойточки |
(x ; y ) |
|||
,изэтойокрестности |
|
||||
N2 • • |
выполнянераветсянство |
|
|||
|
Точка |
(x0 ; y0 ) |
называется |
||
минимума |
функции |
z = f (x; y),е литакая |
δ-окрестность |
|
(x0 y0 ),чтодлякаждойточки |
(x; y |
отточки |
(x0 ; y0 ),изэтой |
|
выполняераветсянство |
|
f ( |
) > f (x0 ; y0 ). |
|
Нарисунке25: |
N2 – точкамаксимумафункции |
|
z = f (x; y). |
|
1 – минимума, |
|
|||
Значениефункцииточкемаксми(му)ниазываетсямума |
|
|
|
|
(минимумом) функции,или |
экстремумами функции. |
|||
Напрактикемаксимум минимумфункциинах дятмощью идостатсуществованиячноговийэкстремума.
Необхусловфункциидмое
д |
ифферефункцияцируемая |
имеетэксв очкеремум |
|
|
|
,то производнэторавныйчкенулю: е |
|
|
|
|
|
. |
|
|
|
|
|
||
|
Критическими точками функцииазываютсявнутренниеточки |
|||
определения,вкоторыхчастные |
|
ервпоравныгоядка |
||
лхотябыиоднаизчастныхпроизводныхнесуществует. |
|
|
||
|
Однаконелюбаякритичеточкабудетэксткаяфункцииремумом. |
O(0;0) для |
||
,подтверждающимэтотфактможетслужитьточка |
||||
|
z = xy, |
котораяявляекритичточкойся,ноявляетсяской |
|
|
функции. средикритичеточекуточкиэкстремумаких |
|
|
||
выявляютспомощью |
достаточного |
: |
|
|

|
|
|
75 |
|
|
|
|
|
|
Пустьвкритическойточке |
|
инекееокрестноститорой |
|
|
функция |
|
имнеетпрерывныечастныепроизводныедо |
|
|
второгопорядкавключительно.Вычислимточке |
|
|
значения |
|
|
|
|
.Обозначим |
|
|
|
|
. |
|
Тогда: 1) |
если |
тофункциявточке |
имеетэкс: ремум |
|
мак,еслиимум |
А<0 ;минимум,если |
A>0; если2) |
тофункцияв |
|
точке |
экстремуманеимеет. |
|
|
|
Вслучае |
=0эксвтремумочке |
|
можетбыть,аможетнебы. ь |
|
Необходимодополнительноеисследование. |
|
|
|
|
|
|
|
|
|
Плнахожденияэкстремумовфункции: |
|
z = f (x; y); |
|
|
|
||||
1) найтикритическиеточкифункции |
|
|
|
|
|||||
2) найтизначениеопред лителя |
|
длякаждойизкритическихточек; |
|
|
|
||||
3) всоответствиидостатуслэкстрчнымвиемсдвыводлатьмуманаличии |
|
|
|
|
|
||||
внейэкстремумаинайтиегозначение. |
|
|
z = 3xy − x3 + y3 . |
|
|
||||
Пример. |
Найтиэкстремумфункции |
|
|
|
|||||
Решение. |
1) |
zʹx = 3y − 3x2 ; |
zʹy = 3x + 3y 2 .Точки,вкоторыхчастные |
|
|
||||
произвнесущеотсутствуют, дные. |
|
|
|
|
|
||||
|
Найдемточки,вкоторыхониравнынулю,решаясистемууравнений: |
|
|
|
|
|
|||
3y − 3x 2 |
= 0 . |
|
|
|
|
|
|
||
3x + 3y 2 |
= 0 |
|
|
|
|
|
|
||
|
Получаемследующието |
чки: |
M1 (0;0), M 2 (−1;1) . |
|
|
|
|||
|
zʹʹ = −6x, zʹʹ = 3, |
zʹʹ = 6 y . |
|||||||
2)Находимчастныепроизввторогопорядка:дные |
|
|
|||||||
|
|
|
|
|
|
|
xx |
xy |
yy |
|
Вточке |
M1 (0;0) имеем: |
A=0, B=3, C=0, тогда |
= AC − B 2 |
= 0 − 32 |
= −9,т.е. |
|||
|
< 0. |
|
M 2 (−1;1) имеем: |
A=6, B=3, C=6, тогда |
= AC − B 2 = 6 6 − 32 = 27, |
||||
|
Вточке |
||||||||
т.е. |
> 0. |
M1 (0;0) экстремуманет. |
|
|
|
|
|||
3)Вточке |
|
|
|
|
|
||||
|
M 2 (−1;1) – точкаминимума( |
|
A=6>0), |
|
|
|
|||
|
zmin |
= z(−1;1) = 3 (−1) 1− (−1)3 +13 = −1. |
|
|
|
||||
Условныйэкстремумфункциидвухпеременных |
|
|
|
|
|
||||
|
Инпрактикеогдавозадникаетхождечаэкстремумафуниякции |
|
|
|
|
||||
двухпеременных |
x и y |
вслучае,когдаэтип ременныенеявляются |
|
|
|
||||

|
|
|
|
76 |
|
|
|
|
независимымидруготдруга.Соотмеждуниопшениемисывается |
|
|
|
|
|
|
||
уравнением ϕ(x; y) = 0,котороеназывается |
|
уравнениемсвязи |
.Такаязадача |
|||||
нахождеэкстремумафуниякции |
|
|
z = f (x; y) |
приусловии,что |
x и y |
|||
удовлетуравнениюс язиоряют |
|
|
ϕ(x; y) = 0 |
иноситназадачивание |
|
|||
нахожденияусловногоэкстр |
|
емума. |
|
|
|
|
|
|
Способрешенияэтойзадачизависитоттого,явлураяетсяисвнениези |
|
x или y. |
|
|
||||
разрешимымотноднойсительноизпеременных |
|
|
|
|
||||
1) Еслиуравнение |
ϕ(x; y) = 0 разрешимоотн днсительноизпеременныхй |
|
|
x |
||||
или y,тогдаизур связивыражаютнения |
|
|
однупеременнуючерездругуюи |
|
||||
подставляютнайденноевыражениефункцию |
|
|
|
z = f (x; y).Врезультате |
||||
получаютфункцию |
z |
однойпеременной |
x |
или y |
иисследуютеена |
|||
экстремум. |
ϕ(x; y) = 0 неразрешимоотн днсительной |
|
|
|
||||
2) Еслиуравнение |
|
зпеременных |
||||||
x или y,тогдасоставляюттакназываемую |
|
|
функциюЛагранжа |
: |
||||
F(x; y; λ) = f (x; y) + λ ϕ(x; y),где |
λ |
– вспомножительогательный, |
|
|||||
исследуютеенаэкстремумкакфункциюп ременных. |
|
|
z = 2x − y ,ес ли x2 + y2 |
|
||||
Пример. |
Найтиусловныйэкстремумфункции |
|
|
= 4. |
||||
Урасвязинение |
|
x2 + y2 = 4 |
неможетбытьразрешеоднозначно |
|
|
|||
относительнопеременной |
|
x |
|
или |
y.Преобразуемего: |
|
||
x2 + y2 = 4 x2 + y2 − 4 = 0. |
|
|
|
|
|
|||
СоставимфункциюЛагранжа: |
F(x; y;λ) = 2x − y + λ (x2 + y2 − 4). |
|||||||
Найдемчастныепроизводные |
|
первогопорядфункации |
|
F (x; y; λ): |
||||
Fxʹ = 2 + 2λx , Fyʹ = −1 + 2λy, Fλʹ = x2 + y2 − 4.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 + 2λx = 0 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Решаясистемууравнений |
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 + 2λy = 0 |
,находимкритическиеточки |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+ y |
2 |
− |
4 = 0 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
4 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
M |
|
|
|
|
|
; |
|
|
; |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1 |
|
− |
|
|
|
|
|
|
|
|
|
|
|
, M |
2 |
|
|
|
|
|
;− |
|
|
|
|
;− |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
5 |
|
|
5 |
|
4 |
|
|
|
|
5 |
|
|
5 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
Длякаждойиз |
|
|
|
|
|
критическихточексо |
|
|
|
|
|
|
|
|
|
ставляемопределитель |
: |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
ϕ |
ʹ ( x ; y |
0 |
;λ ) |
|
ϕʹ ( x ; y |
0 |
;λ ) |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
0 |
|
|
|
0 |
|
|
|
|
y |
0 |
0 |
|
( x |
|
; y |
|
|
|||||||||
|
|
|
|
= − |
ϕ |
ʹ |
( x ; y |
0 |
;λ ) |
|
F |
ʹʹ |
( x ; y |
0 |
;λ ) |
|
F ʹʹ |
( x ; y |
0 |
;λ ) |
,где |
0 |
0 |
;λ ) – |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
0 |
|
|
0 |
|
|
|
xx |
|
0 |
|
|
|
0 |
|
|
|
|
xy |
0 |
0 |
|
|
|
0 |
||||||||||||||
|
|
|
|
|
|
|
|
|
ϕ |
ʹ |
(x ; y |
0 |
;λ ) |
|
F |
ʹʹ |
(x ; y |
0 |
;λ ) |
|
F ʹʹ |
( x ; y |
0 |
;λ ) |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
0 |
|
|
0 |
|
|
|
xy |
|
0 |
|
|
|
0 |
|
|
|
|
yy |
0 |
0 |
|
|
|
|
|
|
||||||||||||
координатыкритическойточки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
Сначаланаходимчастныепроизвпервогопорядфундныекации |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
ϕ(x; y) = x2 + y2 − 4 ичастныепроизввторогопорядфундныекации |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Лагранжа F(x; y;λ) = 2x − y + λ (x2 + y2 − 4): |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
ϕʹ |
|
= 2x; ϕʹ |
= 2 y; Fʹʹ |
= 2λ; Fʹʹ |
= 0; Fʹʹ |
|
= 2λ. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
xx |
|
|
|
|
|
|
|
|
|
|
xy |
|
|
|
yy |
|
|
|
|
|
|
|
|
|
|
|||||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
77 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
4 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
5 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
(M1) = − |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
0 |
|
|
= 8 |
|
|
|
>0, (M 2 ) = − |
|
|
|
|
|
|
|
|
|
5 |
|
|
0 |
|
= −8 |
|
< 0 |
|||||||||||||||||||||||||
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
− |
|
5 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
− |
4 |
|
|
|
|
0 |
|
|
|
|
− |
|
5 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Значит, |
|
z |
− |
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
= − |
|
|
|
|
– условныйминимум, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
5 |
|
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
4 |
|
|
2 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
z |
|
|
|
;− |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
– условныймаксимум. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
5 |
5 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Упражнение15 |
. |
|
|
|
|
|
|
|||||
|
15.Найти1 области |
|
|
|
пределенфункциизобразитяй |
1 |
|
|
|
|
|
ь |
полученное |
|||||||||||
множествокоординатнойплоскости:) |
|
|
|
|
|
|
|
|
z = |
|
;б) |
z = |
; |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
x + y |
|
|
|
|
|
||
в) |
z = ln(x + y) ;г) z = arcsin |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
15.2Постролинииуровняследтьфу:а)нкцющихй |
|
|
x2 |
|
|
|
|
|
|
|
|
z = xy : |
|
||||||||||
|
|
y − x2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
б) z = x + y ;в) |
z = |
x |
;г) z = |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
y |
|
|
|
x2 |
|
|
|
|
|
|
|
|
z = x3 + 3x2 y − y3 ; |
||||||
|
15.3Найтичастные. производныеотфункций:а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
б) |
z = |
x |
;в) |
z = x2 sin y ;г) |
z = x |
+ |
y |
;д) |
z = |
|
xy |
|
;е) |
z = arctg |
y |
; |
|
|||||||
|
|
|
|
|||||||||||||||||||||
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
x − y |
|
|
x |
|
||||
ж) |
z = xye2 x+3y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
||||||
|
15.4Найтичастные. произввторогопорядка:)дные |
|
|
|
|
|
|
|
|
|
|
|
|
|
z = |
|
; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1− 2y |
||||||||||
|
z = xey ;в) |
z = sin x cos y ;г) |
|
z = ln(x + exy ) ;д) |
z = x2 y . |
|
||||||||||||||||||
б) |
|
|
|
|
|
|||||||||||||||||||
|
15.5Найти. экстремумыфункции: |
|
|
|
|
|
|
|
а) |
z = x2 + y2 + xy − 4x − 5y ; |
|
|||||||||||||
б) z = y2 − x2 + xy − 2x − 6y ;в) |
|
z = y |
− y2 − x + 6y ;г) |
z = x2 y − y3 − x2 − 3y2 + 3; |
||||||||||||||||||||
д) z = ex 2 (x + y2 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
15.6Найтиусловные. экстремумыфункции: |
|
|
|
|
|
|
|
|
2x + 5y =100 ; |
|
|
|
|
||||||||||
а) |
z = xy2 при x + 2y = 4 ; б) |
|
|
z = |
|
при |
|
|
|
|
||||||||||||||
в) |
z = 2x + y при x2 + y2 = 5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
78 |
|
|
|
|
|
|
|
|
|
|
15.7Найтивыс. радиусоснованиятуцилиндранаибольшегообъема, |
|
|
|
|
|
|
|
|
|
|
|
|
еслиегоп поверхностьлнаяравна |
6π . |
|
|
|
|
|
|
|
|
|
|||
|
15.8Общиеиздержки. производствазаданыфу |
|
|
|
|
|
|
|
|
|
|
нкцией |
|
z = 0, 5x2 + 0, 4y2 + 0, 6xy + 700x + 600y + 2000 ,где |
х и у – количествотоваровА |
||||||||||||
В.Общееколичествопроизведенпродукциидолжбытьравно500ед. й |
|
|
|
|
|
|
|
|
|
|
|
||
СколькоедиництовараАВнужнопроизводить,чтобыиздержкинаих |
|
|
|
|
|
|
|
|
|
|
|
||
изготовлениебылиминимальными? |
|
|
|
|
|
|
|
|
|
|
|
||
|
Домашзадани№ ее |
|
|
|
15 |
|
|
||||||
|
1Найти. частныепроизводныефункций: |
|
|
|
|
|
|
|
|
|
y |
||
|
z = 2x2 − xy2 + 3x2 y − 2y3 + 3x − 4y +1;б) |
z = arcsin(xy) ;в) z = e− |
|||||||||||
а) |
x |
; |
|||||||||||
г) |
z = ln( + ) . |
|
|
z = x2 + y2 − xy + 9x − 6y + 20 ; |
|||||||||
|
2Найти. экстремумыфункций:а) |
|
|
||||||||||
б) z = xy2 − xy3 − xy (x > 0, y > 0) ;в) |
z = |
|
xy |
. |
|
|
|
|
|
|
|||
x |
|
|
|
|
|
|
|||||||
|
3Найти. условныеэкстремумыфункции: |
|
2 + y2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
1 |
|
|
|
||
а) |
z = x2 + y2 − xy + x + y при x + y + 3 = 0 ;б) |
z = |
+ |
при x + y = 2 . |
|||||||||
x |
|
||||||||||||
|
|
|
|
|
|
|
|
y |
|||||
Задомашнейанияконтрольнойработы№1
1Провести. полноеисследованиепостр
1 |
y = |
1 |
|
x3 |
− 2x2 − 2x + 3 |
||||||
|
|
||||||||||
3 |
|
|
|
|
|
|
|||||
|
|
|
3 |
|
|
||||||
|
y = x2 + |
|
|
||||||||
|
|
x |
|||||||||
|
|
|
2 |
|
|
||||||
3 |
y = |
x3 |
− 3x2 − 2x + 4 |
||||||||
|
|||||||||||
3 |
|
|
|
|
|
|
|||||
|
|
|
3 |
|
|||||||
|
y = 2x + |
|
|||||||||
|
|
|
x − 2 |
||||||||
|
|
|
|
|
|
|
|
||||
5y = x3 − x2 −3x + 5 y = −x2 + 3x
7 y = 2x3 − |
1 |
|
x2 − 3x + 6 |
||||||||||||||
2 |
|||||||||||||||||
|
y = 4x2 + |
8 |
|
|
|
|
|
|
|||||||||
|
|
x |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
9 |
y = − |
1 |
|
x3 |
+ |
|
3 |
x2 + 2x − 8 |
|||||||||
|
|
|
|||||||||||||||
3 |
|
|
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
||||||||||||
|
y = 5x − |
|
|
2 |
|
|
|
|
|||||||||
|
|
x + 3 |
|||||||||||||||
|
|
2 |
|
|
|||||||||||||
11 |
y = − |
x3 |
|
|
+ 3x2 + 3x − 5 |
||||||||||||
|
|||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
3 |
|
|
|
|||||||||
|
y = −2x + |
|
|
|
|||||||||||||
|
|
|
x − 3 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
13 |
y = −x3 + |
1 |
x2 + 2x − 4 |
||||||||||||||
|
|||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
y = 2x + |
|
6 |
|
|
|
|
||||||||||
|
x −1 |
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||
y = −2x3 + x2 + 5x −3
15 |
6 |
|
y = −3x2 + |
||
x |
||
|
y = |
1 |
|
x3 |
+ 2x2 − 3x − 5 |
|||||
3 |
|||||||||
17 |
|
|
|
3 |
|
|
|||
|
|
|
|
|
|
|
|||
y = 5x − |
|
|
|
|
|||||
|
x + 2 |
||||||||
|
2 |
|
|
||||||
y = |
x3 |
|
− x2 − 3x + 4 |
||||||
3 |
|
||||||||
19 |
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|||
y = −5x + |
|
|
|||||||
x −1 |
|||||||||
|
|
|
|
|
|
||||
79
Приложения
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
оитьграфифун. кций |
||||||||||||||
2 |
y = −2x3 |
+ 2x2 + 3x − 5 |
|||||||||||||||||||||||||||||
y = 3x − |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
x + 2 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
4 |
y = |
1 |
|
|
|
x3 |
+ x2 − 4x + 6 |
||||||||||||||||||||||||
3 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||
|
y = −2x2 |
+ |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
x |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
6 |
y = |
2 |
|
|
x3 |
− |
1 |
|
x2 − 4x + 5 |
||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
y = −3x + |
|
2 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
x + 3 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
8 |
y = x3 + x2 −5x −3 |
||||||||||||||||||||||||||||||
y = −4x − |
|
8 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
x −1 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
10 |
y = 2x3 + x2 − 5x + 2 |
||||||||||||||||||||||||||||||
y = −5x2 |
+ |
10 |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
x |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
12 |
y = − |
1 |
|
x3 |
|
|
+ x2 + 2x + 3 |
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
y = x2 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
x |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||
14 |
y = − |
x3 |
|
|
+ x2 + 3x − 2 |
||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
y = 3x − |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
x +1 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
16 |
y = −x3 + x2 + 4x + 5 |
||||||||||||||||||||||||||||||
y = 2x + |
|
3 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
x − 2 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
18 |
y = −2x3 |
+ |
1 |
x2 + 4x − 3 |
|||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
y = 4x2 |
+ |
42 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
x |
|
|||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
y = |
|
x3 |
− x2 − 5x + 4 |
|||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
20 |
|
|
|
3 |
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|||||||||||
y = 5x2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
+ |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
x |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
80
21 |
y = x3 + 2x2 − 2x + 5 |
22 |
y = −x3 + 2x2 + 3x − 4 |
||||||||||||||||||||||||||||||||||
y = 2x2 − |
3 |
|
|
|
|
y = −x + |
|
|
|
|
3 |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
x |
|
x − 3 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
23 |
y = 2x3 − x2 − 4x + 3 |
24 |
y = x3 − |
1 |
|
x2 − 4x + 5 |
|||||||||||||||||||||||||||||||
3 |
|
|
|
|
|
2 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
y = x − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|||||||||||||
|
x + 3 |
|
y = −2x |
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||||||||||||||
25 |
y = − |
1 |
|
x3 |
− 2x2 + 4x − 5 |
26 |
y = 2x3 + |
1 |
|
x2 − 3x − 3 |
|||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
y = −4x2 + |
8 |
|
|
|
y = 2x + |
6 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
x −1 |
||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
x |
|
|
|
1 |
|
|
|||||||||||||||||||||
27 |
y = − |
x3 |
+ 2x2 + 4x + 3 |
28 |
y = − |
x3 − x2 + 5x + 2 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||
|
y = 3x2 + |
|
|
|
|
|
|
y = −4x + |
|
|
|
|
|||||||||||||||||||||||||
|
x |
|
x − 3 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
29 |
y = |
2 |
x3 + x2 − 5x + 3 |
30 |
y = − |
2 |
x3 + |
3 |
x2 + 4x − 5 |
||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||
|
y = 4x − |
|
3 |
|
|
|
|
y = −5x2 − |
|
3 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||||||||||||||||||||||||
|
x − 2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
