
Ситникова Математика Ч. 1 для менедж
..pdf
|
|
|
|
|
|
|
|
|
|
61 |
|
|
|
|
|
|
|
|
9) y = |
|
|
|
|
|
; 10) y = sin2 x3 ; 11) y = (cos3x) |
; 12) y = 2xarctgx ; |
|
|
|
||||||||
13) cos(x − y) − 2x3 + 4y4 = 0 ; 14) xey + yex = xy . |
|
|
|
|
|
|
||||||||||||
РАЗДЕЛV |
|
Ι.ПРИЛОЖЕНИЯПРОИЗВОДНЫХ |
|
|
|
|
|
|
|
|
||||||||
ПравилоЛопиталя |
y = f (x) и |
y = ϕ(x) дифференцируемывокрестности |
|
|
||||||||||||||
|
|
|
Пустьфункции |
|
|
|||||||||||||
точки |
|
x0 |
иобращаютсявнульвэто:йчке |
|
|
|
|
f (x0 ) = ϕ(x0 ) = 0 |
или |
|||||||||
lim |
f (x) = lim ϕ(x) = ∞.Тогда, |
lim |
f (x) |
|
= lim |
f ʹ(x) |
,если |
lim |
f ʹ(x) |
|
||||||||
ϕ(x) |
|
ϕʹ(x) |
||||||||||||||||
x→x0 |
|
|
|
|
|
x→x0 |
|
x→x0 |
x→x0 |
ϕ (x) |
x→x0 |
|||||||
|
|
|
|
|
|
|
|
ʹ |
|
|
||||||||
существует. |
|
|
|
|
|
|
|
|
|
|
||||||||
|
0 |
Этоутверлевжосноведениеметодаитраскрытияне |
|
|
|
|
|
определенностей |
||||||||||
|
и |
∞ |
|
спомощьюпроизводной. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
0 |
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример. |
Вычислить lim |
x2 −2x |
. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x→2 |
x2 −3x + 2 |
(x2 |
− 2x)ʹ |
|
|
|
|
|
|
||||||
Решение. |
lim |
x2 − 2x |
= |
|
0 |
= lim |
= lim |
2x − 2 |
= |
4 − 2 |
= 2. |
||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||
|
x→2 |
x2 − 3x + 2 |
|
|
0 |
x→2 (x2 − 3x + 2)ʹ |
x→2 |
2x − 3 |
|
4 |
− 3 |
|
|||||
Монотонностьвозрастание( или |
убывание)функции |
|
(a;b),есдляи |
||||
|
Функция y = f (x) называется возрастающей наинтервале |
||||||
любыхзначений |
x1, x2 (a; b) таких,что |
x1 < x2 , |
f (x1 ) < f (x2 ) . |
(a;b),есдляи |
|||
|
Функция |
y = f (x) |
называется |
убывающей |
наинтервале |
||
любыхзначений |
x1, x2 (a; b) таких,что |
x1 < x2 , |
f ( x1) > f ( x2 ) . |
|
|
||
|
Однакоспомэтогопределещьюпрактическиневозможнонайтиия |
|
|
|
|
||
промежуткивозрастаубыванияфу.Длрешениякцииэтойзадачи |
|
|
|
|
|
||
существуетболееудобныйметод |
|
,теоретичеосновукот рогокуютавляют |
|
|
|||
необходимыедостатусл чныевия |
|
возрастаубыванияи фу. кции |
|
|
|||
Необходусловия. мые |
|
|
|
|
|
||
|
Еслидифференцирунаинтервалемая |
|
функция |
|
|
||
|
возрастает,то |
длявсех |
|
. |
|
|
|
|
|
|
|
|
|
|
|
Еслидифферен |
цируемаянаинтервале |
функция |
убывает,то |
длявсех |
. |
|
|
|
62
Достаточныеусловия.
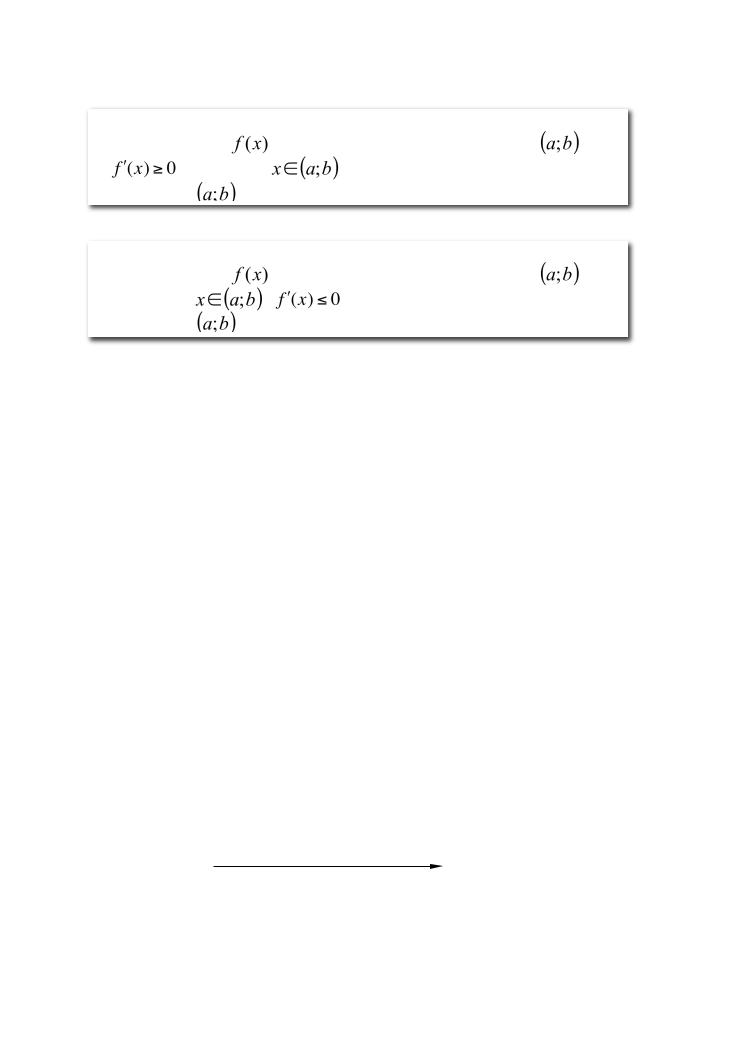
Еслифункция |
дифференцируеманаинтервале |
и |
длявсех |
,тоэтафункциявозрастаетна |
|
интервале |
. |
|
|
Еслифункция |
|
|
|
дифференцируеманаинтервале |
|
|
и |
|
|||
|
длявсех |
|
|
|
|
|
,тоэтафу |
убываетна |
|
|
|
|
|
интервале |
|
. |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||||
|
Рассмтепозволяюттренныеремыдостаточнопростоисследовать |
|
|
|
|
|
||||||
функцию намонотонность,аименно: |
|
|
|
|
|
|
|
|||||
|
1) находим D( f ); |
|
|
|
|
|
|
|
||||
|
2) находпроизводнуюм |
|
f ʹ(x) ; |
|
|
|
|
|||||
|
3) решаемнеравенства: |
|
|
f ʹ(x) ≥ 0 и f ʹ( |
0.Промежутки,являющ еся |
|||||||
|
решпенеравенстварвогонием,будутпромежутквозрастаминя |
|
|
|
|
|
||||||
|
функции,авторого |
|
|
|
– промежуткамиубывания. |
|
|
|
|
|||
Пример. |
Исследоватьфункцию |
|
|
y = x2 − 5x + 4 на иубывание. |
|
|
|
|||||
Решение. |
1) |
D( f ) = (− ∞; ∞); |
|
|
|
|
|
|||||
2) f ʹ(x) = 2x − 5 ; |
|
|
|
|
|
|
|
|
|
|||
3) 2x − 5 > 0 при x (2,5; ∞); 2x − 5 < 0 при x |
∞;2,5). |
|
|
|
||||||||
Ответ:функц |
ия |
y |
= x |
2 |
− 5x + 4 |
возрастаетна |
( |
∞ |
) иубываетна |
|||
|
|
|
|
|
|
2,5; |
|
|
||||
интервале (− ∞;2,5).
Экстремумыфункциимаксминимум( ) |
|
|
|
|
|
|||
|
Длятогочтдатьопределебыэкстремумовфу,введемнпонятиекции |
|
|
|
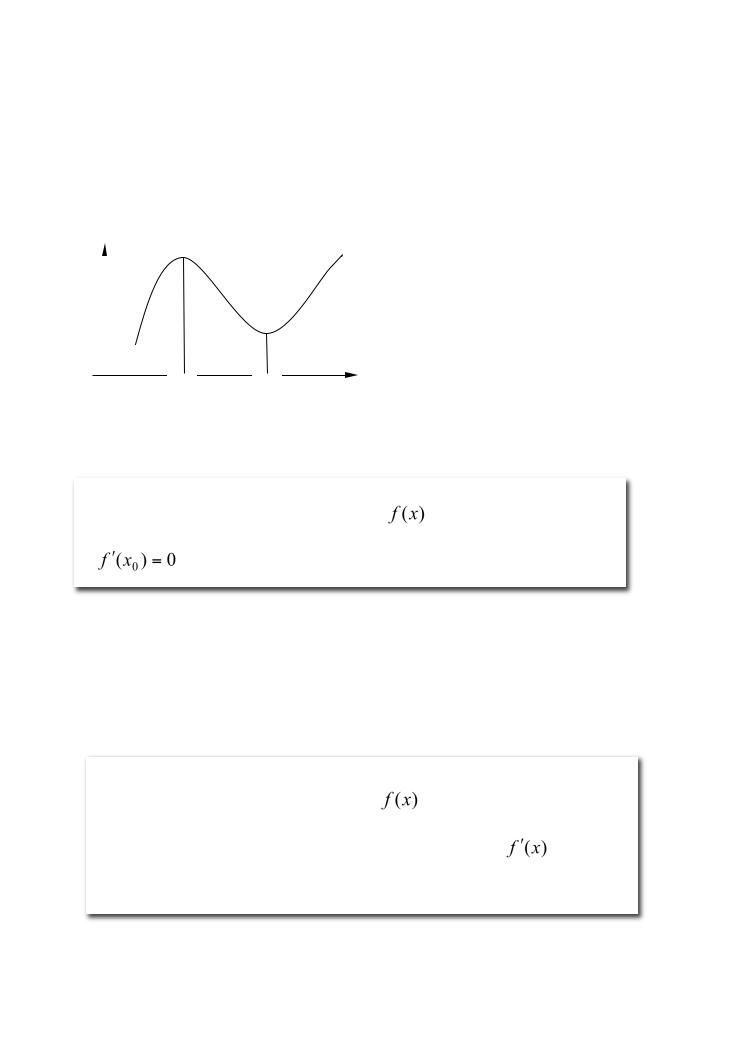
0 − δ ; x0 + δ ) называется δ- |
|||
δ-окрестноститочки |
x0.Ин |
тервалвида |
|
|||||
окрестностьюточки |
x0. Длявсех |
|
x (x0 − δ ; |
|
+ δ ) выполнянераветсянство |
|||
|
x − x0 |
|
< δ . |
( |
• |
) |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||
|
|
|
|
x0-δ |
x0 |
x0+δ |
x |
|
Рис.14
|
|
|
|
|
|
|
|
63 |
|
|
|
|
|
|
|
|
Точка |
x0 |
называется |
максимума |
|
функции |
y = f (x),если |
||||||
существуеттакая |
|
δ-окрестнточкисть |
|
x0,чтодлявсех |
|
x ≠ x0 |
изэтой |
|||||||
окрествыполняеравостиетсянство |
|
|
f (x) < f (x0 ). |
|
y = f (x),если |
|||||||||
|
|
Точка |
x1 |
называется |
минимума |
|
функции |
|||||||
существуеттакая |
|
δ-окрестностьточки |
|
x1,чтодлявсех |
|
x ≠ x1 |
изэтой |
|||||||
окрествыполняеравостиетсянство |
|
|
f (x) > f (x1 ) (рис.15). |
|
|
|
||||||||
|
|
Точ имиифниуназываютсямнкцииума |
|
|
|
|
точкамиэкстремума |
|||||||
|
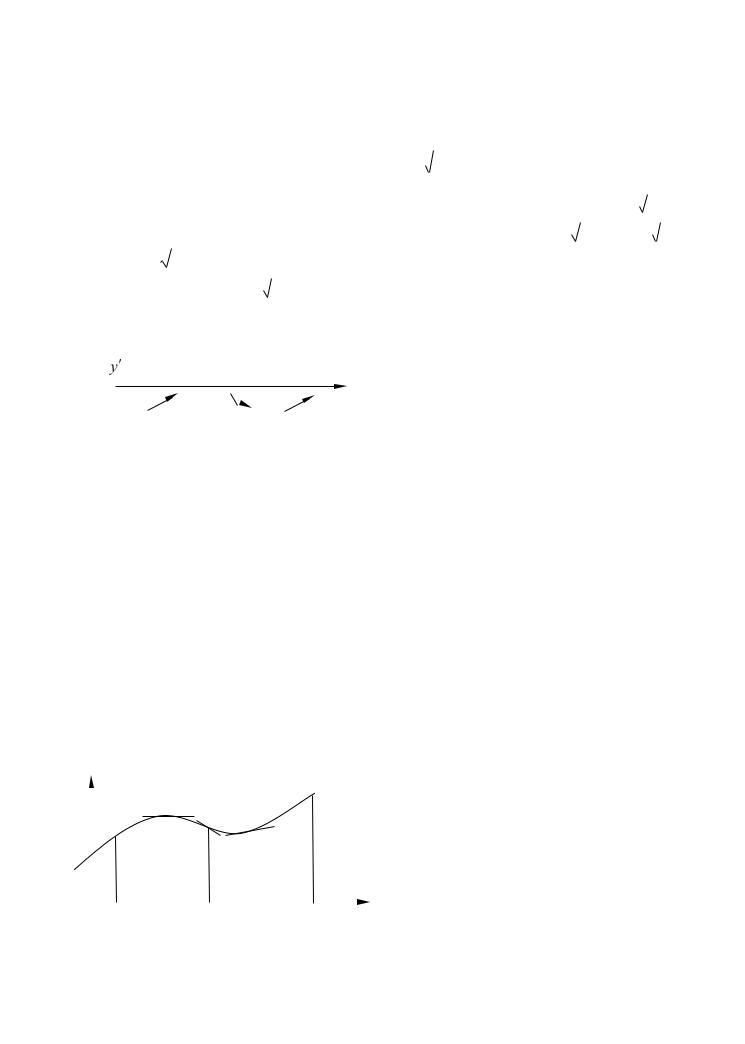
y |
|
|
|
y=f(x) |
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
минимумом. |
|
|
|
|
|
|
|
|
|
|
max |
|
|
|
|
Какивслуча |
есмонотонностью |
|||
|
|
|
|
|
|
|
|
функции,поопределениюэкстремумы |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
min |
|
|
найтипрактическиневозможно. |
|
|
|
||
|
|
|
|
|
|
( |
|
x экстремумоврешаютпомощью |
|
|
|
|||
|
|
|
|
|
x0-δ x0 |
x0+δ x1-δ x1 |
x1+δ |
|
|
|
||||
|
|
|
|
|
|
Рис.15 |
|
|
необходимдостатусл. очноговий |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Необхусловиэкстремумад. мое |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Еслидифференфункцируемая |
|
|
|
имеетэксв ремум |
|
|
|
|||||
|
|
точке |
x0,тоеепроизводэторавйчкенулю: ая |
|
|
|
|
|
|
|
||||
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Криточкамииескими |
функцииназываю |
тсявнутренниеточкиобласти |
|
|
||||||||
определения,вкоторыхпроизводная |
|
|
f ʹ(x) |
равнануилнесуществуетюи. |
|
|
||||||||
Однаконелюбаякритичеточкабудетэксткаяфункцииремумом.Примером, |
|
|
|
|
x=0 дляфункции |
|
y=x3. |
|||||||
подтверждающимэтотфактслужитьточка |
|
|
|
|
|
|||||||||
Поэтомусредикритичеточкиэкстремумакихфункциивыявляют |
|
|
|
|
|
|
|
|
||||||
помощью достаточногоусловия |
: |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Еслинепрерывнаяфункция |
|
|
|
дифференцируемав |
|
|
||||
|
|
|
|
некоторой δ-окрестностикрит |
|
ическойточки |
x0 |
ипри |
|
|
||||
|
|
|
|
перчнееходерслева( наз)правооизводная |
|
|
|
|
меняет |
|
|
|||
|
|
|
|
знаксплюсанаминус, то |
|
|
x0 естьточкамаксимума; |
|
|
|
||||
|
|
|
|
минусанаплюс,то |
x0 – точкa минимума. |
|
|
|
|
|||||
|
|
Планисследованфуннаэкцистремум: ия |
|
|
|
|
|
|
|
|
||||
1) |
|
указать D( f ); |
|
|
y = f (x); |
|
|
|
|
|||||
2) |
|
найтикритическиеточкифункции |
|
|
|
|
|
|
||||||
3) |
|
|
|
исследзнакпровать |
|
|
|
|
|
|
f ʹ(x) |
слеваиспроткаизваждой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
найденныхточек; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4) |
|
|
|
всоответстдостатуслоиичнымвиемэкс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
вычислизначенэтихь.я |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример. |
экстремумы |
|
|
|
|
|
= |
|
|
x 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|||
Решение. |
|
|
|
D( f ) |
(− ∞; |
Находим |
|
|
yʹ |
= |
1 |
− |
2 |
|
|
= |
1 |
|
|
x |
|
− 2 |
; |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 3 |
x |
|
|
3 x |
|
||||||||||
yʹ = |
, если |
|
|
− 2 = |
x = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
yʹ − не существует, |
3 |
|
= |
|
|
|
.Такимобразом, |
|
|
|
|
x=0 |
|
|
и |
|
x=8 – |
||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
критическиеточки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
– |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
y |
|
|
|
• |
• |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
0 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Рис.16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) x=0 – |
максимума, |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x=8 – точкаминимума, |
ymin |
( |
|
|
4 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Выпуклостьграфиперегибафун.Точк |
|
|
|
|
|
|
|
|
|
|
|
y = f (x) |
|
|
|
|
|
|
|
|
выпуклым |
||||||||||||||||||
|
|
|
|
дифференфункциируемой |
|
|
|
|
|
|
|
|
называется |
||||||||||||||||||||||||||
вниз |
(вогнутым) |
наинтервале |
|
|
|
),еслионрасположенвышелюбой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
касательной,провтоеденной |
|
|
|
чкеи |
|
|
|
|
|
|
y = f (x) |
|
|
|
|
|
|
|
|
выпуклым |
|||||||||||||||||||
|
|
|
|
дифференфункциируемой |
|
|
|
|
|
|
|
|
называется |
||||||||||||||||||||||||||
вверх |
наинтервале |
;b),еслирасположенлюбой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
проточкееденнойи .тервала |
|
|
|
|
|
|
|
|
|
|
y = f (x),вкоторойпроисходит |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
непрерывнойф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
y |
|
|
|
|
|
|
.M |
|
|
|
|
|
|
|
перегиба. |
|
|
|
|
|
|
|
|
|
|
|
y = f (x) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нарисункекривая17 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выпуклавверхнаинтервале |
|
|
|
|
|
|
|
|
|
|
|
|
|
(a;с), |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выпукланинтервалеиз |
|
|
|
|
|
|
|
|
|
|
|
|
|
(с;b), |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точка М (с; f (c))– точкаперегиба. |
|
|
|
|
|
|
|
||||||||||||||||
|
O |
|
|
a |
|
|
|
c |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Рис.1 7
Напракинтикеервалы
выпукловверхи находятсяпомощьютиследу: щей

|
Еслифункция |
вовсехточкахинтервала |
|
имеет |
||
|
отрицательнуювтоп оизводную,.. |
|
|
,то |
||
|
графикфуннаэтоминтервалециивыпуклыйвверх.Еслиже |
|
|
|
|
|
|
длявсех |
|
,тографик |
– выпуклыйвниз. |
||
|
Для нахожденточекперегграффунияиспользуютбакации |
|
|
|
||
достаточноеусловие |
их : |
|
|
|
|
|
|
|
|
|
|
|
|
|
Если |
приперчеточкуходерез |
|
x0,вкоторойонавна |
|
|
|
нуилинесущею,меняетсвойзнактвует,точкаграфика |
|
|
|
|
|
|
сабсциссой |
x0 являетсяточкойперегиба. |
|
|
|
|
|
Планисследованиявыпуклост |
играфифункации |
: |
|
||
1) указать D( f ); |
|
|
|
|
|
|
2) найтизначения |
x,прикоторых |
f ʹʹ(x нуилнесуществуетюи; |
||||
3)выбратьсрединихзначения,принадлежащиеобластиопределения;
4)исследоватьзнак f ʹʹ(x) слеваисправаотвыбранных.Всоответствии
сознаком |
f ʹʹ(x) выпромежуткиисатьвыпуклостивверхвниз; |
|
5) указатьточкиперегиба,опираянадостатусльихсущовиечное. ствования |
|
|
Пример. |
Исследоватьнавыпуклостьито |
чкиперегибаграфикфун ции |
y = x3 − 2x + 5. |
|
|
Решение. |
1) D( f ) = (−∞;+∞); |
|
2)yʹ = 3x2 − 2; yʹʹ = 6x yʹʹ = 0 при x = 0;
3)x = 0 D( f );
4)наинтервале |
(− ∞;0) – функциявыпуклавве |
рх; |
||||||
наинтервале |
(0;∞) – функцвыпуклавнр(.и18);язс |
|
||||||
|
|
|
|
– |
|
|
+ |
|
|
|
|
|
y |
|
• |
x |
|
|
|
|
|
|
0 |
|
||
|
|
|
|
|
Рис.18 |
|
|
|
5) |
y(0) |
= 0 |
3 |
− 2 0 + 5 |
= 5 |
; |
( )– точкаперегиба. |
|
|
|
|
0;5 |
|
||||
66
Асимптотыграфифункцииа
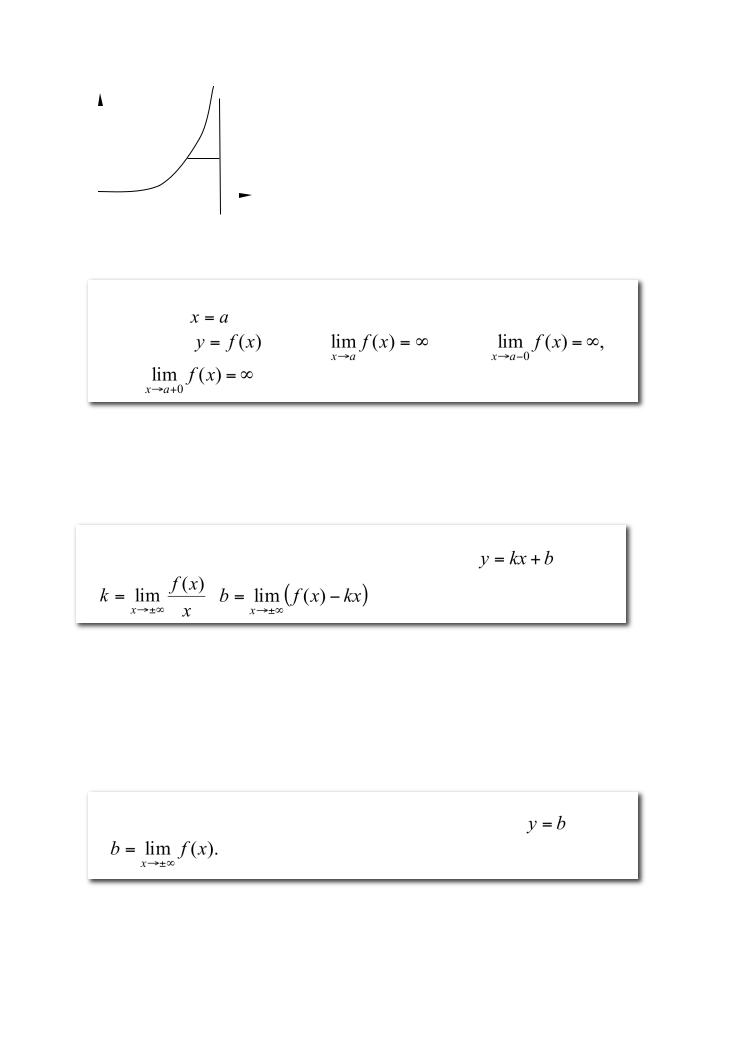
Асимптотой кривойназываетсяпрямая,к
y |
|
y=f(x) |
|
удаленияихотначалакоо,т.е.рдинатассотояние |
||
|
|
|||||
|
|
|
|
|||
|
|
|
|
|
||
|
|
M |
d |
|
точкикривойдоасимптотыстремитсякнулю |
|
|
|
|
|
d → 0 |
приудаленточквбесконечностьии |
|
|
|
|
|
|
|
|
O |
|
|
a |
x |
Асимптотыбываютверти,наклонныеальные |
|
|
|
|||||
|
|
|
|
|
||
|
|
Рис.19 |
|
|
игоризонтальные. |
|
Прямая |
является вертикальной асимптотойграфика |
|
функции |
,если |
,или |
или |
. |
|
|
|
|
. |
x = a |
y = f (x) имеетразрыввторогорода.Всилу |
этого, функцияэлемент,товертикальныернаяонаможет толв точкахехнопределена.
|
|
Уравнение наклонной асимптотыимеетвид |
|
|
|
,где |
|
|
||
|
, |
. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
Еслибыодинизпределов |
lim |
f (x) |
|
или |
lim ( f (x) − kx) не |
|||
x |
||||||||||
|
|
|
x→±∞ |
|
x→±∞ |
|||||
существуетравенбесконечности,токривая |
|
y = f (x) наклонныхасимптот |
||||||||
не. |
0,то b = lim f (x).Поэтому |
|
|
|
|
|||||
|
|
частности,если |
|
|
|
|
||||
|
|
|
x→±∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Уравнение горизонтальной асимптотыимеетвид |
|
|
|
,где |
|
|||
|
|
|
|
|
|
|
|
|
|
|
Пример. |
|
функции y = |
e x |
|
Насимптотыйтиграфика |
|
. |
||
|
||||
|
|
|
x |
|

|
|
|
|
|
|
67 |
|
Решение. |
|
|
|
|
|
|
x = 0. |
1) |
Даннаяфункция |
e x |
– элементарнаяинеопределвточк на |
||||
|
Находим lim |
|
1 |
|
= ∞.Следовательно, |
x = 0– вертикальная |
|
|
|
= |
|
|
|||
|
x |
0 |
|||||
|
x→0 |
|
|
|
|
||
|
асимптота. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2) |
Пусть x → −∞.Тогда k = lim |
e x |
|
0 |
= 0, b = lim |
e x |
− 0 |
x |
|
|||||||
2 |
= |
|
|
|
= |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e x |
|
0 |
x→−∞ x |
− ∞ |
x→−∞ x |
|
|
|
||||||
|
lim |
|
= 0.Знач,прит |
|
x → −∞ |
графикимеет |
|
|
|
|
|
|||||
|
|
= |
|
|
|
|
|
|
|
|
||||||
|
x |
|
|
|
|
|
|
|
||||||||
|
x→−∞ |
|
− ∞ |
|
|
|
|
|
|
|
|
|
|
|
||
|
горизонтальнасимптотую |
|
y = 0. |
|
|
|
|
|
|
|
|
|
|
|||
|
x → +∞ .Тогда |
k = lim |
e x |
|
∞ |
|
|
e x |
|
∞ |
|
|
e x |
|||
Пусть |
|
= |
|
|
= |
lim |
|
= |
|
|
= |
lim |
|
= ∞. |
||
|
|
|
|
2 |
||||||||||||
|
|
x→+∞ x2 |
|
∞ |
|
x→+∞ 2x |
|
∞ |
|
x→+∞ |
|
|||||
При x → +∞ графикнеимеетнаклонныхасимптот.
Общаясхемаисследованпостроенияфункциграфика |
y = f (x). |
1) Найтиобластьопределенияфункции |
2)Выяснить,явлфункцяетсянечетной, иобщегояливида.
3)Насимптотыйтиграфифун. кации
4) Найинтиервалы |
монотонностифункцииееэкстремумы. |
5)Найвыпуклостиин ервалыточкиперегграфифун.бакации
6)Найесл(этвиозможно)точкипересеченияграфифункации осямикоординат.
Пример. |
|
y = |
x2 |
||
Исследоватьфункцию |
|
|
ипостееграфик.оить |
||
x2 |
|
||||
|
|
|
− 4 |
||
Решение. |
1)Функциянеопределенапри |
|
|
|
x = −2 и x = 2.Значит, |
D( f ) = (−∞;−2) (−2;2) (2;+∞) .
2) y(−x) = (−x)2 (−x)2 − 4
симметричтельноотноси
3) Вертикальныеасимптоты:
|
x2 |
||
= |
|
|
= y(x) – |
x2 |
|
||
|
− 4 |
||
Oy . x = −2,т.к.
x = 2,т.к.
функцияявляетсячетной.Ееграфик
lim |
x2 |
# 4 & |
|
|||||||||||
|
|
= % |
|
|
|
|
|
( |
= −∞ |
|||||
|
|
|
|
|
|
|||||||||
x→−2+0 x2 − 4 |
$ |
0 ' |
|
|||||||||||
lim |
|
x2 |
# 4 & |
|
||||||||||
|
|
|
= % |
|
|
|
( |
= +∞ |
||||||
|
|
|
|
|
|
|||||||||
x→−2−0 x2 − 4 |
$ |
0 ' |
|
|||||||||||
lim |
|
|
|
x2 |
# 4 & |
|
||||||||
|
|
|
|
= % |
|
|
( |
= +∞ |
||||||
|
|
|
|
|
|
|||||||||
x→2+0 x2 − 4 |
$ 0 ' |
|
||||||||||||
lim |
|
|
x2 |
# 4 & |
|
|||||||||
|
|
|
= % |
|
|
( |
= −∞ |
|||||||
|
|
|
|
|
||||||||||
x→2−0 x2 − 4 |
$ |
|
0 ' |
|
||||||||||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
68 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Наклонные |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
k = |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
= lim |
|
|
2x |
|
|
|
|
∞ |
= lim |
2 |
|
= 0; |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
(x |
2 − |
|
x |
|
|
3x 2 − 4 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
∞ |
x→±∞ 6x |
|
|
|
|
|
||||||||||||||||||||
b = |
|
|
|
|
x2 |
|
|
|
|
|
x |
|
|
|
|
2 |
|
|
|
∞ |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
0 |
|
lim |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
− |
|
|
|
|
|
|
|
x→±∞ |
− 4 |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Значит, |
y = |
|
|
горизонтальн я |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
4)Находим |
|
y |
|
|
2x(x |
|
4) − |
2x |
= |
|
|
|
− 8x |
|
; |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
− 4) |
|
(x |
2 − 4)2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
yʹ = 0 |
|
|
|
|
|
|
|
|
x = 0 x = 0 |
|
( f ); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
yʹ − |
|
|
|
|
|
|
|
|
, |
|
если |
x2 |
= 0 x = ±2 D( f ).Такимобразом, |
x=0 |
|
– |
||||||||||||||||||||||||
критическаяточка. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x=0 – точкамаксимума, |
|
ymax = y(0) = 0 . |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
+ |
|
|
|
+ |
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
° |
|
|
|
|
|
• |
|
|
|
|
° |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Рис.20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5) yʹʹ |
|
|
|
|
8(x2 |
|
4)2 + 2(x2 |
|
) 2x |
= |
|
24x2 + 32 |
; |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(x2 |
)4 |
|
|
|
|
|
|
|
(x2 − 4)3 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
yʹʹ ≠ |
|
|
.к. |
|
|
|
+ 32 |
; |
|
|
ʹ − не существует, если x = ±2 D( f ).Таким |
|
|
|||||||||||||||||||||||||||
|
|
|
+ |
|
|
|
|
|
– |
|
|
+ |
|
|
|
образом,точекперегибаграфикфунне ции |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
° |
|
° |
|
|
|
имеет.Определимхарактервыпуклости |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
2 |
|
|
|
|
|
наинтервале |
|
(− 2;2) |
– |
функциявыпукла |
|
|
|||||||||||||||
|
|
|
|
|
|
|
Рис.21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вверх;наинтервалах |
|
|
|
|
(− ∞;−2) и (2; ∞) |
– |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
функцвыпуклавн язс . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6)Если |
|
x = 0 |
, |
|
|
y = |
|
пересекает |
|
|
|
|
|
|
|
Оу вточке |
O 0;0 |
y = 0 |
,то |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
).Если |
|
||||||||||||||||||
x = 0 |
.Графикось |
|
|
|
|
|
|
|
|
|
Ох вточке |
( |
). |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O 0;0 |
|
|
|
|
|
|
|
|
|
||||||
Графикизображеннарисунке.
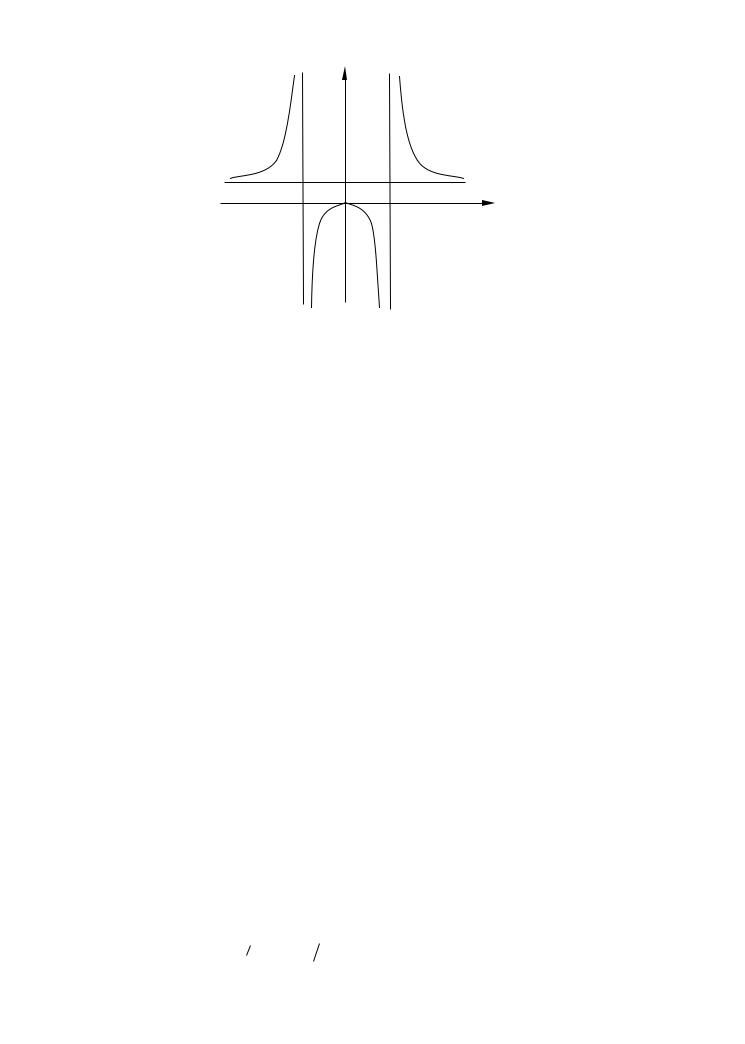
69
y
1
-2 O |
2 |
x |
|
|
|
|
|
|
|
|
|
|
Рис.22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Упражнение 13. |
|
|
|
|
|
|
|
|
|||||||
13.1Сост. уравкасательнитьненкривымуказанныхо:чкахй |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
а) y = |
2x + 3 |
, x0 = 0 ;б) |
x3 + y2 + 4x − = 0, y0 =1. |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
2x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
5x − x2 : |
|
|
|
|
||||||
13.2Сост. уравкасательнойитьненкривой |
й 4x − |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
а)параллельнойпрямо |
|
|
− 2 = 0 ;б)перпендикулярнойпрямой |
|
|
|
|
||||||||||||||||||
2x + 2y − 5 = 0 . |
|
|
|
|
|
|
|
|
|
|
|
y = ln(x −1) ,которая |
|||||||||||||
13.3Сост. уравтойкасательнойитьнениекривой |
|
|
|
|
|
|
|
|
|
||||||||||||||||
образуетсосьюабсциссугол45 |
|
|
|
0. |
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||||||
13.4Накривой. ,заданнойуравнением |
|
|
|
y = |
|
5x + 2 ,н |
айтиточку,в |
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
которойкасаэкривойельнаяимеетуглоэффициентвойк=4. |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
13.5Объемпроизводства. зимнейобуви,выпускаемойнекоторой |
|
|
|
1 |
|
|
|
7 |
|
|
|
|
|
|
|||||||||||
фабрикой,можетбытьописануравнением |
|
|
|
|
u = |
t |
|
t2 + 6t + 2100 ,где t – |
|||||||||||||||||
|
|
|
|
|
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||
календарныймесяцгода.Вычислитьпроизводите |
|
|
|
|
|
|
|
льность,скоростьи |
|
|
|
|
|||||||||||||
тееизменениямп:а)вначалегода;б)вконцегода |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||||||
13.Произво6 трубригадыможетителабытописуравнениемьностьна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
y = −2, 5t2 +15t +100 ,где |
0 ≤ t ≤ 8 - |
рабочеевремячасах.Вычислитескорость |
и t = 7. |
|
|
|
|
||||||||||||||||||
итемпизмен |
|
|
|
енияпроизвотрудапрительности |
|
|
t = |
|
|
|
|
||||||||||||||
13.7Найтипределы. ,ис ользуяравилоЛопиталя:) |
|
|
|
|
|
|
|
|
|
|
lim |
ln2 (1+ x) |
; |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
−2 |
|
|
sin x −cos |
|
|
|
|
|
|
|
|
|
x→0 |
x |
||||
|
|
e |
x |
+ e |
−x |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
||||
б) lim |
|
|
|
;в ) |
lim |
|
;г ) lim |
x |
|
|
) lim x2 (1−e |
|
) . |
||||||||||||
|
|
|
|
|
|
x |
|||||||||||||||||||
|
|
x2 |
|
x −π 4 |
|
2 |
|
||||||||||||||||||
x→0 |
|
|
|
x→π 4 |
|
x→∞ ln(ex +1) |
|
|
x→∞ |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
70 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Домашзадани№1 ее |
3 |
|
|
|
|
||||||||
1Сост. уравкасательитьненияграфифункыхуции |
|
|
|
|
|
|
|
|
|
y = |
2x +1 |
: |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x +1 |
||
а) проходящихчерезточку |
|
|
M(−2; 3) ;б)параллельныхпрямой |
y − x + 5 = 0 ; |
||||||||||||||
в)перпендикулярныхпрямой |
|
|
y + x + 7 = 0 . |
|
|
|
|
|
||||||||||
2Объем. продукции,произведеннбригадойнекоторойраб,м чихжет |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
бытьописануравнением |
|
|
u = − |
5 |
t3 + |
15 |
t2 +100t + 50 , |
1 ≤ t ≤ 8 ,где t – рабочее |
||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
6 |
2 |
|
|
|
|
|
|
|
|
|
|||
времячасах.Вычислитьпроизвоскоростьльностьтруда, иемпе |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
измчечаснрпосленияз |
|
|
еначалаработыизадоеескончания. |
|
|
|
|
|
||||||||||
3Вычислить. пределы, ользуяравилоЛопиталя:) |
|
|
|
|
|
|
|
|
|
lim |
x3 − x + 3 |
; |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ x3 + 3x + 5 |
||||
б) lim |
x4 + 2x2 −3 |
;в) |
lim |
ln 2 −ln(2 − x) |
; г) |
lim |
1+ cos x |
. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||||||||
x→1 x2 −3x + 2 |
x→0 |
10x |
|
|
|
|
x→π (π − x)2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
Упражнение14 |
. |
|
|
|
|
|
|
|||||||
|
14.1Исслед. функциипостроитвать |
2x |
|
|
|
|
|
|
|
ьихграфики: |
ln x |
|
|
|||||||||
1) |
y = x2 (x − 4)2 ; 2) |
y = |
; 3) y = |
x2 |
|
4) y = |
x2 |
|
|
; 5) y = |
; |
|
||||||||||
|
|
|
|
|||||||||||||||||||
|
y = (x +1)e−x ; 7) y = |
x2 +1 |
|
|
x −1 |
|
|
|
x2 −1 |
x |
||||||||||||
6) |
− |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
Домашзадани№ ее |
|
|
14. |
|
|
|
||||||||
|
Построграффун:итькций |
|
x |
|
|
|
|
|
1 |
|
|
|
x |
|
|
|
|
|||||
1) |
y = |
x4 |
− 2x2 ; 2) |
y = |
; 3) y = 2x + |
; 4) y = |
; 5) y = |
ex |
. |
|||||||||||||
|
||||||||||||||||||||||
|
|
|||||||||||||||||||||
|
4 |
|
|
x2 − 4 |
|
|
|
|
|
x2 |
|
|
|
ln x |
|
x |
||||||
