Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Вятская государственная сельскохозяйственная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Ситникова Математика Ч. 1 для менедж

..pdf

Скачиваний:

Добавлен:

25.03.2016

Размер:

24.24 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 96 7 8 9 > Следующая >>>

пр,т.е. дел	lim f (x ∞ или	lim f (x) = ∞, или	lim f (x) =
= lim f (	x −0	x→x0 +0	x→x0 +0
= lim f (	∞.
x→x0 −0

Пример. Точка x0

2 x

Изве,чтосэлемеякаятнофункциянептанарсвоейнаяобласти

являетсяточкойразрывавторогородафункции

,т.к.

lim

= +∞, lim

= −∞.

Видразрывапокнарисункезан

10.

Пример Данафункция

y =

.Требуется:

−

а)

непрерывность функции;

б)определитьродразрыва

вточкеразрыва

;

в)сделатьграфифун. кации

Решение

Даннаяфункцияяв

ляетсяэлементарной.

определения.Даннаяфункция

(− ∞;1) (1;+∞)

следоват,непрерывнаэтихльно

x=1функцияимеет

интервалах.Вточке

разрыввторрода,п госк

олькувэтой

точкеотсутствуютконечные

односторонниепределы:

lim

x→1+0 x −1

= +∞ ,

lim

= −∞.Эскизг

рафика

x→1−0

x −1

функцииизображеннарисунке

11.

Рис.1 1

Упражнения11.

x2 + 2x + 3

x3 −1

11.1пределыфункцииточке. а)

lim

;б)

lim

;

6x + 8

x4 + 2x2 −3

x→1 x2 +1

x→1 x −1

в)

lim

x4 −

lim

;е)

lim

−1

;

x→1 x2 −

x→4 x2

5x + 4

x→1 x2 −3x + 2

x→2

x −2

ж)

lim

;з) li

; и) lim

−

;

x→0

−1

x→2

−

−5

к)

lim

x→8

11.пределы2. функциибесконечности:а)

lim

x2 −2x + 3

;

x→∞ x3 + 7x −1

б)

д)

г)

з)

в)

ж)


lim	2x4 − x + 3		; в) lim	2x4 −3x3 + 5	; г)	lim(	3x4	−3x2 ) ;
x→∞ x3 −8x + 5			x→∞ 3x4 −5x2 +1			x→∞ x2 + 3
lim(		4x4	− 4x2 ) ; е) lim (		−		) ; ж)	lim(	− x) .
lim(			− 4x2 ) ; е) lim (		−		) ; ж)	lim(	− x) .
x→∞ x2 + x + 2				x→+∞				x→∞

11Найти.пределы3. :)

lim ;д) x→0 arcsin 9x

lim 1+ cos x . x→π (π − x)2

11Найтип. 4.

sin 5x

sin2 2x

lim

;б) lim

;в)

lim

;

x→0 4x2

x→0

3x2

x→0 2x

lim

sin 2x + sin8x

;е)

lim

3x2

;ж)

lim

cos x

;

x→0

x→0 cos x −1

x→

x −

2 x

$ 2x2 −1'

7−x3

ределы:а)

lim

+1)1−x

;б)

lim &

)

;

x2 + 4

x→+∞

x→+∞%

(

x + 5

2x +1

&7 x

− 2

'−6 x

1+ 3x

lim%

( ;г)

lim%

( ;д)

lim&

) ;е)

lim

;

x→∞ x +1

x→∞

2x + 5

x→∞ %

5x3 +1

(

x→0 #

x +1

ln(3 − x) −ln3

ln x −ln 4

# 3− 2x2 &−

; з) lim

lim

;к ) lim(16 −3x)x−5 ;

lim%

(

;и )

2x −8

x→0 $ 3+ 3x2

x→0

x→4

x→5

л) lim(sin x)tgx .

x→

11Исследовать.5.фунакцииепрерывность,найтиточкиразрыва

x2 − 25

x2 − 9

x2 + 2

указатьхара:ктерзрыва)

f (x) =

;б)

f (x) =

;в)

f (x) =

;г)

x − 5

x − 3

x − 2

"x − 2, x < 0

%x,

x ≤ 0

x = 0

;д)

f (x) = e x+3 .

f (x) = #2,

f (x) = $1− x, 0 < x ≤1;е)

%x2 − 2, x > 0

x >1

&1− x

Домашзадани№11. ее

1Найти. пределыфункции: 1)

lim

x2 −8x + 7

; 2) lim

x3 −27

;

x→7 x2 −9x +14

x→3 x2 −2x −3

3) lim

−

; 4) lim

−3

; 5) lim

−1

; 6) lim

5x3 + 4x + 3

;

x→0

x→4

−1

x→1 x −1

x→∞ 4x − x3 + 7

7) lim

$ 1

lim

sin3 x

; 8)

lim&

; 9)

lim (

−

) ; 10)

;

x→∞ x2 − 4

x→∞ % x −

1 x2

x→+∞

x→0 2x3

arcsin 5x

; 12) lim

1−cos

2x + 3

&x+1

+ 5

'x2

11) li

; 13)

lim%

(

; 14)

lim&

) ;

x→ arctg10x

x→0

x sin

x→∞

2x +1

x→∞ % x2 − 5

(

ln 2

(2 − x)

ln(5 − x2 ) −ln 5

4x2 −1&

15) li

; 16) lim

; 17)

lim

(

2x2

x→

3x2 −1'

x→0

2Исследовать. фунакцииепрерывность,найтиточкиразрывауказ ть

"x − 2,

x < 0,

− 5x + 6

хара:ктерзрыва

y =

;

= #−2

x = 0 ; 3)

y =

;

x − 4

x > 0

x − 3

x2 −16

%−x − 2,

4) y

x − 4

РАЗДЕЛVПРОИЗВОДНАЯФУНКЦИИ. .ДИФ УНКЦИИЕРЕНЦАЛ
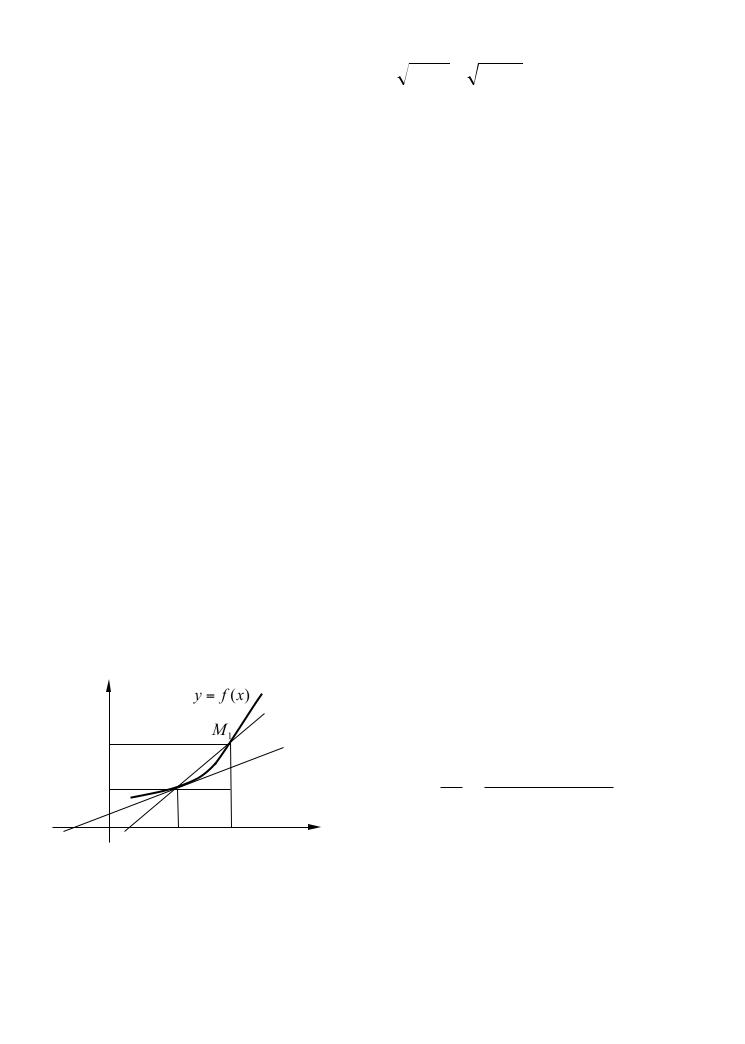
окас
Касательной MN к вданнойточке				называетсяпредельное
положениесекущей		ММ1 ,проходящейчерез		М, когдаточка	М1
неограниченноприближаетсякривойточке				М.
Рассмотрграфнепрерывнойифункциим				y = f (x)(рис.12),
имеющв	й	М невертиккасатаеугловоййдемльную
коэффициент		k = tgα ,где α	уголмеждукасатеиположительнымьной

					Обозначимчерез
y+	y				секущей	ММ1
y+	y			N	углкоэффициентвойсекущейравен:
					углкоэффициентвойсекущейравен:
		M	y				y
	y	M	y		kсек = tgϕ =			=
	y	x			kсек = tgϕ =			=
	α	ϕ					x
	α	ϕ				y = f (
					функции	y = f (

ϕ уголмежду иосьюабсцисс.Тогда

f (x + x) − f (x) . x

x) приращение y тоже

Рис.12			стремикнулю;поэтомуточкася	М1
точке , асекущая		ММ1,пов	неограниченноприближаетсяпокривой	М,пе реходитв
точке , асекущая		ММ1,пов	рачиваяськтолочки	М,пе реходитв
касательную.Угол	ϕ →α ,т.е.		ϕ = α . Следовательно,	lim tgϕ = tgα.
			→0	x→0

Поэтому k = tgα = lim tgϕ = lim		y	= lim	f (x +	x) − f (x)	.
		x
x→0	x→0		x→0		x

Кнахождениюпределоввида	lim	y
Кнахождениюпределоввида	lim	x
	x→0	x
другихзадизачзли	чныхобла:физикистейуки,экономикит.д.в,
котопеременныеых	x и y имеютконкретныйсмысл.Например,взадаче
мгновеннойскорости	x – времядвижения,
произвотрудаительности	x – времяработы,
продукциит..

Обобщаярезультатырешенияподобныхзадач,приходимкпонятию производнойфункции.

Определепроизводнойфункцииие

приводятрешениямножества

y – пройденныйпуть;взадаче
y – объемпроизведенн	ой

Пустьфункция	y = f (x) определенанекотороминтервале		(a;b).
Придадимаргументу	x (a;b) некотороеприращение	x ,	такоечто
x + x (a;b),тогдасамафункцияполучитприращение		y = f (x +	x) − f (x).
Производнойфункции	y = f (x) вточке x называетсяпределотношения
приращенияфункц	иикприращенаргумента,когдаиюргументащение
стремитсякнулюесли(пределсуществует).

Функция y = f (x), имеющпроизвкатждойяинтервалачкедную					(a;b),
называется дифференцируемой наэтоминтервале;опера					циянахождения
производнойфункцииназывается		дифференцированием.
Значениепроизводнойфункции		y = f (x) вточке			x = x0 обозначается
следующимобразом:	f ʹ(x0 )или yʹ(x0 ) .
Геометсмыслпрический		оизводной.Уравнениекасательнойграфику
функции
Взадачепрокасательграфифубылнкнайденуюциигловой			y
коэффициенткасательной		k = tgα = lim	y	.Перепишемэтораввидеенство
коэффициенткасательной		k = tgα = lim	x	.Перепишемэтораввидеенство
		x→0	x
f ʹ(x) = k = tgα ,т.е.		производная f ʹ(x)		вточке	x равнаугловому
коэффицикасательной,проведеннойграфинтукцииу					y = f (x) в
точ,абсциссакоторойеравна		x .
Учитываяэтотфактиспользуяуравнениепрямой,проходящейчерез
заданную точку	M 0 (x0 ; y0 ) сзаданнымуглковымэффициентом				k = f ʹ(x0 ),
получуравнениек емсательной,проведеннойкграфифункуции					y = f (x) в
точкесабсциссой	x0 :	y − y0 = f ʹ(x0 )( x − x0 ).

									55
Нахождениепроизв				однойпоопределению					y = x2.
Пример.		Найтипрофункциизводную							y = x2.
Решение.		Выполнимследействияующ:			x приращение					x ;
1)	придадимаргументу				x приращение					x ;
2)	найдем			y : y = (x +	x)2 − x2 = 2x					x + ( x)2 ;
3)	составимотношение				y	:	y	=	2x	x + ( x)2	= 2x + x ;
3)	составимотношение				x	:	x	=		x	= 2x + x ;
					x		x			x
4)	находимпределэтогоотношенияпри									x → 0:
	lim		y	= lim (2x + x) = 2x .
	lim		x	= lim (2x + x) = 2x .
	x→0		x	x←0
Такимобразом,				(x2 )ʹ = 2x .

Нахождпроизвнениеопосредственноднойопределениюнередко связаносо начительтрудностями,поэтомупрактымифункциике дифференцируютсяпомощьюрядапрформулвил.

Правиладифференцирования

Пусть u = u(x) и v = v(x)– дифференцинанекотоинтервалеомуемые (a;b) функции.Тогда

1)(u ± v)ʹ = uʹ ± vʹ;

2)(u v)ʹ = uʹ v + u vʹ;

3) (С v)ʹ = С vʹ,где							С − const.
u ʹ			uʹ v − u vʹ
4)		=				.
4)		=		v2		.
v				v2
Дифференцированиесложфу кцииой
	Пусть			y = f (u)			и u = ϕ(x) ,тогда y = f (ϕ(x)) – сложфуснкцияая
промежуточнымаргументом							u инезависимымргументом	x .
	Тогдапроизводнаяфункции						y поаргументу	x нахпоследующемудится
правилу:			yʹ	= yʹ	uʹ .
			x	u	x

Формулыдифференцирования

Производныеосновныхэлементарныхфункцийприведенытаблице1.

			2x2	− 4x +1
Пример.	Найтипрофункциизводную: 1)	y =			; 2)	y =	ln x .
				e x

					56
Решение.					(2x2 − 4x +1)! ex − (2x2 − 4x +1)(ex )!
	# 2x2 − 4x +1&!
1)	y! = %		(	=	(ex )2	=
		ex
	$		'

− (2x

− 4x

1)(e

(4x2 1

− 4 + 0)ex − (2x2

− 4x +1)ex

)

− 4(x)

)

−

(ex )2

= −2x2 + 8x −1. ex

Таблица1.

ФУНКЦИЯ y = f (x)

1)y = C − const

2)y = xn , n R

3)y = ex

4)y = ax ,a > 0, a ≠1

5)y = ln x

6)y = loga x, a > 0, a ≠1

7)y = sin x

8)y = cos x

9)y = tgx

10)y = ctgx

11)y = arcsin x

12)y = arccos x

13)y = arctgx

14)y = arcctgx

ПРОИЗВОДНАЯ yʹ = f ʹ(x)

1)yʹ = 0

2)yʹ = nxn−1

3)yʹ = ex

4)yʹ = a x ln a

5)yʹ = 1x

6)yʹ = x ln1 a

7)yʹ = cos x

8)yʹ = −sin x

9) yʹ =

cos 2 x

10)

yʹ = −

sin 2 x

11)

yʹ =

1− x2

12)

yʹ = −

1− x2

13) yʹ =

1 + x2

14)

yʹ = −

1 + x2

2) yʹ = (ln x )ʹ.Здесь u = ln x – промежуточныйаргумент,тогдапо вилу дифференцированиясложфуполучаемнкцииой:

−1

= ( u )

2 u

(ln x)

Логаридифференцированиемическое

Методдиффе,пкоторенцированияпроизводотзаданм аяой функциинаходитсяпомощьюпроизводнойеелогарифма,именно,прежде чемотыскатьпроизводнуюфунк

1	=	1	.
x
		2x ln x

ции y = f (x) еесначалалогарифмируют

ln y = ln f (x)

изатемдифференцируютполучравенствоное

= (ln f (x))! y! = y (ln f (x))! .

Рассмотримприменениедан

ногометонапримередифферена

цирования

степенно-показательнойфункции.

y = xsin x.

Пример.

Найти производнуюфункции

Решение.

Прологарифмируемданнуюфункцию:

ln y = ln xsin x

ln y = sin x ln x.Найдемпроизводнобеихчастейполравенстваученногою:

(ln y)ʹ = (sin x ln x)ʹ

yʹ

= cos x ln x + sin x

sin x

yʹ = y cos x ln x

+ sin x

cos x ln x

+ sin x

Дифференцированиенеявнозаданнойфункции

Функциясчитаетнеявнозаданной, слизадаетсянауравнениемвида

y .

F(x, y) = 0,неразрешотносимымтельно

Придифференцирнеявнозадафункциинаходятпроизводныейвании

y какфункциюот

x ,

правойилевойчастей

уравнения,рассматриваяприэтом

изатемполучравенсразрешаютноевоси ельно

yʹ.

Пример.

Найтипрофункциизво,заданнойуравнениемную

x2 + y2 − 4xy = 0.

Решение.

+ y

− 4xy)

= 0

2x + 2 y yʹ − 4(1 y + x yʹ) = 0 2 y yʹ − 4xyʹ = 4 y − 2x ,такимобразом,

yʹ =

4 y − 2x

2 y − x

2 y − 4x

y − 2x

Производныевысшихпорядков

= f (x) отфункции

y = f (x)

такжеявляетсяфункциейот

Производная

x иназывае

тся произвпервогопорядкадной

			58
Еслифункция		f ʹ(x) дифф,тоепроизводнаяренцируеманазывается			или f	(x) .Т.о.	yʹʹ = (yʹ)	ит.д.
произввторогорядкаднй			иобозначается y	ʹʹ	или f	(x) .Т.о.	yʹʹ = (yʹ)	ит.д.
				ʹʹ		ʹʹ	ʹ
Производнойп		-гопорядка	называетсяпроизводнаяотпроизводной					(n −1)
-гопорядка:	y(n) = (y(n−1) )ʹ.
Пример.	Найтипро зводную		п-го порядфункации			y = e2x .

yʹ = (e2 x )ʹ = 2e2 x ;

yʹʹ = (2e2x )ʹ = 4e2x = 22 e2x ; yʹʹʹ = (4e2 x )ʹ = 8e2 x = 23 e2 x ;

…

y(n) = 2n e2 x .

Понятиедиффункцииеренциала
	Пустьфункция		y = f (x)		имеетвточке				x отличнуюнуляпроизводную
lim	y	= f ʹ(x) ≠ 0.Тогдапоте связиремефункции,еепределабесконечно
lim		= f ʹ(x) ≠ 0.Тогдапоте связиремефункции,еепределабесконечно
x→0	x					y
						y		ʹ			где α → 0 при x → 0,или
малойфункцииможнозаписать						x = f		ʹ
малойфункцииможнозаписать						x = f		(x) +α,
y = f ʹ(x) x + α			x .Первоеслагаемое,равноевыражению								f ʹ(x) x ,
называется главнойчастьюприращения								функции			y .
	Диффункцииеренцалом					вточке				x	назывглавнаяч естсяь
приращенияфункции,равнаяпропроизводнойзведеэтойфункциииюа							dy,т.е.			dy = f (x) x.
приращениеаргумента,обозначается							dy,т.е.			dy = f (x) x.
											ʹ
	Таккакдляфункции			y = x dy = dx =						x ,тоформуладифференциала
приобретает следующийвид:

Изэтойформулыследуравенство

позволяетрассматриватьпроизводнуюкакотношениедифференциалов

Дифферявляфункциейдвухнциалтсяпеременных

Геометрический мыслдиффункцииеренциала

Проведемкграфифункуции	y =
(рис.13)найдемординатуэтойкасадляочкиельной
точки B .

dydx = f ʹ(x),которое,всвоюочередь,

dyи dx

x и dx.

f (x) вточке M (x; y) касательную MN x + x,т.е.ординату


		59
Из АВС имеем:		tgα =	AB	AB = tgα x .Согласногеометрическому
Из АВС имеем:		tgα =		AB = tgα x .Согласногеометрическому
смыслупроизводной,	tgα = f ʹ( . Значит,				AB = f ʹ(x) x.

					формулойдиф ункциеренц, иала
y+ y			В		получаем dy = AB.
y			В	N	Такимобразом,геометрическийсмысл
y	M		dy	N	Такимобразом,геометрическийсмысл
y	M		dy		дифференциалафункциисостов т
		x	А		дифференциалафункциисостов т
		x	А		следующем:	диффункцииеренцал
α					следующем:	диффункцииеренцал
α
					ординкасательнойкграфикуы
	Рис.13				функциивэточкой	е,когда x получит
					приращение	x .

Основныете дифференциалахремы

Основныедифференциалахявляютсяследстправием дифференцирования.

Пример.

Найтидиффункциеренциал

y = ln(1 + e

)

.Вычислить

при

10x

x = 0, dx = 0,1.

10 x

e10 x )ʹ

10e10 x

Решение.

dy = (ln(1+ e

)) dx =

dx =

dx;

10 x

10 e10 0

1+ e

x=0

0,1 = 0,5

dx=0,1

1 + e10 0

Применендифференциалакпр ближеннымвычислениям

x справедливо

Длябольшинфункцийпридостмвалыхточно

приближенноеравенство

,причемэторавттонством,чемнее

y и dy,тополучаем

меньше x .Есливравенствоподставитьвыражениядля

формулу,котораяисподвычисленийьзуется

приближенныхзначений

функции:

f (x + x) − f (x) ≈ f ʹ

x , или

Пример.

Вычислитьприближеннозначение

e1,05 .

Решение.

Рассмотрфункцимю

f (x) = ex .Вышеуказаннаяформула

приобретаетвид:

e x+ x ≈ e x + (e x )ʹ x,т.е.

e x+ x

≈ e x

+ e x

x.Таккак

,топри

x = 1,

x = 0,05

получаем

1,05

0,05 =

+ x =1,05

≈ e

+ e

= e(1 + 0,05) ≈ 2,835.

12Найдите.1производные. функций:

Упражнения12.

y = x4 + 3x2 − 2x +1; 2) y =

−

+ 2 ; 3) y

;

y = 4ex + arctgx + arccos x ; 5) y = 3

+ 4cos x − 2tgx + 3 ; 6) y = x2 log3 x ;

y = (x2 + 2x + 2) 5x ; 8) y =

x2 +1

; 9) y =

; 10)

y =

x ln x

;

x2 −1

1−

1+ x

11) y =

; 12) y = ln(5x2 + 2x5 ) ; 13) y = ectgx ; 14) y =

;

15)

;16) y = sin2 x ; 17) y =

x − 3

; 18) y = ln(ctg(2x2 + 4)) ;

x + 3

19) y = 3arccos2 x ; 20) y = arcctge3x ; 21) y = ctg3

; 22) y = arcsin2

;

23) y = log7 cos

12Найти.про2. функцийзводные,испл льзуягарифмическое

дифференцирование:

y = (sin x)tgx ; 5)

y = xx3 ; 2) у = х

; 3) у = х

ln x

; 4)

y = x−xe−2 x ;

y =

(2x −1)3

)

12Найти.3про. неявнозадаводфункций: ыеых

x ln y + y ln x = 0 ; 2)

x cos y − ysin x = 0 ; 3) xy − arctg

= 0 ;

4) ex + ey − exy −1 = 0 .

Найтипрофункцийзводные:

Домашзадани№12. ее

y =

−

+ 2 ; 2) y =

arctgx ; 3)

y =

cos x

; 4)

y =

;

1+ 2sin x

" x2 %

3−tg2 x

; 7) y = arccose

−x2 2

y = log7 (cos

y = ln$

' ; 6)

=10

; 8)

;

#1− x2

<<< < Предыдущая 1 2 3 4 56 / 96 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.11.2019270.97 Кб11Реферат педиатрия.doc
#
11.07.2019129.02 Кб4РЕШЕНИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ СИМПЛ....doc
#
19.11.2018412.67 Кб4Родыгин А.Д. Логика.doc
#
27.08.2019759.81 Кб6Сборник задач 2012.doc
#
27.05.2015165.89 Кб9сельхозпредприятия.doc
#
25.03.201624.24 Mб13Ситникова Математика Ч. 1 для менедж..pdf
#
12.09.2019334.85 Кб13Сквозная задача по налогообложению.doc
#
27.05.2015219.76 Кб6Содержание.doc
#
10.07.201949.66 Кб2Социология (1 семинар).doc
#
12.11.20192.64 Mб6статистика_лекции_2.rtf
#
20.09.2019841.87 Кб5Статья Содержание и процедуры составления конс...rtf