Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Вятская государственная сельскохозяйственная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Ситникова Математика Ч. 1 для менедж

..pdf

Скачиваний:

Добавлен:

25.03.2016

Размер:

24.24 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

												21
2 − 1 3			− 5		1	1			−1 − 5 0				2
2 − 1 3			− 5		1	1			−1 − 5 0				2
	1	− 1 − 5	0		2			2		1 3		− 5	1			2 Ι
	1	− 1 − 5	0		2			2	−	1 3		− 5	1	−		2 Ι
	3	− 2 − 2 − 5			3			3	− 2 − 2 − 5				3		− 3 Ι

	7	− 5 − 9 − 10			8			7	−	5 − 9 −10			8		−	7 Ι
	7	− 5 − 9 − 10			8			7	−	5 − 9 −10			8		−	7 Ι
1 − 1 − 5 0				2						1 −1 − 5 0							2
1 − 1 − 5 0				2						1 −1 − 5 0							2
	0	1 13 − 5		− 3							0 1 13			− 5
	0	1 13 − 5		− 3							0 1 13			− 5			− 3
	0	1 13 − 5		− 3			− ΙΙ				0 0	0		0			0	.

	0	2 26 − 5		− 6			− 2 ΙΙ				0 0	0		0			0
	0	2 26 − 5		− 6			− 2 ΙΙ				0 0	0		0			0

Посколькуранг			асширеннойматрицысистеравенрангуатрицы
системы,тоСЛАУсовмсм.(тестнаКронекераема					-Капелли),таккак
количествонеизвестных(4)большеранга(2),тосистемаимб сконечноеет
множестворешений.
Отполученступематрицысновачатойперехо					димксистеме:
x1 − x2 − 5x3		= 2	.
		= −3
x2 +13x3 − 5x4				x2 : x2	= −3 −13x3 + 5x4 .Переменные,
Изпоследнегоуравнениявыражаем
оказавшиесяправойчасти(				x3 , x4 ),считаемсвободныминаходимизпервого		x1 :
уравнениявыражениечерезсво				бодныепеременныедля
x1 = x2 + 5x3 + 2 = (− 3 −13x3 + 5x4 )+ 5x3 + 2 = −1−8x3 + 5x4 .
Ответ: (	x1 = −1 − 8x3 + 5x4 ;			x2 = −3 −13x3 + 5x4 ;	x3 ; x4 ),где x3 , x4 R –	общее

решениесистемы.

Придавая свободнымнеизвестнымразличныечисловые начения,можно получитьчастныерешенияданнойсистемы.

Упражнения4.

4Реши.1сис. матреьметиупочнымправилудоКрамера:

	"x − x		2	+ x		3	= 6			"4x
а)	$	1								$	1
	#x1 − 2x2 + x3 = 9 ;б)									#5x1
	$x − 4x			2	− 2x			3	= 3	$3x
	%	1								%	1

4Реши.2сис. методомГаемуь: сса

4Решит.3. ьсистелюбымизтрехметодову:

4Исследовать.4. совмесиистнайтиностьобщеемырешение:

+2x2 − x3 = 1

+3x2 − 2x3 = 2 .

+2x2 − 3x3 = 0

"$3x1 + x2 + 3x3 = 2

#5x1 − 2x2 + 2x3 = 1. $%2x1 + 2x2 + 3x3 = 1

!3x1 + 4x2 = 11

5x2 + 6x3 = 28.

#x1 + 2x3 = 7

	"x − 2x				+ 3x − x											= 9								"x − x				− 3x						− 4x								= 1
	$	1		2						3					4			= 5						"x − x			2	− 3x					3	− 4x							4	= 1
а)	$4x + 3x						− x + 2x											= 5			; б)			$	1		2						3								4							= 2 ;
а)	#	1			2					3						4					; б)			#2x − 2x						2	+ 2x					3			+ 3x						4			= 2 ;
	$2x1 − 5x2 + 3x3 + x4 = 16																								1					2						3									4
	$2x1 − 5x2 + 3x3 + x4 = 16																							$−x + x −13x −18x = −1
	$4x + 6x + 2x − x = 5																							%	1			2							3											4
	%	1			2						3					4									"2x − x							+ 4x								+ x							= 9
	"x − x			+ 3x						+ x					= 6										"2x − x						2	+ 4x						3		+ x				4			= 9
	"x − x		2	+ 3x					3	+ x				4	= 6										$	1		2x			2	− 3x						3						4			= −1
	$	1	2						3					4											$															− x
в)	$						− 7x						− x					= 8 ; г)							$x −						2						3			− x			4							;
в)	#7x + 5x					2	− 7x					3	− x				4	= 8 ; г)							#	1					2						3						4							;
		1				2						3					4		= −6						$2x1 + x2 + 4x3 − x4 = 11
	$x + 8x			2		−18x					3		− 5x					4	= −6						$2x1 + x2 + 4x3 − x4 = 11
	%	1		2							3							4							$		− 2x2 + x3													− x4 = 9
	"6x + 4x							+ 5x						+ 2x						+ 3x					%3x1		− 2x2 + x3													− x4 = 9
	"6x + 4x						2	+ 5x					3	+ 2x					4	+ 3x			5	= 1
	$	1					2						3						4				5
	$							− 2x3						+ x4 = −7
д)	$3x1 + 2x2							− 2x3						+ x4 = −7									= 2 .
д)	#9x + 6x						2	+ x			3		+ 3x					4	+ 2x			5	= 2 .
	$	1					2				3							4				5
	$							+ 4x3						+ x4 + 2x5									= 3
	%3x1 + 2x2							+ 4x3						+ x4 + 2x5									= 3
		4Фирма.5сост. издвухотделенийит,суммавеличинапрнаяибыли
которыхв									минувшемгодусоставиламлн12																																									руб.Натекущийгод
запланиувеличениерпервибылиованоотднаго70%,ленияавторогона
40%Врезульт.суммарнаяприбдолжнатевывльрасти																																																			1,5раза.Какова
величинаприбылиотделенийм годунувшемэто?ду
		4Швейная.6.фабрикатечетрехднпроизводилаиеейкостюмы,плащи
куртки.Известныобъемывыпускапродукциизатратына этизводство
днив(у.е.)Н. айтисебестоимост																										ьединицыпродукциикаждоговида.
		День									Костюмы												Плащи					Куртки														Затраты
		Первый														50									10							30																	176
		Второй														35									25							20																	168
		Третий														40									20							30																	184
		4Дана.7мат. прзатратямыхица																																							!0,1								0, 5		.НаймаХтрицу	для
		4Дана.7мат. прзатратямыхица																																A = #								0,3								&	.НаймаХтрицу	для
																															!400											0,3							0, 2%
обеспечеконечпродукциинойия																															!400
обеспечеконечпродукциинойия																										Y = #										&.
																																500%
		4Работа.8си. ,стемыостиздвухотраслейящ, нч ниекоторого
периодахарактследризуующимианнымиусл.(д.е.тсяд)Вычислить.
матпрзатратямыхицу.
		Отрасль																	1						2				Валовыйпродукт
					1													100						160																	240
					2													275							40																	85
		4Имеютсяданные.9. оработе																										системыдвухотраслпрошломпериодей
ипланвыпускапродукцииУ																									1 вбудущемпериоде.																									Найтивалопродуктвый
планпери,обеспечивающмодевыпускпродукцииУ й																																																			1.

			23
Отрасль	1	2	Валовыйпродукт		ПланУ			1
1	80	120	500		350
2	70	30	300		300
			Домашзаданиее	№4.
1Реши. сислинейныхтемуьуравнтремя:тодаминийматричным				"x + x			− 2x			= 6
				"x + x		2	− 2x		3	= 6
				$	1	2			3
мет,пфордомКрамераиметодомуламГаусса				#2x1 + 3x2 − 7x3 = 16 .

$%5x1 + 2x2 + x3 = 16

2Исследова. совмес,найоднообщеетностьи дночастноерешение системыуравнений:

	"x − x			2	− 3x					3	− 4x				4		= 1							"x + 3x		2	− 3x			3	= 2
	$	1		2						3					4									$	1	2				3
а)	#2x1 − 2x2 + 2x3 + 3x4 = 2 ;б)																							#4x1 + 4x2 − 4x3 = 5 ;
	$−x + x				2		−13x						3	−18x					4	= −1				$	−x − 5x			2	+ 7x			3	= −1
	%	1			2								3						4			= −4		%	1			2				3
	"x + 2x					2		+ x			3	+ 4x					4	+ x			5	= −4
	$	1				2					3						4				5
	$								+ x					+ x				− 3x					= 1
в)	$3x + 2x							2	+ x			3		+ x		4		− 3x				5	= 1	.
в)	#	1						2				3				4						5		.
	$		x2 + 2x3 + 2x4 + 6x5 = −1
	$		+ 6x2 + 3x3 + 9x4																	− x5 = −7
	%5x1		+ 6x2 + 3x3 + 9x4																	− x5 = −7

3Обувная. фабрикаспециализирповыпускизделийтрехвидов:уется
сапог,кроссовокиботинок;приэтомспользуетсясыртиповехьеS				1, S2 , S3.
Нормырасхокажизнихднаоднуогопарубиобъемвир				асходасырьяна1
деньзадтаблиц.ныНайтиежеобъемдневныйвыпускакаждоговидаобуви.
Видсырья	Сапоги	Кроссовки	Ботинки	Расходсырьяна1
				день,усл.ед.
S1	5	3	4	2700
S2	2	1	1	800
S3	3	2	2	1600

4Втабл. приданныецевобисполненииденыбалансаза				отчетный
период,усл. . .н:
Отрасль	1	2	Конечный	Валовый
			продукт	выпуск
1	100	160	240	500
2	275	40	85	400
Вычислитьнеобходимыйобъемваловоговыпускакаждойотр,еслисли
конечныйпродуктпервойотраслидолженувеличитьсяр2,автоза				ройна
20%.

						24
РАЗДЭЛЕМЕНТЫІІ. МАТРИЧНОГО
Оснпонятиявекторнойныеалгебры
	– это отрезок,имеющийопределенную
длинуопределенноенаправление.Обознач								или	,где А – начало
вектора,	а	– егок .Вектор				BA называется противоположным вектору
AB .Вектпротивоположный, вектору						a ,обозначается –
		или			модулем	AB	называетсяотрезка		АВ и
обозначается			AB	.Вектдлинаора ,называется					нулевым

векторомиобозначается					0 .Вект,длинаораторогоединицевна,называется
единичным .
Векторы			a и b			коллинеарными,ес наодной
прямойилинапараллельнпрямых;записых								a	b .Коллинеарные
векторымогутбытьнаправод наковопротивоположноены.						равными, еслиониколлине,
Двавектораназываются						равными, еслиониколлине,		рны
направлеиимеютодидлины;аковые							,	= b
Тривектораназываются							,		есонилежат
воднойплоскостиилипара лельныхоскостях
Линейныенадвекторами
Клинейнымоперациямнадотносятся:сложение,
векторвектораиумнонажениечисло.
			конечногочисла			векторов	a + b	+ c	вектор,
соединяющийначапервогослагаемогове тораонцпоследнего, м
слагаемыевекторытаким,чтоон
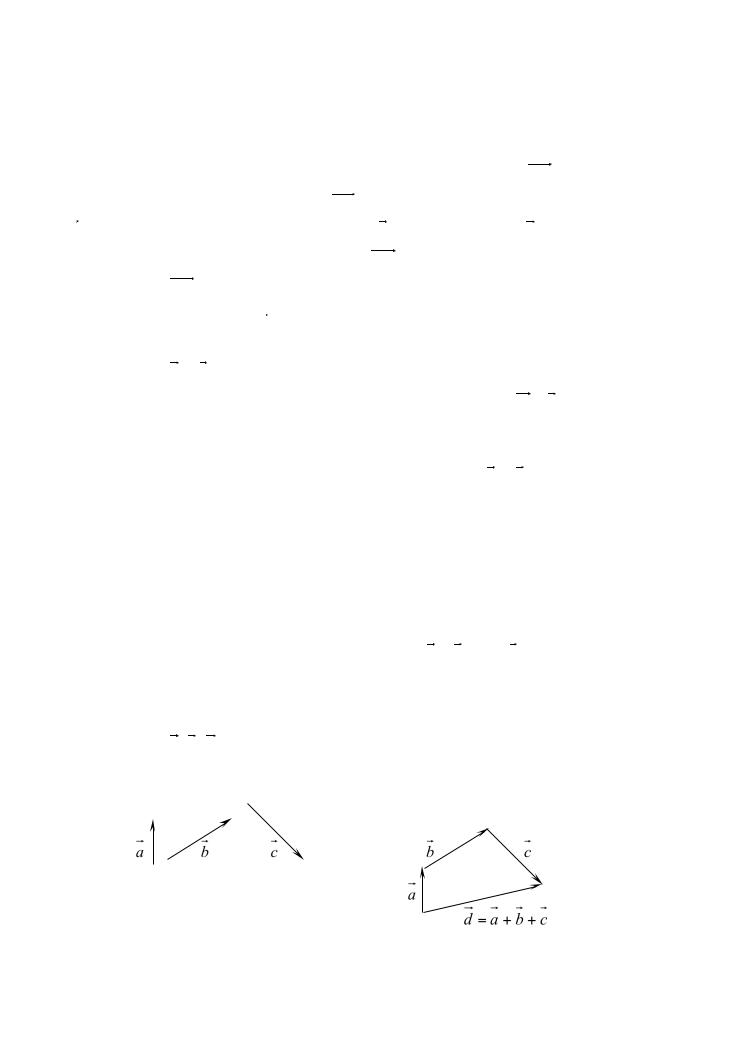
векторасовпначаломдает.Нарисункпоказано1 сложение
трвехкторов			a, b, c.

Рис.1

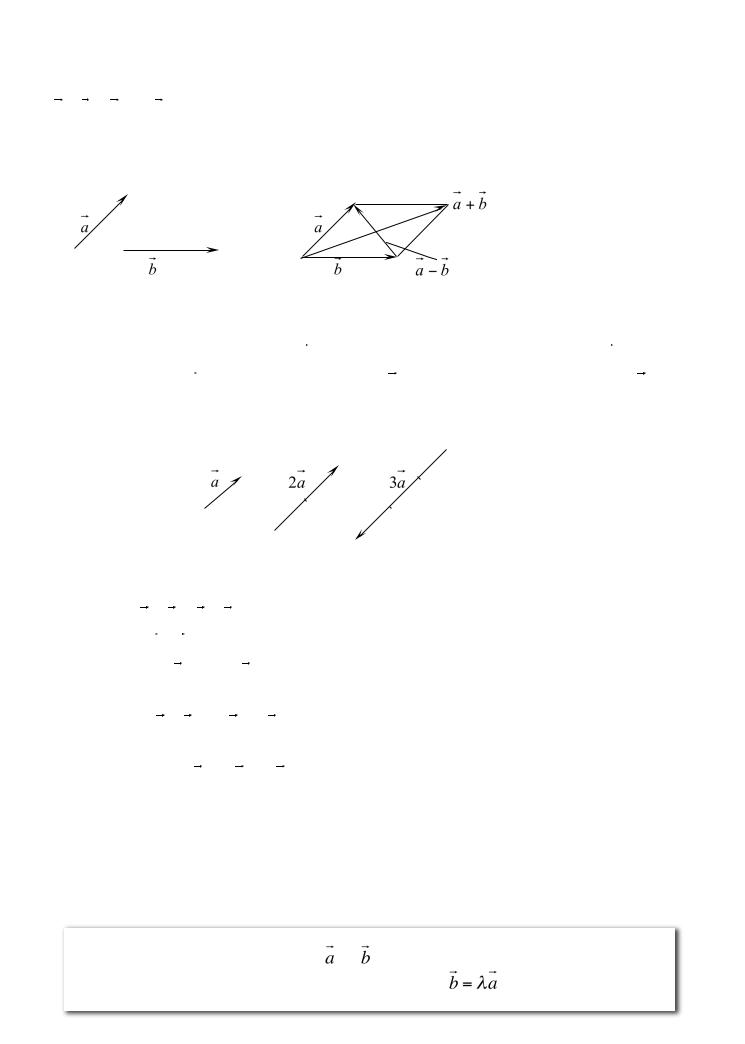
Вычитание векторовсвестисложениюпоследу:

a − b =	(−b).
нахождеиразнвииухекудобнотпользоваться
,	котороеиллюстрирует

Рис

			a число	λ ≠	вектор	λa ,который
имеетдлину	λ	a	коллинеарен	, имеетнаправление		a , если
имеетдлину	λ	a	коллинеарен	, имеетнаправление		a , если

λ > 0,ипротивоположное,если				λ .
Пример.			2а и

–

Рис.3

подчследующимсвойствамнны

a + b =

коммутати;

ое

(a + b)+

+ (

) –

сложенияв

λ(µa)=

–

умноженияотносительно

множителя;

λ(a + b)

λb –

тноси

льносуммы

;

(λ + µ)a

+ µa –

св йствотносительно

множителей.

Двавектора

коллтогданеарнытогда,

когдапри

равенство

b = λa

	Изопредел начиследуетя	условие
коллинеарнвекторовсти		:

	Дваненулевыхвектора	и коллтогдаитольконеарнытогда,
	когдапринекотором	λ≠0 верно равенство

	26
Координатывектора.	Линейные операции,длинавектора,условие
коллинеарностивекторовкоординатах
Пустьвпространсдекарсистемекооровойвеннзадтвеаионйчкиыат
M1(x1; y1; z1 ) и M 2 (x2 ; y2 ; z2 ),являющиеся,соответственно,началомконцом
вектора M1M 2 = a .Тогда	координатвекторами	a будемсчитатьчисла

(ax ;ay ;az ),где ax = x2 − x1;ay = y2 − y1;az = z2 − z1.Записывают a(ax ;ay ;az ).

Длинавектора : a = ax 2 + ay 2 + az 2 .

Пусть a(ax ;ay ;az ), b(bx ;by ;bz ).

Тогда

a + b(ax + bx ;ay + by ;az + bz );

a −b(ax −bx ;ay −by ;az −bz );

λa(λax ;λay ;λaz ).

Условиеколлинеарности			векторов a и b естьпропорциональностьих
соответствующихкоординат:	a	x	=	ay		=	a	z	.
соответствующихкоординат:	b		=	b		=	b		.
	b	x		b	y		b	z
		x			y			z
Скалярноепроизведениевект,угмеждувекторамировл,условие
перпендикулярностивекторов
Скалярнымпроизведением			двухненулевыхвекторов							a и b называется
число,равнпроиздлинеэтихвектдениюнаоугласинусровме										ждуними.

где ϕ – уголмеждувекторами

a и b .

Пусть a(ax ;ay ;az ),

b(bx ;by ;bz ),тогда

a b = axbx + ayby + azbz .

Используядействиескалумножениярноговект,можнонайтировуг л

междувекторами

a и b :

cosϕ =

a b

axbx + ay by + az bz

ax2 + a2y + az2 bx2 + by2 + bz2

Условиеперпендикулярности

ненулевыхвекторов

a и b :

a b axbx + ayby + azbz = 0.

							Упражнения 5.
5.1Поданным. векторам				1		1	a и b построитькаждыйизследующих
	!	1	! !	1	!	1	! !
векторов:	3a, −		a, 2a +		b,		a − 3b .
векторов:	3a, −	2	a, 2a +	3	b,	2	a − 3b .
		2		3		2

5.2Даны.точкиА(3;

-1;иВ2)(3;

-4;Найти6)длинувектора.

АВ иего

направляющиекосинусы.

a(2;−3;−1) , еслиегок нец

5.3Определить. :а)координначалавектораты

совпадаетсточкойВ(1;

-1; 2); б)координатыконцавектора

a(3;−1;4) ,еслиего

началосовпадаетАчкой(1; 2;

-3).

5.4Даны.двекоординатывекторах=4,у

-12Опред. еготретьюлить

коордлинау,ес вектора13вн.

z углы, соответственно, 1200 и45 0.

5.5Вект.составляетрсямиОх

КакугонсоставляетйосьюОу?

5.6Вектор.

а составляеткоординатнымиосямиОхОууглы60

0 и120 0.

Вычислитьегок ординаты,если

= 2 .

5.7Определить. ,прикакихзначенияхпараметров

α и β векторы

a = −2i + 3 j + βk и b = αi − 6 j + 2k

коллинеарны.

5.8Найтискалярное. произведениевекторов

а и в ,если :

1) a(2;−3; 4), b(3;−1;−2); 2) a(2;3; 4), b(−2; 4;−2) .

5.9Определить. уголмеждувекторами: 1)

a(1;1;−4), b(1;−2;2) ;

2) a(2;3;−1), b(13;−6;8) .

m векторывзаимно

5.10Определить. ,прикакомзначениипараметра

перпендикулярны a(m, −3, 2), b(1, 2, −m) .

5.11Данывершины. треугольникаА(0;В(1;0;С( 1;5); 1);

-1; 2;

3).

Показать,чтоонпрямоугольный.

5.12Вычислитьвнутренние. углытреугоАВС,еслиьника

А(7; 4; -2),В(3;

-1; 7),С(1; 2;

1).

Показать,ч реугольни

кАВС

–

равнобедренный.

a(4;−2;−4), b(6;−3;2).Вычислить:

(2a − 3b)(a + 2b),

5.13Данывекторы.

(a + b)2 .

(5a + 3b)(2a − b) ,если

= 2,

= 3, a b .

5.14Вычислить.

5.15Вплоск. находятривекстиорася

a, b, c .Известно

= 2,

= 3,

= 5, (a,b) = 600, (b, c) = 600 .Найтидлинувектора

d = −a + b − c .

	Домашзадани№5 ее	.
1Данывекторы. :	a(4; − 2; − 4), b(6; − 3; 2) .Вычислить: 1)		a b; угол2)
междувекторами	a и b ; 3) (2a − 3b) (a + 2b); 4) (a + b)2 .

2Векторы.

и b образуютугол

α = 600 ,известно,что

= 3,

= 4 .

Найти:

а)

(3a + 2b) (a − 2b) ;б)

(3a + 2b)

Данывершинычетырехугольника

A(1; − 2; 2), B(1; 4; 0), C(−4; 1; 1) и

D(−5; − 5; 3) .Доказ,чтодиачетыргоналитьперпендикулярныхугольника.

4Найти. длинысторонуглытреугольникасвершинами

A(2; 1; 3), B(5; 2; −1) , C(−3; 3; − 3) .

5Данывекторы.

a = 6i −8 j + 5

k и

b = 2i − 4 j + k .Найтиугол,

образуемыйвектором

a − b сосьюО

Вектпространстворное

n-мернымвектором

называетсяупорядсовоченкупнаяость

действительныхчисел

a1 = (a11;a12 ;…;a1n ),где

а1i –

i-аякомп

онентаили

координатавектора

a1 (i=1, 2, …, n).

n-мерныйвекторможетбытьрассмотренкакобобщениевектора

n-мерноговекторнпространства,подго

трехмерногопространстванаслучай

которымследуетпониматьсовокупность

n-мерныхвекторов

c определенными

вданнойсов купностиперациясложениявекторвекторам онажения

число.Праввыполнениясвойствалаэтихоперацийнамибылиизложены

длявекторовтрехмерногопространства.

Вектор ат называется линейнойкомбинацией

векторов a1 , a2 ,…, am−1,если

am = λ1a1 + λ2a2 + …+ λm−1am−1,где

λ1,λ2 ,…,λm−1 – некоторыечисла.

Векторы a1 , a2 ,…, am называются линейнозависимыми,

еслиуществуют

такиечисла

λ1 , λ2 ,…, λm ,неравныеодновременнонулю,что

λ1a1 + λ2 a2 + …+ λm am = 0 (*).

λ1 = λ2 = … = λm = 0,

Еслиравенс(*)выптольковоприусловииняется

векторы

a1, a2 ,…, am называются линезависимымийно

Вектпространстворноеимеетразмерность

n иназывается n-мерным,если

оноимеет

n линейно независимыхвекторов,приэтомлюбые(

n+1)векторов

являютсяинейнозависимыми.

Базисом n-мерноговекторногопространстваназысо окупностьают

линезависимыхйновекторов.

e1 ,e2 ,…,en

n-мерного

Пустьвекторы

образнекоуютисорого

векторногопространс,тогдалюбойвекторва

а1 этогопростраможноства

разлпэтомубазисужить

,т.е.представитьследующемвиде

a1 = a11e1 + a12 e2 + …+ a1nen ,где

а1i – координатывектора

а1 взаданномбазисе.

Пример.

Данывекторы:

a1 (1;1;1),

a 2 (0;2;3), a3 (0;1;5),

a4 (2;-1;1).

1) Показать,

чтовекторы

a1 ,

a2 ,

a3 образтрехмеуютиспространства;разл2)ногожить

вектор a4 поэтомубазису. Решение.Заме,чтобазисрехмерногоимпросостоитрансизвекторов3 . ва

1)Длядоказатого,чтовекторыельства

a1 , a2 , a3

образуютис

пространства,доста

точнопоказатьлинейнуюзависимостьэтойсистемы

λ1a1 + λ2 a2 + λ3a3 = 0 .

векторов.Дляэтогосоставимвекторравеноество

Записывая

a1 , a2 , a3

ввидевектор

-столбцов,получим

.Задачасвелась,такимоб,разомешениюсистемы

λ1 1 + λ2

+ λ3

λ1 = 0

+ 2λ2

+ λ3

= 0 .Решаяданнуюсистему,получ,чтоонимаемет

λ1

λ + 3λ

+ 5λ

= 0

= 0.Значит,системавекторов

a1 ,

единулевоественрешениеое

λ1 = λ2 = λ3

a2 , a3 линезависимайно,т..образтрехмерногоуетпространства.

2)Дляразложениявектора	a4 побазису	a1 , a2 ,	a3	нампонадобится
решитьуравнение	a4 = λ1a1 + λ2 a2 + λ3a3 относнеительнозвестных					λ1 ,λ2 ,λ3.
		λ1 = 2
Уравнение a4 = λ1a1 + λ2 a2 + λ3a3 равносистеме: ильно						+ λ3 = −1.
Уравнение a4 = λ1a1 + λ2 a2 + λ3a3 равносистеме: ильно		λ1 + 2λ2				+ λ3 = −1.
		λ + 3λ			2	+ 5λ = 1
			1		2	3
Находимрешениесистемы:	λ1 = 2 , λ2 = −2, λ3 =1.
Такимобразом,	a4 = 2a1 − 2a2 + a3 .

Упражнения 6.

6.1Выяснить. , явлвекяюилинейнотсязависимымиоры:

1)a1 = (4; − 5; 2; 6), a2 = (2; − 2;1; 3), a3 = (6; − 3; 3; 9), a4 = (4; −1; 5; 6) ;

2)a1 = (−1; 7;1; − 2), a2 = (2; 3; 2;1), a3 = (4; 4; 4; − 3), a4 = (1; 6; −1;1) .

6.2Даны.векторы		a = 2i + j , b = i − j + 2k ,		c = 2i + 2 j − k и d = 3i + 7 j − 7k .
Необходимо:а)доказа,чтовектоьры		a, b и c		образиразложитьуютис
вектор d поэтомубазису;		)доказа,чтовектьоры		d, b и c образи уютис
разложитьвектор	a поэтомубазису.
6.3Внекотором. базиседанывекторы
a1 = (−2; 0; 1), a2 = (1; −1; 0), a3 = (0; 1; 2) . Выяснить				,	явлвекторяетсяи
a4 = (2; 3; 4) линейнойкомбинациейвекторов			a1, a2, a3 .
6.4Внекото.		ромбазиседанывекторы
a1 = (1; 2; 1), a2 = (2; 1; 1), a3 = (−1; − 2; −1) .Найтивсезначения					m,прикоторых
вектор b = (2; 3; m) линейновыражаетсячерезвекторы					a1, a2, a3 .
6.5Предпр. выпускает4продукцииятиедаколичествах50; 80; 20
120ед.Приэто	нормырасыхорьядаставляютсоответственно7;и3,5; 10
4кг.Определитьсуммарныйрасходсырьяегоизменениепри		ниях
выпускапродукции	, соответственно, на+5;		-4;-2и+10ед.

		30
6.6Даны.векторы		e1, e2, e3 ,образующиеортонормиров	анныйбазис.Найти
уголмеждувекторами		x = 5e1 + e3 и y = e1 + e2 + e3 .
		Домашзадани№6 ее	.
1Выяснить.		, явллинейнояютсязав с нейномыми
независимвектор: ыми
а)	a1 = (−7; 5;19), a2 = (−5; 7; − 7), a3 = (−8; 7;14);
б)	a1 = (1; 8; −1), a2 = (−2; 3; 3), a3 = (4; −11; 9) .
2Данывект.		оры a1 = (1;1;1), a2 = (0; 2; 3), a3 = (0;1; 5).Доказа,чтовекторыь
a1, a2, a3 образ.Найтиуютискоординатывектора			d = (2; −1; 1) вэтомбазисе.
3Данывекторы.		e1, e2, e3 ,образующиеортонормированныйбазис.Найти
уголмеждувекторами		x = 3e2 − e3 и y = 4e1 + e2 − 2e3 .

РАЗДЕЛІІІ.ЭЛЕМЕНТЫАНАЛИТИЧЕСКОЙГЕОМЕТРИИ
Уравлинаииплоскостиение
Уравненлиниием	наплоскостиназываетсяуравотносендвухительно
переменных x и y, которомуудовлетворяюткоординатылюбой		точки М (x; y)
даннлиниитоонийлько.		L наплоскостиможнозаписатькак
Вобщемвидеуравнениелинии		L наплоскостиможнозаписатькак
F (x; y) = 0.

Такимобразом,справедливоутверждение:

Изэтогоутвержденияследуютвадляжныхпрактикиположения:
1)Еслизаданоуравнениелинии,томожноустановить,при		надлежитли
этойлиниикакая	-либоточкаплоск.Дляэтдосстиго	татпочнодставитьее
координатывуравнениелиниивместопере		менных x и у.Еслиокажется,что
ониудовлеуравнениюряют,тто		чкапринадлежитлинии,впротивном
случае - непринадлежит.
2)Координатыточкипересечениядвухлиний,заданныхсвоими
уравнениями	F1 (x; y) = 0 и F2 (x; y) = 0 , удовлетворяютуравнениямобеих
линий.Поэтомудлянахождениякоординатто		чекпересечениядвухлиний
нужнорешисис, оставлеемуьизуравэтлиний:нуюенийх		F1 (x; y) = 0
		F (x; y) = 0.
		2

Чтсобыставуравнениел какниисовокупноститьточек,обладающих
некоторымсвойством,исключительноприсущим,необходимо:		x и y;
1) взятьпроизволь	нуюточкулиниистекущимикоординатами

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.11.2019270.97 Кб11Реферат педиатрия.doc
#
11.07.2019129.02 Кб4РЕШЕНИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ СИМПЛ....doc
#
19.11.2018412.67 Кб3Родыгин А.Д. Логика.doc
#
27.08.2019759.81 Кб6Сборник задач 2012.doc
#
27.05.2015165.89 Кб9сельхозпредприятия.doc
#
25.03.201624.24 Mб13Ситникова Математика Ч. 1 для менедж..pdf
#
12.09.2019334.85 Кб13Сквозная задача по налогообложению.doc
#
27.05.2015219.76 Кб6Содержание.doc
#
10.07.201949.66 Кб2Социология (1 семинар).doc
#
12.11.20192.64 Mб6статистика_лекции_2.rtf
#
20.09.2019841.87 Кб5Статья Содержание и процедуры составления конс...rtf