Введение

В информационных системах различного назначения полезные сигналы поступают всегда на фоне помех различного происхождения. Под помехой будем понимать 1 любое воздействие на полезный сигнал, затрудняющее его прием и регистрацию. Для уверенного обнаружения полезных сигналов и измерения тех или иных их параметров необходимо обеспечить достаточное превышение энергии сигнала над энергией помех. Но при современном состоянии схемотехники информационных систем резервы повышения энергии полезного сигнала практически исчерпаны. Кроме того, некоторые помехи, например, реверберационная, растут одновременно с увеличением сигнала.

Поэтому наиболее верный путь развития информационных систем заключается в оптимизации режимов обработки принимаемого сигнала с целью максимального увеличения отношения сигнал / помеха. Это может быть достигнуто прежде всего использованием фильтров с оптимальными частотными и импульсными характеристиками. Поскольку все чаще задача обнаружения полезного сигнала возлагается на автоматические устройства, очень важной оказывается также разработка оптимальных алгоритмов обнаружения и обнаружителей, реализующих эти алгоритмы. Это обосновывает необходимость изучения студентами направления «Приборостроение» вопросов обработки сигналов с учетом специфики использования соответствующих приборов и систем.

1. Фильтрация сигналов на фоне помех

1.1. Постановка задачи фильтрации

Пусть на входе системы действует колебание

x(t) = F [s(t,l), n(t)],

где s(t,l) – полезный сигнал, n(t) – помеха, l – совокупность интересующих нас параметров l_i(t), причем сам сигнал s(t,l), или параметр l_i(t) – случайные процессы. Помеха n(t) может быть произвольной; сигнал и помеха не обязательно представляют собой аддитивную смесь. Считается, однако, что вид функции F (т. е. способ комбинирования сигнала и помехи) и некоторые статистические характеристики случайного сигнала и помехи нам известны. С учетом этих априорных сведений нужно решить, какая из возможных реализаций самого сигнала s(t, l) или его параметра l содержится в принятом колебании x(t). Из-за наличия помех и вследствие случайного характера сигнала оценка реализации сигнала или его параметра зачастую не будет совпадать с истинным значением, что приводит к ошибкам фильтрации. К тому же к фильтрам, предназначенным для использования в различных устройствах, предъявляются различные, порой противоречивые требования. Поэтому и характеристики фильтров должны удовлетворять различным критериям. Фильтры, предназначенные для устройств обнаружения, должны обеспечить максимум отношения сигнал/помеха. Фильтры, предназначенные для устройств измерения тех или иных параметров, должны отвечать критерию минимума среднеквадратической погрешности. Возможны и другие виды критериев, по которым строятся характеристики.

1.2. Оптимальные фильтры устройств обнаружения

Оптимальные линейные фильтры широко применяются при обнаружении и различении детерминированных сигналов, причем критерием оптимальности характеристик таких фильтров является получение на выходе фильтра максимально возможного отношения пикового значения сигнала к среднеквадратическому значению помехи. Цель обработки при этом состоит не в воспроизведении формы сигнала, которая считается известной, а в наиболее надежной фиксации лишь факта наличия или отсутствия сигнала в принятом колебании.

Найдем выражение для комплексной частотной характеристики оптимального фильтра [5]. Пусть на вход линейного фильтра с комплексной частотной характеристикой K(j) воздействует сумма полностью известного сигнала s(t) и помехи n(t), представляющей собой стационарный в широком смысле случайный процесс с известной спектральной плотностью S_n() [4]:

x(t) = s(t) + n(t) , 0 £ t £ T .

Обозначим полезный сигнал и помеху на выходе фильтра через s_в(t) и n_в(t). Известно, что если на вход линейной системы с комплексной частотной характеристикой K(j) воздействует сигнал s(t), имеющий комплексный амплитудный спектр

,

то комплексный спектр сигнала на выходе системы определяется произведением Ф(j)K(j), а сам выходной сигнал – выражением

. (1.1)

Спектральная плотность помехи на выходе фильтра определяется выражением S_n(w)|K(jw)|², а ее дисперсия

. (1.2)

На основании формул (1.1) и (1.2) получаем выражение для отношения сигнал / помеха по мощности на выходе фильтра в некоторый момент времени t₀ :

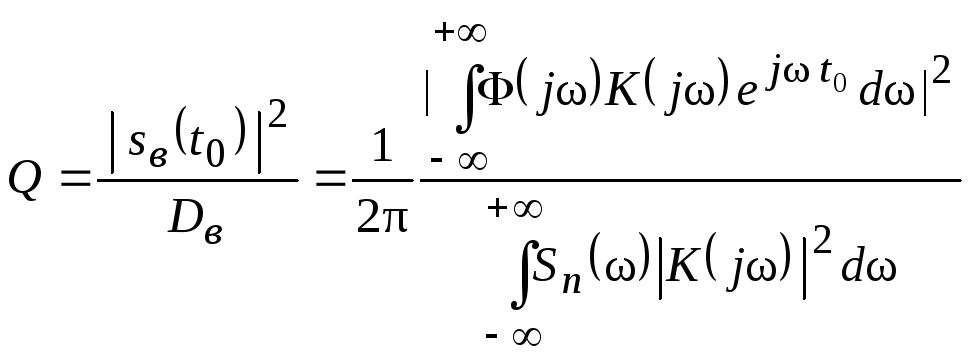. (1.3)

Необходимо найти такую функцию K(jw), при которой выражение (1.3) в некоторый момент времени t₀ достигает максимума. Одним из путей решения этой задачи является использование неравенства Шварца-Буняковского. Известно, что для двух произвольных комплексных функций f(x) и g(x) выполняется соотношение

, (1.4)

причем знак равенства имеет место только в случае, когда g(x) = c₀ f(x), где c₀ – постоянная; f*(x) – функция, комплексно-сопряженная f(x).

Запишем выражение (1.4), перейдя к переменной , в виде

.

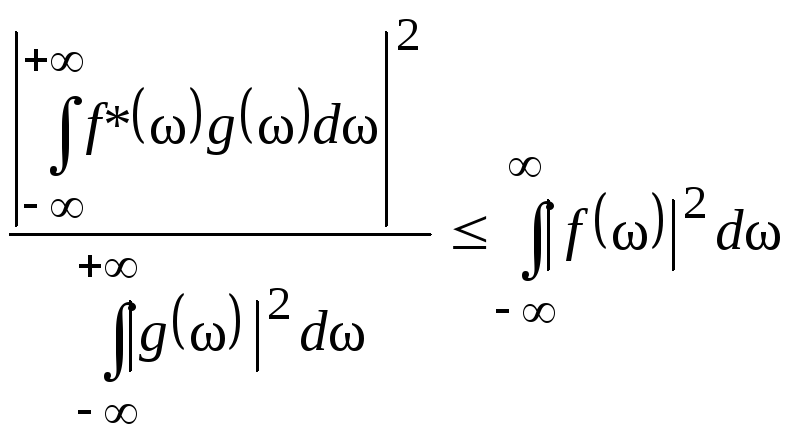Полагая здесь

(1.5)

получаем

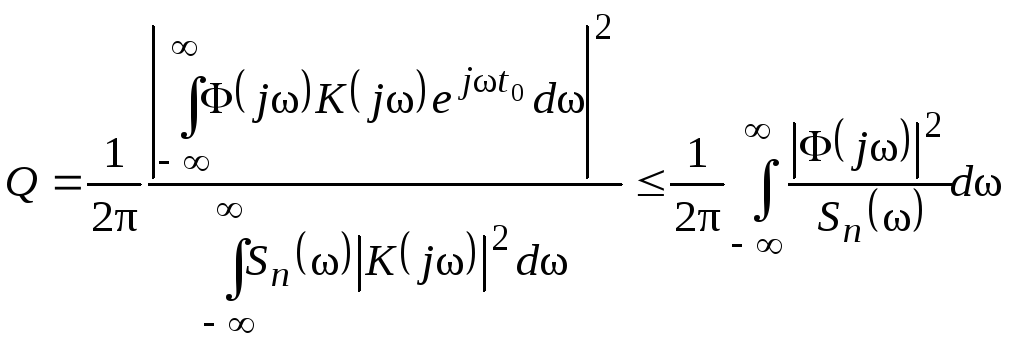(1.6)

Отсюда следует, что максимально возможное значение отношения сигнал / помеха

(1.7)

Согласно соотношению (1.5), это значение достигается лишь при выполнении условия

,

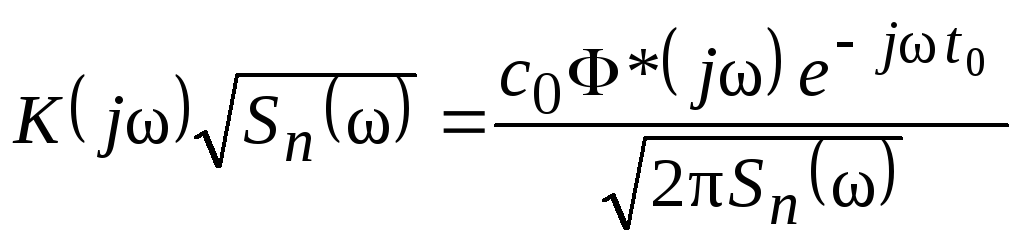или

(1.8)

где c – некоторая постоянная; t₀ – момент времени, соответствующий наибольшему значению отношения сигнал/помеха на выходе фильтра. Таким образом, комплексная частотная характеристика оптимального линейного фильтра определяется формулой (1.8), а наибольшее отношение сигнал помеха – выражением (1.7). Варьируя спектры сигнала Ф(jw) и помехи S_n(w) в формуле (1.7), можно при некоторых дополнительных условиях (например, постоянство энергии или мощности сигнала и др.), налагаемых на систему, найти наилучшую форму спектра сигнала (при которой максимизируется Q ) и наихудшую спектральную плотность помехи (при которой Q минимизируется).

В некоторых устройствах, например служащих для определения момента появления импульса, применяются фильтры, которые должны обеспечивать получение максимально возможного отношения крутизны сигнала к среднеквадратическому значению помехи. Такие фильтры можно назвать оптимальными по крутизне сигнала. Для определения комплексной частотной характеристики такого фильтра вместо самого сигнала s(t) надо рассматривать его производную по времени . При этом комплексная частотная характеристика фильтра, оптимального по крутизне сигнала, определяется выражением

,

где Ф₁^*(j) – комплексно-сопряженное значение спектра производной входного сигнала; с₁ – некоторая постоянная. Максимально возможное отношение крутизны сигнала к среднеквадратическому значению помехи будет

.

Используя известное соотношение для преобразования Фурье производной сигнала:

,

можно записать:

.

Тогда

,

.