В формулах (5) величина n число шагов, задается перед началом вычислений. При k = n процесс вычислений заканчивается.

Теорема 3. Для задачи А метод n является единственным оптимальным последовательным методом на классе Q унимодальных функций. Наилучшая гарантированная точность множества последовательных методов Pn на классе Q равна

= b a .

Fn+2

Следствие. Кол-во необходимых при решении задачи А вычислений значений ф-и f(x) 2 Q гарантирующих погрешность6 " равно числу n, удовлетворяющему неравенствам

7Метод ломаных

Предназначен для решения задач минимизации 1-ого и 2-ого типа для функций не являющихся унимодальными. Рассмотрим данный метод для класса функций, удовлетворяющих условию Липшица на отрезке и запишем определение. Говорят, что ф-я удовлетворяет условию Липшица на отрезке [a; b], если существует постоянная L > 0 такая, что

jf(x) f(v)j 6 L jx vj 8x; v 2 [a; b] (1)

Постоянную L называют константой Липшица. Геометрический смысл условия (1) следующий: угловой коэффициент

jf(x) f(v)j 6 L jx vj

для всех точек из [a; b]

7.1Описание метода ломаных

Пусть ф-я f(x) удовлетворяет условию 1 на отрезке [a; b]. Зафиксируем какую-либо точку v 2 [a; b] и определим ф-ю

g(x; v) = f(v) L jx vj

переменной x, причем a 6 x 6 b. g(x; v) кусочно-линейна на [a; b], график ее представляет собой ломаную линию, составленную из отрезков двух прямых, имеющие угловые коэффициенты L и пересекающихся в точке (v; f(v)). Кроме того в силу условия (1) выполняется неравенство:

f(x) g(x; v) > (L jf(x) f(v)j) jx vj > 0 (2)

jx vj

Покажем истинность левой части неравенства (2):

f(x) g(x; v) = f(x) f(v) + L jx vj

Запишем левую часть (2) в виде

f(x) f(v) + Ljx vj > (L jf(x) f(v)j)jx vj

jx vj

Отсюда следует, что

f(x) f(v) > jf(x) f(v)jjx vj

jx vj

т.е.

f(x) f(v) > jf(x) f(v)j

что выполняется всегда. Истинность левой части неравенства (2) доказана. Тогда из неравенства (2) следует, что

g(x; v) = f(v) Ljx vj 6 f(x) (3)

при всех x 2 [a; b]. Причем

13

g(v; v) = f(v)

Значит, график ф-и f(x) лежит выше графика ломанной g(x; v) при всех x 2 [a; b] и имеет с ней общую точку (v; f(v)).

Применение метода ломаных начинается с выбора произвольной точки x0 2 [a; b] и составления ф-и

g(x; x0) = f(x0) L jx x0j = p0(x)

Следующая точка x1 определяется из условия

p0(x1) = min p0(x)

x2[a;b]

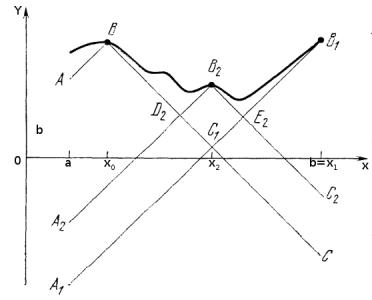
ABC график p0(x) = g(x; x0). С самая нижняя точка.

A1B1 график g(x; x1)

ABС1B1 график следующей ф-и p1(x) A2B2C2 график ф-и g(x; x2)

ABD2B2E2B1 график ф-и p2(x) Очевидно, что следующая точка

x1 = a

или

x1 = b

Берется новая ф-я

p1(x) = max[g(x; x1); p0(x)]

и находится очередная точка x2 из условия

p1(x2) = min p1(x) x2 2 [a; b] и т. д.

x2[a;b]

Пусть точки x1; x2; :::; xn n > 1, составляется ф-я

pn(x) = max[g(x; xn); pn 1(x)] = max g(x; xi) i > 0

Следующая точка xn+1 определяется из условия

pn(xn+1) = min pn(x) xn+1 2 [a; b] (4)

x2[a;b]

Если min pn(x) достигается в нескольких точках, то в качестве xn+1 можно взять любую из них.

x2[a;b]

14

7.2Сходимость метода ломаных

Сходимость устанавливается следующей теоремой.

Теорема 4. Пусть f(x) произвольная ф-я, удовлетворяющая на отрезке [a; b] условию (1). Тогда последовательность fxng полученная с помощью метода ломаных такова, что

причем справедлива оценка

06 f(xn+1) f 6 f(xn+1) pn(xn+1) (5)

последовательность fxng сходится к множеству X точек минимума ф-и f(x) на [a; b] т. е.

lim (X ; xn) = 0

n!1

7.3Определение константы L

При определении константы L может быть полезна следующая теорема.

Теорема 5. Пусть ф-я f(x) дифференцируема на отрезке [a; b] и ее производная f0(x) ограничена на этом отрезке. Тогда f(x) удовлетворяет условию (1) с константой

L = sup jf0(x)j

x2[a;b]

Док-во. По формуле конечных приращений (по ф. Тейлора) для 8x; v 2 [a; b] имеем

f(x) f(v) = f0(v + (x v))(x v)

где 0 < < 1. Отсюда из-за ограниченности производной f0(x) следует утверждение теоремы.

7.4Достоинства и недостатки метода ломаных

Достоинства:

Метод сходится при любом выборе начальной точки

Метод близок к оптимальным методам на классе ф-ий, удовлетворяющих условию (1). Недостатки:

С увеличением числа шагов n растет объем памяти компьютера для хранения координат вершин ломаной pn(x)

Метод невозможно реализовать без знания константы L

7.5Алгоритм метода ломаных при выборе начальной точки x0 = a

1. Выделим в кач-ве начальной точки левую границу интервала - a, тогда следующая точка будет

15

x0 = b

а следующая точка x1 и параметр p1 определяются из системы уравнений

(

(x1 a)L + p1 = f(a) (b x1)L + p1 = f(b)

Решив эту систему уравнений получим

x1 = 21L (f(a) f(b) + L (a + b))

p1 = 12 (f(x1) + p1)

1 = 21L (f(x1) p1)

3.Из полученных двух пар (x01; p1) и (x001 ; p1) выбираем ту, у которой вторая компонента минимальна (в данном случае любую пару). Обозначим (x01; p1) как (x2; p2) и исключим из рассматриваемого множества точек

4.Вместо пары (x2; p2) добавляем две новые пары (x02; p2) и (x002 ; p2), компоненты которых находятся по формулам

x02 = x2 2

x002 = x2 + 2

p2 = 12 (f(x2) + p2)

2 = 21L (f(x2) p2)

5.Произвольный n-ый шаг. Из n полученных на предыдущих шагах пар выбираем ту, у которой вторая

компонента минимальна. Обозначим ее (xn; pn). Исключаем эту пару из рассматриваемого множества и добавляем вместо нее две новые пары чисел (x0n; pn) и (x00n; pn), где

pn = 12 (f(xn) + pn) n = 21L (f(xn) pn) (7)

6. Полагая

v = xn f = f(xn)

получим приближенное решение задачи минимизации. Погрешность определения равна

jf(v ) f j 6 2L n (8)

16

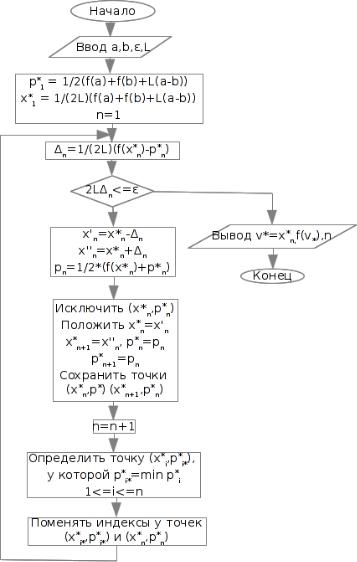
7.6Блок-схема метода ломаных

Входные параметры: a; b; L; " Выходные параметры: v ; f(v ); n

8Метод равномерного пассивного перебора для минимизации неунимодальных ф-ий L

Обозначим Q(L) класс функций удовлетворяющих условию Липшица (1) с одной и той же для всех функций этого класса константой L > 0. Для функций f(x) принадлежащих этому классу будем рассматривать задачу минимизации первого типа, когда ищется величина, равная точной нижней границе функции f(x) x 2 [a; b]. Для решения этой задачи будем пользоваться методами, которые заключаются в выборе точек x1; x2; :::; xn таких, что a 6 x1 6 x2 6 ::: 6 xn. Вычисляем значения функции f(x1); f(x2); :::; f(xn) и определяем

f(xk) = min f(xi)

16i6n

принимаемый за приближение f .

Как выбрать число n и точки x1; x2; :::; xn чтобы точная верхняя граница была

sup ( min f(xi) f ) 6 " (9)

f2Q(L) 16i6n

Простейшим методом для решения задачи (9) является следующий метод равномерного перебора, когда точки x1; x2; :::; xn выбираются по правилу (10)

17

x1 = a + h2

x2 = x1 + h

...

xi = xi 1 + h

xi+1 = xi + h

или

xi+1 = x1 + ih

...

xn 1 = x1 + (n 2)h xn = min(x1(n 1)h; b)

где

h 6 2L"

шаг метода.

18