Экзаменационные вопросы

1.Необходимые и достаточные условия локального экстремума ф-и одной переменной. Классический метод нахождения экстремумов.

2.Отыскание экстремума ф-и одной переменной методом деления отрезка пополам.

3.Отыскание экстремума ф-и одной переменной методом золотого сечения.

4.Отыскание экстремума ф-и одной переменной методом Фибоначчи.

5.Отыскание экстремумов ф-и одной переменной методом ломанных.

6.Симметричные методы. Постановка задачи об оптимальных методах.

7.Функции многих переменных: линейные пространства. Постановка задачи минимизации.

8.Необходимые и достаточные условия локального экстремума ф-и многих переменных.

9.Отыскание безусловного экстремума ф-и многих переменных градиентным методом (с дроблением шага и методом наискорешего спуска.

10.Отыскание безусловного экстремума ф-и многих переменных методом покоординантного спуска.

11.Необходимые условия локального экстремума ф-и многих переменных при ограничениях-равенствах: метод множителей Лагранжа.

12.Достаточные условия локального экстремума ф-и многих переменных при ограничениях-равенствах: метод множителей Лагранжа.

13.Обобщенная ф-я Лагранжа. Единственность вектора Лагранжа для нормального оптимального пла- на.

14.Общая задача математического программирования.

15.Выпуклые множества (и их свойства) и выпуклые ф-и.

16.Необходимые и достаточные условия минимума выпуклых ф-и на выпуклых множествах.

17.Теорема Куна-Таккера.

18.Отыскание условного экстремума ф-и многих переменных методом покоординантого спуска.

19.Отыскание условного экстремума ф-и многих переменных методом проекции градиента.

20.Проекция точки на выпуклое множество n-мерного пространства.

21.Проекция точки на гиперплоскость.

22.Проекция точки на аффинное множество.

23.Проекция точки на шар и на замкнутое полупространство.

24.Отыскание условного экстремума ф-и многих переменных методом штрафных функций.

25.Ф-и внешних штрафов для множества, определяемого ограничениями-равенствами и ограниченияминеравенствами.

26.Отыскание условного экстремума ф-и многих переменных методом барьерных ф-ий.

27.Общая задача ЛП. Стандартная форма задачи ЛП. Различные формы записи задачи ЛП.

28.Симплексный метод: построение опорных планов.

29.Условия оптимальности опорного плана.

30.Алгоритм симплексного метода. Симплексная таблица.

31.Решение задачи ЛП методом больших штрафов и двухэтапным методом.

32.Понятие функционала. Вариация и ее свойства.

x1

33. Уравнение Эйлера. Задача с неподвижными границами для функционала F (x; y; y0)dx

x0

1

Список литературы

1.Аттенков А.В., Галкин С.В., Зарубин В.С. “Методы оптимизации” 2003 г.

2.Васильев Ф.П. “Численные методы решения экстремальных задач”

3.Сухарев А.Г., Тимохов А.В., Федоров В.В. “Курс методов оптимизации” изд. Науки 1986 г.

4.“Математическое программирование”

5.Дифференциальные уравнения и вариационное исчисление” изд. Наука

6.Гловацкая А.П. “Методы и алгоритмы вычислительной математики” изд. Радио и Связь 1999 г.

Часть I

Методы минимизации ф-и одной переменной

1Постановка задачи. Локальные и глобальные экстремумы

Пусть

R1 = fx : 1 < x < +1g

X некоторое множество из R1(числовая ось). f(x) ф-я определенная на множестве X и принимающиая во всех точках X конечные значения. Для строгой поставки задачи минимизации потребуются следующие определения математического анализа:

Определение 1. Точку x принадлежащую X называют точкой глобального минимума функции f(x) на X, если f(x ) 6 f(x) для всех x 2 X. Величину f(x ) называют наименьшим или минимальным

значением функции f(x) на множестве X и обозначают как min = f(x )

x2X

Множество всех точек глобального минимума функии f(x) на X будем обозначать как X . Пример 1. Пусть задана ф-я и множество X

f(x) = sin2( x ) X = fx : 1 6 x 6 2g

Тогда минимальное значение f(x) равно 0 и множество X состоит из одной точки x = 1.

Пусть X = x : 13 6 x 6 1 , тогда X = 13 ; 12 ; 1 .

Пусть X = fx : 2 6 x < +1g, тогда f(x) не имеет на данном множестве наименьшего значения и

X = .

Определение 2. Функция f(x) называется ограниченной на множестве X снизу, если существует число M такое, что f(x)> M для всех x 2 X. Ф-я f(x) не ограниченна снизу на X, если существует

последовательность точек fxkg 2 X для которой lim f(xk) = 1.

k!1

Определение 3. Пусть f(x) ограниченна снизу на X, тогда число f называется точной нижней гранью функции f(x) на множестве X, если

f 6 f(x) для всех x 2 X

для любого сколь угодного малого " > 0 найдется точка x 2 X для которой f(x") < f + "

Если ф-я f(x) не ограниченна снизу на множестве X, то в кач-ве точной нижней грани функции f(x) на X принимают f = 1

Нижнюю грань ф-и f(x) на множестве X обозначают как

f = inf f(x)

x2X

Точная нижняя грань существует всегда, минимум нет. Пример.

f(x) = x2 0 < x 6 1

на этом множестве минимума у функции нет, а точная грань есть, хоть и не входит в это множество

inf f(x) = 0

x2X

2

Определение 4. Последовательность fxkg 2 X называется минимизирующей для f(x) на X , если

lim f(xk) = inf f(x) = f

k!1 x2X

Минимизирующая последовательность существует всегда.

Определение 5. Последовательность fxkg 2 X называется сходящейся к непустому множеству X, если

lim (xk; X) = 0

k!1

где расстояние от xk до X.

Существует два типа задач минимизации ф-и f(x) на множестве X.

1.Задачи, в которых требуется определить точную нижнюю грань, для этих задач не важно будет ли множество X точек минимума функции f(x) непустым или же оно будет пустым.

2.Задачи, у которых множество X обязательно не пусто и требуется наряду с точной нижней гранью f найти какую-либо точку x 2 X

Оба типа задач решаются путем построения минимизирующих последовательностей. Но построение минимизирующих последовательностей сходящихся к множеству X в общем случае требует привлечения специальных методов. Будем рассматривать лишь такие задачи второго типа, у которых любая минимизирующая последовательность сходится к множеству X . Класс таких задач определяется теоремой Вейерштрасса.

Теорема Вейерштрасса. Пусть X закнутое числовое множество на прямой R1, ф-я f(x) непрерывна на X, тогда f(x) ограниченна снизу на множестве X, а множество X точек минимума ф-и f(x) на X непусто, замкнуто и любая минимизирующая последовательность сходится к множеству X . (Без док-ва).

Для задач второго типа можно находить также точки локального минимума.

Определение 6. Точка v называется точкой локального минимума ф-и f(x) на множестве X, со

T

значением f(v ), если существует число > 0 такое, что f(v ) 6 f(x) для всех x 2 X fx : jx v j < g = O (v ), где O (v ) - альфа-окрестность точки v .

Если при некотором равенство f(v ) = f(x) для x 2 O (v ) возможно только при x = v то v - точка строгого локального минимума.

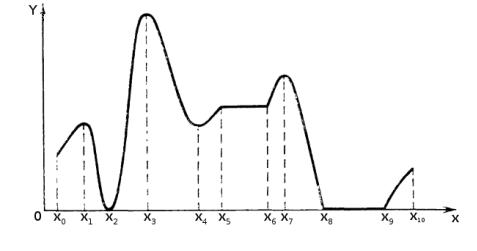
На рисунке точки x0; x2; x4 точки строгого локального минимума. В точках x5 6 x 6 x6 x8 6 x 6 x9 имеет место нестрогий локальный минимум.

Точки локального минимума в которых минимум достигается в смысле определения 1 называются точками глобального или абсолютного минимума функции f(x) на множестве X. Если ф-я f(x) унимодальна, то у ней все точки локального минимума являются точками глобального минимума.

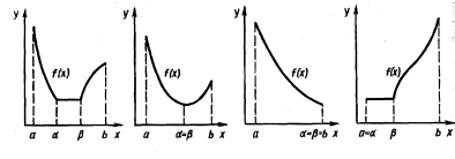
Определение 7. Функцию f(x) называют унимодальной на отрезке [a; b] если она непрерывна на [a; b]

исуществуют числа ; такие, что a 6 6 6 b такие, что

f(x) строго монотонно убывает при a 6 x 6 a <

f(x) строго монотонно возрастает, если 6 x 6 b < b

3

f(x) = f = inf f(x) X 2 [a; b] 6 x 6 ,

x2X

Если = , то f(x) строго унимодальная на [a; b]

2Задача максимизации функции

Определение 8. Ф-я f(x) называется:

ограниченной сверху на множестве X, если существует число , такое, что f(x) 6 x 2 X

Неограниченной сверху на X, если существует последовательность fxkg 2 X для которой

lim f(xk) = +1

k!1

Ф-ю f(x) называют ограниченной на X, если она ограниченна на X снизу и сверху.

Определение 9. Если ф-я f(x) ограничена сверху на X, то f называется точной верхней гранью ф-ю f(x) на множестве X в том случае, когда

f(x) 6 f x 2 X

для любого сколь угодного малого " > 0 найдется точка x 2 X для которой f(x") > f "

Если f(x) неограниченна сверху на X, то f = +1 Последовательность fxkg 2 X называется максимизирующей, если

lim f(xk) =f

k!1

Если существует точка x 2 X такая, что

f(x ) = f

то ее называют точкой глобального максимума f(x) на множестве X. А величину f наибольшим или максимальным значением на том же множестве X или глобальным максимумом. Множество точек максимума f(x) на X обозначают через X а верхню грань как

f = supf(x).

x2X

В задачах максимизации различают задачи двух типов:

ищется f

ищется f и какая-либо точка x 2 X .

Для точных границ всегда выполняется следующее равенство

supf(x) = inf ( f(x))

x2X x2X

Это означает что любая задача максимизации ф-и f(x) на множестве X равносильна задаче минимизации ф-и f(x) на том же самом множестве X.

Определение 10. Точка v принадлежащая множеству X называется точкой локального максимума, если существует число > 0 такое, что f(v ) > f(x) для всех x 2 X Tfx : jx v j < g для x 2 O (v ).

Если при некотором > 0 равенство f(v ) = f(x) для x принадлежащей этой окрестности возможно только при x = v , то v - точка строгого локального максимума.

4