3Необходимые и достаточные условия локального экстремума. Классический метод нахождения экстремумов функций

Необходимое условие локального экстремума определяется следующей теоремой.

Теорема Ферма. Пусть ф-я f(x) определена в некотором интервале X и во внутренней точке v этого интервала принимает наибольшее (наименьшее) значение. Если существует двустороняя конечная производная f0(v) в этой точке, то необходимо что

f0(v) = 0

Определение. Точки в которых f0(x) = 0 принято называть стационарными. Достаточные условия локального экстремума:

в первой форме. Для испытания стационарной точки v подставляют в производную f0(x) сначала x < v, а затем x > v и устанавливают знак производной вблизи от точки v слева и справа от нее.

Если при этом производная меняет знак плюс на минус, то имеет место локальный максимум, если же минус на плюс, то имеет место локальный минимум. Если же производная f0(x) знака не меняет, то экстремума нет (точка перегиба (одна переменная) или седловая).

во второй форме. Для испытания стационарной точки v подставляют значение второй производной. Если f"(v) > 0 локальный минимум, иначе локальный максимум.

3.1Классический метод

Пусть f(x) кусочно-непрерывная на [a; b]. Тогда точками экстремума ф-и f(x) на [a; b] могут быть лишь те точки в которых выполняется одно из следующих условий.

f(x) терпит разрыв

либо f(x) непрерывна, но производная f0(x) не существует

либо производная f0(x) существует и равна 0

либо x = a, либо x = b (экстремум на границе). Такие точки точки, подозрительные на экстремум.

Чтобы найти глобальный минимум (максимум) ф-и f(x) на интервале [a; b] нужно перебрать все точки подозрительные на экстремум на этом интервале. И среди них выбрать точку с наименьшим (наибольшим) значением. Если вместо отрезка [a; b] дано множество

X = fx : a 6 x 6 +1g

или

X = fx : b > x > 1g

или

x = R1 (вся числовая прямая)

то дополнительно нужно изучить поведение ф-и при x стремящемся к +1 и 1.

Классический метод используется в тех случаях, когда достаточно просто удается выявить подозрительные на экстремум точки. Однако это возможно далеко не всегда. Часто не удается вычислить производную f0(x) либо решения у-ния f0(x) = 0 связано со значительными трудностями. В этом случае для нахождения экстремумов ф-и используют численные методы.

4Метод деления отрезка пополам

Пусть минимизируемая ф-я f(x) унимодальна на отрезке [a; b]. Поиск начинается с выбора двух точек

постоянная величина, называемая параметром метода. После выбора точек x1 и x2 вычисляют значения f(x1) и f(x2), и сравнивают их между собой.

Если

5

f(x1) 6 f(x2)

то полагают

a1 = a b1 = x2

Если

f(x1) > f(x2)

то полагают

a1 = x1b1 = b

Так как f(x) унимодальна на [a; b], то получившийся отрезок [a1; b1] имеет общую точку со множеством X на интервале [a; b] и его длина

b1 a1 = b a +

2

Пусть отрезок [ak 1; bk 1] имеющий непустое пересечение уже известен. Его длина

и вычисляем f(x2k 1) f(x2k). Сравниваем их, если

f(x2k 1) 6 f(x2k)

то полагаем

ak = ak 1 bk = x2k.

Если же

f(x2k 1) > f(x2k)

то полагаем

ak = x2k 1 bk = bk 1.

Длина получившегося отрезка равна

bk ak = b 2ak +

в этом же отрезке [ak; bk] имеет пересечение с X (с множеством точек минимума) непустое множество. Если кол-во вычислений значений ф-и ничем не ограничено, то процесс деления отрезка пополам продолжают до тех пор, пока не получат отрезок [ak; bk] длины bk ak < " заданная погрешность (точность) (" > ). После определения отрезка [ak; bk] в кач-ве приближения к точке локального минимума можно

взять точку

xn = x2k 1

при

f(x2k 1) 6 f(x2k)

и точку

xn = x2k

при

f(x2k 1) > f(x2k)

6

а значение f(xn) может служить приближением

f = inf f(x)

x2[a;b]

При этом будет допущена погрешность

jxn j 6 max(bk xn; xn ak) = b 2ak .

Примечание. Если находится локальный максимум f(x), то точки x1иx2 определяются так же, а границы сужаются по иному.

Если

f(x1) > f(x2)

то

a1 = a b1 = x2

Если

f(x1) < f(x2)

то

a1 = x1b1 = b.

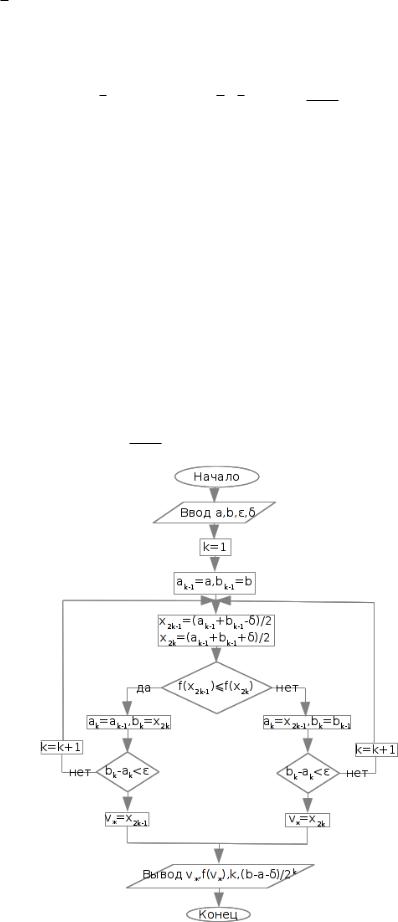
4.1Блок-схема метода деления отрезка пополам

Входные параметры: a; b; ";

Выходные параметры: v ; f(v ); k; b ak

2

7