0b1 1
Bb2 C
b = B C @::: A
bm
заданный вектор пространства Em
называется аффинным множеством или линейном многообразием. Всякое аффинное множество выпукло. Пусть в (4:10 )
bi = const i = 1; :::; m
а векторы ai - линейно-независимы и m < n (если m = n, то множество X будет состоять из одной точки). Проекцию точки u на множество X будем искать в виде
m
P
! = u + jaj (4:11)
j=1
Из требования ! 2 X получим систему линейных алгебраических у-ний
m
P j < ai; aj >= bi < ai; u > i = 1; 2; ::: (4:12)
j=1
для определения коэффициентов 1; :::; m. Определителем этой системы является определитель Грама, который для линейно-независимых a1; :::; amбудет отличным от нуля.
Определение. Определителем Грама системы векторов a1; :::; am называется
< a2 |
; a1 |
> |
< a2 |
; a2 |
> |
::: |
< a2 |
; am |
> |
|||||||
|
< a1 |
; a1 |
> |
< a1 |
; a2 |
> |
::: |
< a1 |
; am |
> |
|
|||||
< a |
m |
; a |
> |
< a |
|
; a |
> |
::: |
< a |
|
; a |
m |
> |
|||
|
|
1 |
|
m |
2 |
|
::: |
m |
|
|
|
|||||
|
|
::: |
|
::: |
|
|
::: |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Он в точности равен объему n-мерного параллелепипеда, построенного на векторах a1; :::; am. Поэтому искомые коэффициенты 1; :::; mсуществуют и однозначно определяется из системы (4:12). Для точки
m |
m |
m |
m |
m |
m |
< ! u; x ! >= j=1 j < aj; x u > i=1 i(j=1 j < ai; aj >) = j=1 jbj j=1 j < aj; u > |
=1 i(bi < |
||||
P |
P |
P |
P |
P |
iP |
ai; u >) = 0 (4:14)
для всех точек x 2 X Здесь выражение
m
P
j < ai; aj >
j=1
преобразовано в соотвествие с (4:12)
Следовательно, по теореме 1 найденная точка ! будет проекцией точки u на множество X. В координатной форме выражение (4:11) записывается следующим образом
n
P
!s = us + jajs s = 1; 2; :::n (4:15)
j=1
где ajs- s-тая координата вектора aj
21.5Проекция точки на шар
Пусть
X = S(x0; R) = fx 2 En : jx x0j 6 Rg
шар радиусом R с центром в точке x0.
Из геометрических соображений следует, что проекцией точки u 2= X является точка
! = x0 + R(u x0) (4:16)
ju x0j
Для строгого док-ва этого утверждения достаточно проверить выполнение неравенства (4:4). Получим,
39
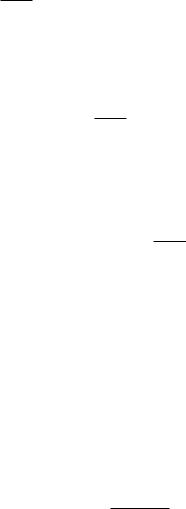
< ! u; x ! >=< |
R(u x0) |
(u |
x0); (x x0) |
R(u x0) |
>= ( |
|
R |
|
|
1) < u x0; (x x0) R |
(u x0) |
>= |
||||||||||||||
u |
|
x0 |
j |
u |
|
x0 |
j |
u |
|
x0 |
j |
u |
|
x0 |
j |
|||||||||||
|
j |
|
|
R |
|
j |
|
|
j |
|
|
|
2 |
|
j |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ju x0j |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
( |
ju x0j |
1)(< u x0; x x0 > R |
ju x0j |
) |
|
|
|
|
|
||||||||||||
(ju Rx0j 1)(< u x0; x x0 > Rju x0j) > 0
Последнее неравенство следует из того, что
ju x0j > R
то есть
R |
1 < 0 |
ju x0j |
Кроме того
<u x0; x x0 >= ju x0jjx x0j cos 6 ju x0jjx x0j 6 Rju x0j
Вкоординатной форме (4:16) запишется так
!j = xj |
+ R |
uj x0j |
0 |
|
ju x0j |
|
|
21.6Проекция точки на замкнутое полупространство
Пусть
X = fx 2 En :< c; x >6 g
замкнутое полупространство, определяемое гиперплоскостью
< c; x >=
Пусть точка u 2= X т.е.
< c; u >>
Как и в случае с гиперплоскостью представим проекцию точки u на множество X в виде
|
|
|
|
|
|
<c;u>)c |
|
|
|||
|
|
|
! = u + |
( jcj2 |
|
(4:17) |
|
||||
Проверим, является ли точка ! проекцией точки u на X. Получим |
|||||||||||
< ! u; x ! >=< |
( <c;u>)c |
; x u |
( <c;u>)c |
>= |
( <c;u>) |
(< c; x > < c; u > + < c; u >) = |
|||||
jcj2 |
|
jcj2 |
|
|
|
jcj2 |
|||||
|
|
|
( <c;u>) |
(< c; x > ) > 0 (4:18) |
|||||||
|
|
|
jcj2 |
|
|||||||
при x 2 X. Следовательно, точка ! есть искомая проекция. В координатной форме выражение (4:17) имеет вид (4:10)
21.7Проекция точки на n-мерный параллелепипед
Пусть
X = fx = (x1; :::; xn) 2 En : i 6 xi 6 i; i = 1; 2; :::; ng
где i; i : i < i - заданные числа. Пусть u 2= X. Положим
0!11
B!2C
! = B C @ ::: A
!n
где координаты равны
40