
21869_4f7d312f91bac43d4530a115cb0453bf
.pdf
Наглядную модель растянутой пружины можно распространить на любые деформируемые упругие твердые тела.
3. Поле гравитации F = G M m /r2.
|
|
d r e = d r |
|
|
F = F e ′ |
r |
|
|
|
|
|
|
|
0 |
e |
r |
e ′ |
|
||
r r
A = ∫ Fdr = e e′∫(GM m/r2)dr = GM m/r U = - GM m/r .
∞∞
На бесконечности потенциальная энергия принимается равной нулю. При этом на бесконечности (относительно большом расстоянии) по отношению к силовому притягивающему центру она максимальна. Следовательно, при любом другом положении она меньше, чем ноль, то есть отрицательна.
Закон сохранения полной механической энергии.
Рассмотрим поле центральных сил (пусть силовой центр для определенности будет притягивающим).
Будучи предоставлено самому себе ранее, и оказавшись в разное время последовательно в двух произвольных точках (1), а затем (2), тело должно иметь
|
|
|
|
|
|
|
|
|
|
как кинетическую, |
|
|
|
|
|
|
|
|
|
|
|
так |
и |
|
|
|
|
|
|
|
|
|
|
потенциальную |
|
|
|
|
F 2 |
( 2 ) |
F 1 ( 1 ) |
|
|
энергии |
по |
||
|
|
|
|
|
отношению |
к |
|||||
н еки й |
|
ц ен тр |
|
|
|
|
си лов ая |
||||
|
2 |
2 |
|
данному |
|||||||
|
|
|
|
ли н и я |
|
||||||
|
|
|
|
T 2 v 2 |
T 1 v 1 |
притягивающему |
|||||
|
|
|
|
U 2 r 2 |
U 1 r 1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
(либо |
к |
отталкивающему) центру. Тогда:
41

A12 = T2 - T1, v2>v1 и A12 = U1(r1) - U2(r2), (r2<r1)
Работа по перемещению тела в силовом поле определена двумя способами: как разность кинетических энергий и как разность потенциальных энергий тела, но так, чтобы знак работы оставался одинаковым. Приравняем правые части
T2 - T1 = U1 - U2 T2 + U2 = T1 + U1 = ...
Такие суммы справедливы для произвольных координат (а в данном случае и точек траектории) по отношению к центру как началу координат, следовательно
T + U = CST = E
Таким образом, сумма кинетической и потенциальной энергий является сохраняющейся величиной частицы (системы частиц, тел) при выполнении условия замкнутости и в центральном (консервативном) силовом поле. Таков важнейший закон физики - закон сохранения энергии.
Заметим, что в более широком смысле полная энергия во вселенной есть по нашим представлениям постоянная величина.
§ 9 Связь силы и потенциальной энергии (в поле консервативных сил)
Как сила так и энергия - обе являются функциями координат в полях центральных сил F = F ( r ), U = U ( r ). Имеем
dA = Fdr = Fx dx + Fy dy + Fz dz = - dU,
при этом потенциальная энергия, U, является скаляром, зависящим в общем случае от всех трех координат x, y, и z. Произведения компонентов векторов обозначим в виде
42
Fx dx = -dU|y, z = cst, Fy dy = -dU|x, z = cst, Fz = -dU|x, y = cst,
тогда компоненты силы представляют собой производные вида
Fx = - ∂U/∂x, Fy = -∂U/∂y, Fz = -∂U/∂z.
Здесь вычисляются производные только по одной из трех переменных, так называемые частные производные, две другие переменные считаются константами как параметры. С помощью этих компонентов можно записать вектор силы
F= Fxi + Fyj + Fzk = -((∂U/∂x) i + (∂U/∂y) j + (∂U/∂z) k) = -(∂/∂x) i + (∂/∂y) j +
+(∂/∂z) k)U, но ((∂/∂x)i + (∂/∂y)j + (∂/∂z)k) = , тогда в краткой записи имеем
F = - U ≡ - grad U.
Значок - набла, или аббревиатура grad - градиент означают, таким образом, сумму частных производных, помноженных на орты декартовой системы координат (градиент можно записать и в любой другой системе координат), а физически это означает направление максимального изменения функции, в данном случае потенциальной энергии U.
Заметим, что
dU = (∂U/∂x)dx + (∂U/∂y)dy + (∂U/∂z)dz
является полным дифференциалом потенциальной энергии. [∂U/∂x] = Дж/м=Н
Закон сохранения энергии и однородность времени
Покажем аналитически, как однородность времени приводит к закону сохранения энергии. С одной стороны имеем
A12 = T2 - T1, (*)
с другой стороны
43

A12 = ∫Fdr = -∫[(∂U/∂x)dx + (∂U/dy)dy + (∂U/∂z)dz] = -∫dU
Теперь пусть U* зависит и от времени, тогда
dU* = (∂U/∂x)dx + (∂U/∂y)dy + (∂U/∂z)dz + (∂U/∂t)dt.
Итого получили
A*12 = -(∫dU + ∫(∂U/∂t)dt).
В данном случае система находится в силовом поле других тел, которое меняется во времени. Работу А12 можно получить, если вычесть из полного дифференциала U* слагаемое зависящее от времени
A12 = - (∫dU* - ∫(∂U/∂t)dt).
Сопоставляем последнее выражение с выражением для работы через кинетические энергии (*)
T2 - T1 = U1* - U2* + ∫(∂U/∂t)dt (T2 + U2*) = (T1 + U1*) + ∫(∂U/∂t)dt
Очевидно, что для выполнения закона сохранения полной энергии необходимо равенство нулю последнего интеграла. Отличие его от нуля означало бы, что система предполагается незамкнутой. Наша система замкнутая (точнее квазизамкнутая) и протекание процессов в ней от времени не зависит, поэтому последнее слагаемое равно нулю.
Однородность времени означает следующее. Если замкнутую систему поставить в совершенно одинаковые условия в два произвольные моменты времени, то начиная с любого из этих двух моментов все явления в системе будут протекать совершенно одинаково. (Будет совершаться одинаковая работа, и сохраняться полная энергия).
44

Замечание: вопрос о том надо ли всю Вселенную считать замкнутой или не замкнутой системой, по-видимому, пока остается открытым. Части вселенной: Солнечную систему, Галактику можно считать в известном смысле квазизамкнутыми.
§ 10 Момент силы. Векторное произведение
Динамика = кинематика + масса, m F (появление массы приводит к появлению силы).
Наглядным примером понятия момента силы может служить следующая схема, в которой направление силы и плеча взаимно перпендикулярны.
F
l
M = l·F
F - сила, l - плечо, M - момент
Момент силы в общем случае - вектор (точнее псевдовектор). Для более полного определения момента силы (иногда говорят: «момент вращения» или «вращательный момент») математика предоставляет нам векторное произведение векторов.
M = r×F; |M| = r F Sinϕ
45
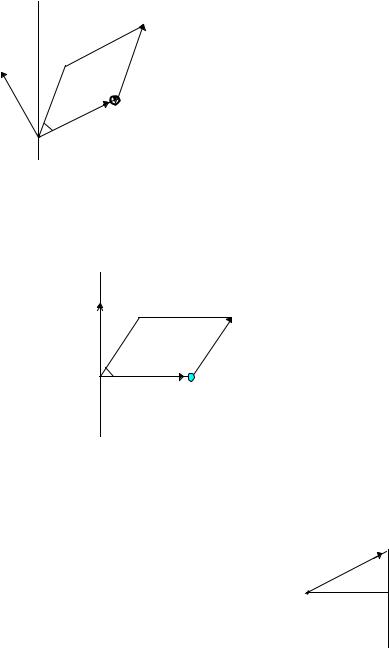
O′
|
|
F |
M |
|
|
|
ϕ |
r |
|
A |
|
Момент |
относительноточки |
|
|
О |
|
|
O′ |
|
M |
|
F |
|
ϕ |
|
r |
Момент |
относительнооси |
|
O |
r  M
M
OO′  ϕ
ϕ
Видсверху (относительнооси) 
F
46

Величина момента=площади параллелограмма
F
|
ϕ |
ϕ |
FSinϕ |
OO′ |
r |
Sпаоралл. = 2 (1/2)rFSinϕ
M всегда перпендикулярен плоскости, в которой лежит параллелограмм. М также как r и F вектор и как вектор записывается через компоненты и обладает всеми свойствами векторов
M = Mx i + My j + Mz k.
Овекторном произведении векторов
с= a×b
c плоскости, в которой находятся вектора a и b и его величина по определению равна
с = a b Sin (a^b)
причем, направление вектора с определяется по правилу правого винта, следовательно
a×b = - b×a
47
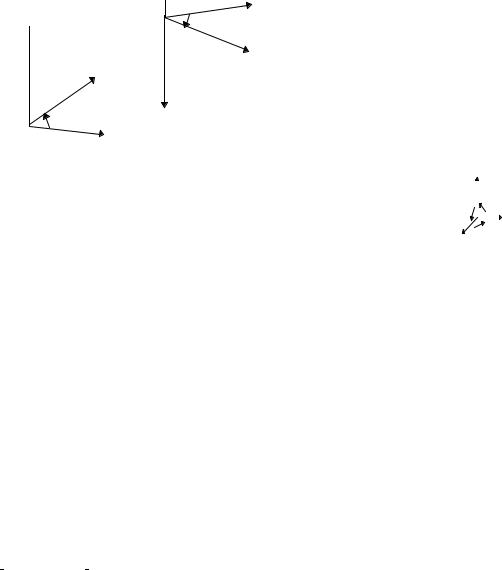
-c
c
b
a c
b 1. Свойство a×b = -b×a называется
aантикоммутативностью
2.Применим свойство антикоммутативности и определение величины для векторного перемножения ортов декартовой системы
координат, имеем
3.
|
a×b = c |
|
|
|
b×a = c = -a×b |
i×i = j×j = k×k = 0. |
|
|
|||
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На |
рисунке |
показано |
направление |
поворота |
|
|
|||||
положительного знака |
|
|
|
|
|
||||||
i×k =-j, i×j = k j×i =-k, j×k = i k×i = j, k×j =-i. |
|
|
|
||||||||
Тогда имеем для векторного произведения двух векторов |
|
|
|||||||||
a×b = (axi + ayj + azk)×(bx i + by j + bz k) = |
|
|
|
||||||||
= (ay bz - az by)i + (az bx - ax bz)j + (ax by - by ax)k |
|
|
|
||||||||
Второй |
способ |
нахождения |
|
результирующего вектора |
|
при векторном |
|||||
перемножении векторов заключается в составлении определителя вида |
|||||||||||
|
i |
j |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
a x |
a y |
a z |
|
|
|
|
|
|
|
|
|
b x |
b y |
b z |
|
|
|
|
|
|
|
|
Действуя по мнемоническому правилу можно получить компоненты вектора с как произведения двух других векторов a и b.
с = aхb = i (ay bz - az by) + j (az bx - ax bz) + k (ay bx - ax by)
cx |
cy |
cz |
48

Для момента импульса имеем
i j k
x y z
F x F y |
F z |
M = r×F = i (y Fz – z Fy) + j (z Fx – x Fz) + k (x Fy - y Fx).
Численно модуль момента силы M ( M2 = Mx2 + My2 + Mz2), или как иногда пишут вращательного момента, равен площади параллелограмма со сторонами r и F.
§ 11 Момент импульса. Закон сохранения момента импульса
По определению момент импульса равен (для одной частицы)
L = r×p = m r×v, L = r p Sin (r^p)
O′ |
v |
r
 m
m
O
Возьмем первую производную по времени от момента импульса
dL /dt = (dr/dt)×p + r×(dp/dt) = v×mv + r×F = (т.к. v×v =0 ) = M.
(Здесь вычисляется производная от произведения двух функций согласно правилу и с сохранением векторного произведения)
Получили равенство
49

dL/dt = M.
Налицо аналогия со вторым законом Ньютона (dp/dt = F). Таким образом, мы как бы обобщили, перенесли формулу второго закона Ньютона на произвольное вращательное движение.
Рассмотрим систему частиц. Тогда имеем по принципу суперпозиции для момента импульса и момента силы
L = ∑ Li и M = ∑ Mi
Возьмем первую производную по времени от момента импульса для системы частиц
dL/dt = ∑ Mi = ∑ ∑ Mlk + ∑ Mj
i |
l, k |
j |
Здесь моменты сил представлены в виде моментов внутренних и внешних. Индексами l, k обозначены моменты внутренних сил, а индексом j - моменты внешних сил. Согласно третьему закону Ньютона сумма моментов внутренних сил должна быть равна нулю так как M lk = - M kl и тогда
dL/dt = M внешн. сил
Сформулируем полученное равенство.
Производная по времени от суммарного момента импульсов системы частиц равна сумме моментов внешних сил, действующих на эту систему.
Пусть система замкнута и сумма внешних сил действующих на систему равна нулю (здесь она может быть и не обязательно замкнута, силы могут быть и скомпенсированными, но мы для надежности полагаем ее замкнутой, чтобы различать два эти случая) ,тогда
dL/dt = 0 L = cst.
Для замкнутой системы тел всегда момент импульса есть константа. Здесь сформулирован закон сохранения момента импульса системы тел.
50
