Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный технический университет Украины «Киевский политехнический институт»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Практикум 2

.pdf

Скачиваний:

Добавлен:

17.03.2016

Размер:

5.29 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 258 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Розділ 8. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ ОДНІЄЇ ЗМІННОЇ

Метод уведення функції

f (u(x))u (x)dx f (u(x))du(x)

під знак диференціала

Перетворення диференціалів деяких функцій

dx

1 d(ax b), a,b const;



d(tg x);

cos2 x

 x 1dx

d(x ), 0;



d(ctg x);

sin2 x

d(ln x);

 x



d(arctg x);

1 x2

 cos xdx d(sin x);



d(arcsin x)

 sin xdx d(cos x);

1 x2

Метод інтегрування

формула інтегрування частинами:

частинами. Якщо функції u(x) та

udv uv vdu.

v(x) неперервно диференційовні на

деякому проміжку, то на цьому

проміжку правдива

Типи інтегралів, до яких застосовують інтегрування частинами

(Pn(x) — многочлен степеня n)

sin x



u Pn(x)

P (x) cos x

 Pn(x) ln xdx

u ln x

 Pn(x) arcf xdx

u arcf x

Двічі інтегрувати частинами

sin bx

sin(ln x)



dx,

рівняння щодо шуканого інтеграла.

cos bx

cos(ln x)



Один раз інтегрувати частинами

x2dx,

x2 a2dx

рівняння щодо шуканого інтеграла.

72 Розділ 8. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ ОДНІЄЇ ЗМІННОЇ

8.4. Інтегрування дробово-раціональних виразів

Типи елементарних дробів

Інтегрування елементарних дробів

Adx

Дріб І типу

x a A ln

x a

Дріб ІІ типу

, k 2

Adx

(x a)k

k (x a)k 1

Дріб ІІІ типу

Mx N

D p2 4q 0

x2 px q



Виділяють повний квадрат

у знаменнику

px q



Mx N

Виділяють у чисельнику похідну

від знаменника:

px q

d(x2 px q) (2x p)dx;

Mx N

(2x p)

Дріб ІV типу

Mx N

, D p2 4q 0, k 2

2 px q)k

 Ik

(x2 2 )k

2 2(k

(2n

3)Ik 1

k 1

)



t x

(x2 px q)k

Розкладання раціонального дробу на суму елементарних дробів

Раціональний дріб Pm(x)

Qn(x)

називають правильним, якщо степінь чисельника менше, ніж степінь знаменника.

Будь-який неправильний дріб можна подати як суму многочлена і правильного дробу:

	Pm(x)
			Pm n(x) Rl (x), l n
	Qn(x)		Pm n(x) Rl (x), l n
	Qn(x)

Розділ 8. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ ОДНІЄЇ ЗМІННОЇ

Теорема розкладання. Будь-який правильний раціональний дріб Pm(x)

Qn(x) (n m) можна єдиним чином розкласти на суму елементарних дробів:

Pm(x)											Pm (x)
Qn(x)		(x a )k1				... (x a )kl (x2					p x q			)r1 ... (x2				p x q			)rs
			1							l			1 1		Ak			s		s
						A				A					Ak
							1		2					1
													...				...
				(x a )k1					(x a )k1 1				...		x a1		...
							1		1							Mr x Nr
	M x N				1					M x N		2				Mr x Nr
	1				1				2			2		...			1	1		...
									2 p x q				)r1 1	...						...
(x2 p x q							)r1	(x	2 p x q				)r1 1		x2 p x q				1
			1			1			1			1						1	1

Метод прирівнювання. Праву частину рівності зводять до спільного знаменника, а потім прирівнюють коефіцієнти при однакових степенях x у чисельниках лівої і правої частин.

Метод викреслювання.

Множнику (x a) правильного

A 1

дробу

Pm(x)

, (a)

...

(x a)

a) 1

x a

(x)

(x a)

відповідає розклад

P (x)

(k)

P (x)

(x)

(x a) (x)

(x a)

x a

k 1, 1.

Схема розкладання правильного

Схема інтегрування дробово-

дробу на суму елементарних.

раціонального виразу.

Розкладають знаменник дробу на

Виділяють (у разі потреби) цілу

множники.

частину дробу

Pm(x)

Записують розклад на

Qn(x)

елементарні дроби з невизначеними

Правильний дріб розкладають на

коефіцієнтами.

суму елементарних дробів.

Визначають коефіцієнти методом

Інтегрують суму цілої частини і

прирівнювання або викреслювання.

елементарних дробів.

74 Розділ 8. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ ОДНІЄЇ ЗМІННОЇ

8.5. Інтегрування тригонометричних виразів

Основні способи знаходження I R(sin x, cos x)dx

 Загальний випадок —	t tg	x	dx	2dt
універсальна тригонометрична		2 ,
універсальна тригонометрична		2 ,		1 t2
підстановка		2t			1 t2
	sin x	2t	, cos x		1 t2
	sin x	t2	, cos x		1 t	2
	1	t2			1 t	2
 R( sin x, cos x) R(sin x, cos x)
	I R(cos x)d(cos x)
 R(sin x, cos x) R(sin x, cos x)
	I R(sin x)d(sin x)
 R( sin x, cos x) R(sin x, cos x)
	I R(tg x)d(tg x)

	або I R(ctg x)d(ctg x)
Знаходження sinm x cosn xdx
m 2k 1, k	sin2k 1 xdx sin x(sin x)2k 2dx

(1 cos2 x)k 1d(cos x)

n 2k 1, k

cos2k 1 xdx (1 sin2

x)k 1d(sin x)

m 2k, n 2l, k, l

sin2k x cos2l x

1 cos 2x

1 cos 2x l

m 2

 tg

xdx tg

x tg

cos

m 2

 ctg

xdx ctg

x ctg

1 dx

sin

 sin kx cos lxdx 21 sin(k l)x sin(k l)x dx

cos kx cos lxdx 21 cos(k l)x cos(k l)x dx

sin kx sin lxdx

1 cos(k l)x cos(k l)x dx

Розділ 8. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ ОДНІЄЇ ЗМІННОЇ

8.6. Інтегрування ірраціональних виразів



Виносять старший коефіцієнт і

виділяють повний квадрат під

ax2 bx c

коренем.



Ax B

dx,

Виділяють у чисельнику похідну від

підкореневого виразу:

ax2 bx c

d(ax2 bx c) (2ax b)dx;

Ax B

(2ax b)



(x ) ax2 bx c

 R x, Xr1 s1 , ..., Xrn

sn dx,

ax b tm,

cx d

де X

ax b

m HCK(s1, ..., sn )

cx d

Інтегрування диференціального бінома xm(a bxn )pdx, m, n, p

(теорема Чебишова)

ІІ

ІІІ

m 1

m 1 p

У решті випадків

x tk ,

інтеграл не

k НСК(s1, s2 ),

a bxn

ts,

ax n b ts,

виражається в

елементарних

n r2 , m r1

функціях.

Тригонометричні підстановки



R(x, a

)dx

x a sin t, t

;



R(x, a

)dx

;

x a tg t, t



R(x, x

)dx

, t

cos t

76	Розділ 8. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ ОДНІЄЇ ЗМІННОЇ

Модуль 1. ГРАНИЦЯ ФУНКЦІЇ. НЕПЕРЕРВНІСТЬ

1. Множини. Функції

Навчальні задачі

1.1. Методом математичної індукції довести, що

1 2 2 3 3 4 ... n(n 1) n(n 1)(n 2). 3

Розв’язання. [4.3.4.]

[Крок 1. Перевіряємо правдивість твердження для n 1.]

Для n 1 рівність правдива:

1 2 1(1 1)(1 2). 3

[Крок 2. Припускаючи правдивість твердження для n k, доводимо твердження для n k 1.]

Нехай ця рівність правдива при n k :

1 2 2 3 3 4 ... k(k 1) k(k 1)(k 2). 3

Доведімо, що рівність правдива і при n k 1, тобто

1 2 2 3 3 4 ... k(k 1) (k 1)(k 2) (k 1)(k 2)(k 3).
Справді,	3

1 2 2 3 3 4 ... k(k 1) (k 1)(k 2)
k(k 1)(k 2) (k 1)(k 2)	(k 1)(k 2)(k 3).
3	3

[Крок 3. Висновуємо правдивість твердження для будь-якого n. ]

1.2.Розкласти біном (a b)6.

Розв’язання. [4.15.5, 4.15.9, 4.16.2–4.16.4.]

[Виписуємо формулу для бінома у згорнутому вигляді і розгортаємо його.]

(a b)6 C6ka6 kbk

C60a6b0 C61a5b1 C62a4b2 C63a3b3 C64a2b4 C65a1b5 C66a0b6

[Обчислюємо біноміальні коефіцієнти.]

C 0

C 6

C 5

6 !

6; C 2

C 4

6 !

6 5 15;

1 ! 5 !

2 ! 4 !

5 4

C 3

6 !

20.

3 ! 3

2 3

78	Модуль 1. ГРАНИЦЯ ФУНКЦІЇ. НЕПЕРЕРВНІСТЬ

[Підставляємо знайдені коефіцієнти в розклад.]

(a b)6 a6 6a5b 15a4b2 20a3b3 15a2b4 6ab5 b6.

1.3.Записати усі підмножини множини M {1, 2, 3}.

Розв’язання. [4.4.3.]

Порожня множина є підмножиною будь-якої множини. Одноелементні підмножини множини M : {1}, {2}, {3}. Двоелементні підмножини множини M : {1, 2}, {1, 3}, {2, 3}. Триелементна множина M {1, 2, 3} є своєю підмножиною.

Множина M має 23 8 підмножин:

, {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}, {1, 2, 3}.

1.4. Задано множини
A {x : x 1	1}, B {x : x 1	2}.

Знайдіть і зобразіть множини A, B, A B, A B, A \ B, B \ A.

Розв’язання. [4.4.5–4.4.7.]

[Знаходимо множини A та B, розв’язуючи відповідні нерівності.] x 1 1 1 x 1 1; 0 x 2.

x 1	x 1	2,	x 1,
x 1	2
		2
	x 1	2	x 3.

[Зображуємо знайдені множини на числових осях. Решту множин можна знаходити як аналітично, так і графічно.]

A (0; 2);				x	A
		0	2
B ( ; 3] [1; );					B
	3	1		x
A B ( ; 3] (0; );					A B
	3	0		x
A B [1; 2);					A B
		1		x
A \ B (0; 1);					A \ B
				x
		0
B \ A ( ; 3] [2; ).					B \ A
	3		2	x

Рис. до зад. 1.4.

1.5. Знайти sup A, inf A, max A, min A, якщо A [0; 2).

Розв’язання. [4.1.7.]

Оскільки x [0; 2) x : x x , то ця множина не має найбільшого елемента.

Множина верхніх меж A — це множина [2; ) з найменшим елементом 2, який і є точною верхньою межею множини [0; 2). Отже, sup A 2.

Множина нижніх меж — це множина ( ; 0] з найбільшим елементом 0 A, який і є точною нижньою межею множини A. Отже, min A inf A 0.

		1. Множини. Функції		79
			x,	x 0,
		1	x,	x 0,
1.6.	Знайти f ( 2), f (0), f(1),
1.6.	Знайти f ( 2), f (0), f(1),	якщо f (x)
			x	0 x .
			2 ,	0 x .

Розв’язання.

Маємо функцію, що задана різними формулами на різних проміжках. Оскільки,2 0, 0 0, то значення f ( 2), f (0) знайдімо за формулою f (x) 1 x :

f ( 2) 1; f (0) 1.

Оскільки 1 0, то значення f (1) знаходимо за формулою f (x) 2x : f (1) 2.

1.7.Визначити функцію f (x), яка справджує умову f (x 1) x2 3x 2.

Розв’язання.

Нехай x 1 t, тоді x t 1. Отже,

f (t) f (x 1) x2 3x 2 t2 5t 6 f(x) x2 5x 6.

1.8.Продовжити функцію y x2, x (0; ) на ( ; 0] так, щоб продов-

жена функція на стала: а) парною, б) непарною:

Розв’язання. [5.2.2–5.2.4.]

Нехай продовжуємо функцію на проміжок	( , 0) виразом	y g(x), та
y(0) a.
а) для парності функції потрібно, щоб
x ( ; 0) y(x) g(x) y( x) f ( x) x2,
y(0) a y( 0) a	a .

б) для непарності функції потрібно, щоб

x ( ; 0) y(x) g(x)

y( x) f( x) x2; y(0) a y( 0) a a 0.

Отже,

а) y(x) x2, x ( ; 0), y(0) ; (рис. 1); б) y(x) x2, x ( ; 0] (рис. 2).

y(0)

O x

Рис. 1 до зад. 1.8

Рис. 2 до зад. 1.8

1.9.Знайти обернену функцію до функції y 2x 5 і визначити її область

означення.

Розв’язання. [4.7.6, 5.1.8.]

Для функції f (x) 2x 5, D(f ) E(f ) .

Функція f (x) зростає для всіх x . Отже, вона має обернену функцію на . Розв’яжімо рівняння y 2x 5 щодо x :

80	Модуль 1. ГРАНИЦЯ ФУНКЦІЇ. НЕПЕРЕРВНІСТЬ

y 2x 5 x y 5 . 2

Оберненою до f функцією є функція y x 5 , x . 2

1.10. Знайти композиції f g і g f, вказати їхні області означення, якщо f (x) x2, g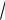(x) x;

Розв’язання. [4.7.7, 5.1.7.]

D(f ) , D(g) [0; ).

E(g) [0; ) D(f );

(f g)(x) f(g(x)) (x)2 x,

D(f g) {x D(g) | g(x) D(f )} [0, ). E(f ) [0; ) D(g);

(g f )(x) x2 x .

D(g f ) {x D(f ) | f (x) D(g)} .

Отже,

(f g)(x) x, x [0; ); (g f )(x) x , x .

Задачі для аудиторної і домашньої роботи

1.11.Замініть крапки виразами «достатньо, але не необхідно», «необхідно, але не достатньо», «необхідно й достатньо» і запишіть висловлювання символічно так, щоб утворились істинні твердження:

1)для того щоб виграти в лотереї, ... мати хоча б один лотерейний квиток;

2)для того щоб сума двох дійсних чисел була числом раціональним, ...

щоб кожен доданок був раціональним числом;

3)для того щоб трикутник був рівнобедреним, ... щоб кути при основі були рівні.

1.12. З’ясуйте зміст висловлювань	і встановіть, істинні вони чи хибні
(x, y ):
1) x y : x y 3;	2) y x : x y 3;
3) x,y : x y 3;	4) x, y : x y 3.

1.13.Методом математичної індукції доведіть, що для будь-якого n :

1)n(2n2 3n 1) ділиться націло на 6;

2)n5 n ділиться націло на 5;

<<< < Предыдущая 1 2 3 4 5 6 78 / 258 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.03.2016102.13 Кб5Практика МУФ.docx
#
09.11.2019157.7 Кб0Практика НМ.doc
#
12.05.201528.08 Кб7практика, мова1.docx
#
12.05.2015165.58 Кб14практика.pdf
#
17.03.2016393.04 Кб15ПРАКТИКА_ФММ1.docx
#
17.03.20165.29 Mб50Практикум 2.pdf
#
12.05.20155.25 Mб9Практикум2013.pdf
#
17.03.20162.86 Mб47Практикум_Ромашко.pdf
#
12.05.201524.81 Кб176Практичні роботи.docx
#
14.11.201954.78 Кб3Практична робота 2.doc
#
11.09.2019205.82 Кб1Практична робота 3.doc