Мультипликативный критерий

Аддитивный критерий основан на использования принципа справедливой компенсации значений нормированных частных критериев. Но в ряде задач проектирования более целесообразным является оперирование не с абсолютными, а с относительными изменениями значений частных критериев.

Принцип справедливой относительной компенсации формулируется следующим образом: справедливым следует считать такой компромисс, когда суммарный уровень относительного снижения значений одного или нескольких критерий не превышает суммарного уровня относительного увеличения других критериев.

В математической формулировке условие оптимальности на основе принципа справедливой относительной компенсации имеет вид

(3)

где ΔF_i(X) – приращение величины i – го критерия, F_i(X) – первоначальная величина i – го критерия.

Полагая , можно представить (3) как дифференциал натурального логарифма

(4)

Из выражения (4) следует, что принцип относительной компенсации приводит к мультипликативному обобщённому критерию оптимальности

(5)

Мультипликативный критерий образуется путём простого перемножения частных критериев в том случае, когда они имеют одинаковую важность. В случае неравноценности частных критериев вводятся весовые коэффициенты _i и мультипликативный критерий примет вид

(6)

Мультипликативный критерий иногда представляется в виде отношения произведений частных критериев (выходных параметров)

m₁+m₂=m; (7)

где в числителе перемножаются все выходные параметры, требующие максимизации и имеющие ограничения а в знаменателе – все выходные параметры, требующие минимизации и имеющие ограничения, гдеTT_i – значение технического требования, предъявленного к i– му критерию. Целевая функция (7) в дальнейшем подвергается максимизации.

Достоинством мультипликативного критерия является то, что при его использовании не требуется нормирование частных критериев. Недостатки критерия: критерий компенсирует недостаточную величину одного частного критерия избыточной величиной другого и имеет тенденцию сглаживать уровни частных критериев за счёт неравнозначных первоначальных значений частных критериев.

Примеры 1. Производственная функция, отражающая овеществлённый технический прогресс (модель Р. Солоу):

где Y_t – выпуск продукции; L – численность рабочих; K – объём основных производственных фондов. Здесь величины  и 1- следует рассматривать как весовые коэффициенты.

Пример 2. Обнаружение сигналов в "белом" шуме. На вход RC – фильтра с импульсной характеристикой поступает аддитивная смесь: прямоугольный импульсs(t) плюс "белый" шум n(t). Требуется найти такое значение , чтобы отношение сигнал/шум было максимальным, т.е. мы желаем, чтобы значение сигнала было максимальным, а уровень шума – минимальным ( – полоса пропускания RC – фильтра).

Рис.3. Сигнал s(t) Рис 4.Шум n(t)

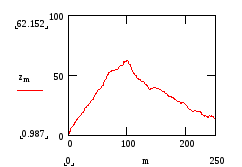
Рис. 5.Сигнал плюс шум Рис.6. Отфильтрованный сигнал

Рис. 7.Система обнаружения сигнала

F₁()=A(1-e^-T)  max (уровень сигнала на выходе фильтра),

F₂()= min (уровень шума на выходе фильтра).

где A,N,T - константы; F₁ и F₂ - имеют одинаковую размерность. Найти оптимальную полосу пропускания , если справедлив принцип относительной компенсации частных критериев. Согласно формуле (7) мультипликативный критерий будем иметь вид:

Пример. Применим мультипликативный критерий оптимальности для определения оптимальных параметров для автомата. Мы получили следующую задачу оптимизации:

найти максимум функции

при ограничении 1.6L+ 0.05N+2≤6.

Для определения максимального значения f(L,N) с учётом ограничения равенства мы будем использовать метод неопределённых множителей Лагранжа. Получим следующую задачу безусловной оптимизации:

найти максимум функции

Находим частные производные по L, N,  и приравниваем их к нулю. Получим систему уравнений:

Решая эту систему, получим следующие значения: N_opt=53, L_opt=0.83 м, V_opt=137 м/cек.

Использование мультипликативного критерия в задаче оптимизации привело другим значениям параметров автомата по сравнению с решением задачи с аддитивным критерием оптимальности. Это объясняется тем, что диапазоны взаимной компенсации абсолютных и относительных изменений частных критериев неодинаковы. Поэтому в каждом конкретном случае технического проектирования следует тщательно анализировать и обосновывать целесообразность учёта либо абсолютных, либо относительных изменений значений частных критериев и в зависимости от степени важности этих отклонений выбирать либо аддитивный, либо мультипликативный критерий оптимальности.

Заключение. Преимущества и недостатки формальных обобщённых критериев.

Преимущества – возможность учёта в качестве f_i(X) любых выходных параметров системы, а также надёжность и стоимость.

Основные недостатки – возможность компенсации ухудшения целевой функции из-за ухудшения одного параметра за счёт улучшения какого-либо другого выходного параметра.