13. Қос интегралдаудың негізгі қасиеттері. Қос интегралдауда және үш еселі интегралдауда айнымалыны ауыстыру.

Екі еселі интеграл. Негізгі қасиеттері

z=f(x,y) D облысында анықталған D:D_i i=1̅,n̅ D_i M(x_i,y_i) f(x_i,y_i) ΔS_i–D_iоблысының ауданы, ∑ⁿ_i=1 f(x_i,y_i) S_i g-облысы бойынша интегралдық қосындысы. lim_n→∞∑ⁿ_i=1 f(x_i,y_i) S_i =∫_D∫f(x,y)dS . Егер f(x,y) үшін интегралдық қосындының n→∞ (maxdi→0) шегі D облысын n бөлікке бөлу әдісіне тәуелсіз ж/е осы облыстан M(x_i,y_i)нүкелерін таңдап алу әдісіне тәуелсіз бар болса онда осы шекті f(x,y) ф/ң D облысы бойынша екі еселі интегралы д.а. мұндағы f(x,y) интегралдық ф/я,dS- бөліктің ауданы. z=(x, y) D олысында шенелген болуы қажеттң ғана .TH:z=(x, y) D олысында үзіліссіз болса онда функция облысы интегралданады, яғни екі еселі интегралы бар. Дарбу ережесі: lim_n→∞(S-s)=0 Қасиеттері:

1.∫∫_D kfdS=k∫∫_DfdS 2.∫∫_D(f₁±f₂)dS=∫∫_D f₁dS+∫∫_D f₂dS

3. D=D₁∩D₂→∫∫_Df(x,y)dS=∫∫_D1f(x,y)dS+∫∫_D2f(x,y)dS

4.f(x,y)>0→∫∫_Df(x,y)>0 f₁≥f₂→∫∫_Df₁≥∫∫_Df₂

5.m≤f(x,y)≤M (облысында үз/сіз болса ең үлкен ең кіші мәні табылады)mS≤∫∫_Df(x,y)dS≤MSЕкі еселі интегралды бағалау

6. ∫∫_Df(x,y)dS=f(x₀,y₀)S f(x₀,y₀)=1/2∫∫_Df(x,y)dS

Үш еселі интегралда айнымалыны ауыстыру

 Егер функциясы V тұйық облысында үзіліссіз болса, ал

(1)

функцияларының UVW кеңістігіндегі Т тұйық облысында үзіліссіз дербес туындылары бар болып және осы облысты XYZ кеңістігіндегі V облысына бірмәнді бейнелесе, онда келесі теңдік орындалады:

(2)

мұндағы - якобиан бейнелеуі

14 Бірінші және екінші текті қисық сызықты интегралдар.

Бірінші түрдегі қисық сызықтыинтеграл - бір айнымалы Риман интегралының жалпылауы. Бір айнымалы Рмиан интегралының S-тіліндегі анықтамасы: функциясысегменінде анықталсын. Егер қасыбірнақты сан мен әроң саны үшін_{n- 1}…, N) болған сайын

<

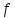болатындай оң саны табылса, ондафункциясысегменінде интегралданады,санын оның интегралы деп атайды да, ол үшін

(1) Белгілеуі қолданылады.

Қисық ұғымын қолданып, бұл анықтаманы былай жалпылауға болады. үзіліссіз дифференциалданатын жай қисығы беріліп,:Жиынынданақты мәнді функциясы анықталсын. Әрүшінқисығыныңнүтелер арасындағы бөлігінің ұзындығы

(2) болады.

сегменің _nбөлшектеуі берілсін. Онда үшін айырымы қисығының _{- 1}және . 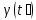нүктелерін жалғайтын бөлігінің ұзындығы болады. Осы дайындықтан кейін, мақсатымыз болатын анықтамаға тікелей көше аламыз. Егер қасыбірнақты сан мен әроң саны үшін_{n- 1}…, N) болған сайын

<

болатындай оң саны табылса, ондафункциясықисығында интегралданады, алсанын оның интегралы дейді де

(3)белгілеуі қолданылады.

(3) интегралы бірінші түрдегі қисықсызықты интеграл деп атайды. Егерде сегменінде анықталғанфункциясын жазықтықта жатқанқисықтың бейнесі болатынсегменінде анықталғанфункция ретінде қарастырсақ, онда (3) анықтамасы (1) анықтамасына айналады. Сөйтіп бірінші түрдегі қисық сызықты интеграл анықтамасы бір айнымалы функцияның интеграл анықтамасының жалпылауы болады.

Екінші түрдегі қисықсызықты интеграл. Ω облысы беріліп, Р (x,y) және Q(x,y) функциялары Ω облысында анықталған және үзіліссіз болсын.

γ (t) = (x(t), y(t)) (a ≤ t ≤ b) қисығы үзіліссіз дифференциалданып, әр t[ a, b ] үшін γ (t) CΩ кірістіруі орындалсын.

w(x,y)=P(x,y)dx+Q(x,y)dy дифферианциалдық формасының γ қисығы бойынша екінші түрдегі қисықсызықты интегралы деп

(1)

саны аталады да, ол не қысқаша(2*)

түрлерінде белгіленеді. Енді екінші түрдегі интегралдың кейбір қасиеттерін атап өтейік.

. Қойылған шарттар (1), демек, (2)-(2*) интегралының бар болуын қамтамасыз етеді.Расында да,қойылған шарт бойынша γ қисығын анықтайтын x(t) және y(t) функциялары [a,b] cегментінде үзіліссіз дифференциалданады, демек, x’(t) және y’(t) функциялары сол сегментте үзіліссіз, бұған қоса Р(x(t),y(t)) және Q(x(t),y(t)) функциялары үзіліссіз функциялардан құрылған күрделі функциялар ретінде [a,b] сегментінде үзіліссіз. Сондықтан (1) интегралы үзіліссіз функциядан алынған интеграл ретінде бар болады.

2. Егерде қисығы γ қисығынан параметрді алмастыру арқылы алынса, онда (2*) интегралымен бірге(3) Интегралы да бар болады.γ мен бірыңғайлы бағытталған жағдайда, яғни t’(u) > 0 болғанда=(4)

Ал қарама-қарсы бағытталған жағдайда, t’(u)<0 болғанда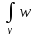=(5) тендіктері орындалады. Расында да, x(t (u)) =(u), y(t(u)) =(u)(6) болсын. Ондақисығы(u) = (дәл озі болады. 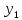Күрделі функцияны дифференциалдау ережесі бойынша’(u) = x’ (t(u)) * t’ (u),’(u) = y’ (t(u)) * t’ (u)(7) Демек,(u) және(u) функциялары [] сегментінде үзіліссіз дифференциалданып, 1б/ша (3) интегралы бар болып,(u)= P((u),(u))’ + Q ((u),(u))(u) (8)=(u)du(9)болады.Сонымен қатар (1) интегралында t = t(u) алмастыруын жасағанда,интеграл астындағы функция

f(u)=P(x(t(u)), y(t(u))) x’(t(u))t’(u)+Q(x(t(u)),y(t(u)))y’(t(u))t’(u) (10)

функциясына алмастырылады.(10)(7)(6)(8) бойыншаf(u)=(u). (11)

γ менбірыңғай бағытталғандаt()=a,t()=b болып, (4)теңдігіне:

= ,

Ал γ мен қарама-қарсы бағытталса t()=b, t(болып,(5)-ке келеміз:

.

Сөйтіп, екінші түрдегі қисықсызықты интеграл, бірінші түрдегідей емес, қисықтың бағытталуына тәуелді екендігі анықталады.

3(қисықсызықты интегралдың сызықтық қасиеті):

= +

4 (қисықсызықты интегралдың аддитивтік қасиеті): егерде a < c < b үшін(t) =γ (t) (a ≤ t ≤ c ) және (t) =γ (t) (c ≤ t ≤ b ) болса, онда

.