10. Сандық қатарлар. Абсолют және шартты жинақты қатарлар. Қатар жинақтылығының жеткілікті шарттары.

Айталық сан тізбегі берілсін. Егер тізбектін мүшелерін «+» белгісімен тіркестіріп жазсақ, онда(1,1)түріндегі сан қатары деп аталатын өрнекті аламыз. Оны қысқаша былай белгілейді:сандарын қатардың мүшелері деп, ал кез келген нөмірлімүшесін қатардың жалпы мүшесі немесе–мүшесі деп атайды. Қатар мүшесінің белгілі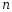нөмері бойынша, бұл мүшені жазу ережесі белгілі болса, онда қатарды берілген дейді. Қатардың алғашқымүшелерінің қосындысын қатардың-дербес қосындысы дейді. Оны былай белгілейді:

Ал, қатардың мүшелерінің саны шексіз болғандықтан, оның дербес қосындылары деребес қосындылардың шексіз тізбегін құрайды:

Қатар қосылғыштардың шексіз жиындарынан құрылатын болғандықтан, оларды тізбектей біртіндеп қосу арқылы қатар қосындысын анықтау мүмкін емес. Сондықтан, қатар қосындысының анықтамасын келтірейік. Егер 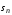дербес қосындысындағы қосылғыштар санын арттырсақ, онда мынандай үш жағдайдың біріне тірелеміз:

1. Дербес қосынды -нің қосылғыштары санын шектеусіз арттырғанда, ол белгілі бір шекке ұмтылады, яғниболады. Бұл жағдайда, қатарды жиынақты деп, алсанын оның қосындысы деп атайды. Сонымен

2. Дербес қосындыдағы қосылғыштар саны шектеусіз артқанда

немесе болады. Бұл жағдайда,

қатарды жинақсыз /шашыранды/ дейді. Шашыранды қатардың қосындысы болмайды.

_3. Дербес қосындыдағы қосылғыштар саны шектеусіз артқанда, дербес қосынды ешқандай шекке ұмтылмайды. Бұл жағдайдан да қатарды жинақсыз болады дейді және қатардың қосындысы болмайды. Сонымен, тек жинақты қатардың ғана қосындысы болады екен:

_{Абсолютті жинақталған қатардың жинақталуы.}

сандық қатары берілсін. Егер осы қатардың әр мүшесін оның абсолютті шамасына алмастырғанда пайда болатын теріс емес

қатары абсолютті жинақталады дейді.

Теорема. Абсолютті жинақталатын қатар жинақталады.

Дәлелденуі Теорема шарты бойынша қатары жинақталады,демек, Коши критерийі бойынша әрсаны үшінболған сайынболатындайсаны табылады.Дәл осындай кез келген p мен q, демек, тағы да Коши критерийі бойынша, қатары жинақталады.Теорема дәлелденді.

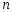Жинақты қатарлардың қасиеттері.1-теорема. Егер (1,1)қатары жинақты және қосындыболса, онда(1,3)(с-берілген сан) қатары да жинақты және оның қосындысыболады.Дәлелдеу. Айталық (1,1) қатардың -дербес қосындысы, ал (1,3) қатардың-дербес қосындысындейік. Сондаболадлы. БұданСонымен, (1,3) қатар жинақты және оның қосындысыболады екен.

2-теорема. Егер (1,1)және(1,4) қатарлары жинақты және олардың қосындылары сәйкесжәнеболса, онда(1,5)қатары да жинақты және оның қосындысы+болады.

Дәлелдеуі: (1,1),(1,4) және (1,5) қатарларының дербес қосындыларын сәйкес жәнедеп белгілейік. Сонда

Енді шекке көшсек

болады. Сонымен, (1,5) қатары жинақты екен. (1,5) қатарын (1,1) мен (1,4) қатарларының қосындысы дейді.

Ескерту. Осы сияқты (1,1) және (1,4) қатарлары жинақты болғанда,

(1,6) қатары да жинақты және оның қосындысы --ке тең болатынын дәлелдеуге болады. (1,6) қатарды (1,1) мен (1,4) қатарларының айырымы дейді. Сонымен жинақты қатарды бір санға көбейтуге, шекті қосындылар тәрізді қатарларды мүшелеп қосуға және азайтуға болады екен.(1,6)қатарын (1,1) қатарының-қалдық мүшесі деп атайды. Ол (1,1) қатардан, оның алғашқымүшелрін шығарып тастаудан алынады.

3-теорема. Егер қатар жинақты болса, онда оның кез келген қалдығы да жинақты болады. Егер қатардың қандай бір қалдығы жинақты болса, ол қатар да жинақты болады.

Дәлелдеу: Айталық қатары жинақты және қосындысыяғниболсын. Бұл қатардың шығарылып тасталған мүшелерінің қосындысын, ал алғашқымүшелерінің қосындысындейік. Сонда(1,7). Мұндағысаны-ге тәуелді емес белгілі бір сан. (1,7) теңдігінен

яғни (1,6) қатардың дербес қосындысының тізбегі -ның шегі бар болады. Сондықтан (1,6) қатары жинақты. Енді айталық (1,6) қатары жтнақты және оның қосындысыболсын дейік, яғнтдейік. Сонда (1,7) ден

Бұл (1,1) қатардың жинақты болатынын дәлелдейді.

Жинақты болудың қажетті шарты. Қатараларды қарстыруда мынандай екі мәселе туады:

1) қатардың жинақты, не жинақсыз болатынын анықтау, және 2)қатар жинақты болған жағдайда, оның қосындысын табу.

4-теорема. Егер қатары жинақты болса, онда оныңжалпы мүшесінөмірі шектеусіз өскенде нолге ұмтылады, яғни

Дәлелдеу.Айталық қатары жинақты және оның қосындысыболсын. Оның

және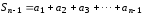дербес қосындыларын қарастырайық. Бұлардан

Сондықтан,

Өйткені және. Мұнда-да. Сонымен,екен.

Салдар. (Қатардың жинақсыз болуының жеткілікті шарты.)

Егер қатардың жалпы мүшесі нөмірі шектеусіз артқанда нөлге ұмтылмайтын болса, онда қатар жинақсыз болады.

Шынында, егер қатарды жинақты десек, онда алдыңғы теоремаға сәйкес қатардың жалпы мүшесі нолге ұмтылған болар еді. Бірақ, бұл шартқа қайшы. Сондықтан, қатар жинақсыз.