5. Дифференциалданатын функциялардың негізгі қасиеттері. Бір айнымалы функция үшін Тейлор формуласы.

Y=f(x) ∆y=f(x₀+∆x)-f(x₀)

Lim{∆x→0}∆y/∆x=fꞌ(x₀) lim{∆x→0}α(∆x)=0

∆y/∆x=fꞌ(x₀)+α(∆x)

∆y=A∆x+α(∆x)*∆x

Анықтама:Функцияның өсімшесінің (∆y) ∆xқарағандағысызықты,еңбастыбөлігінсолфункцияның дифференциалы депатайды.

Dy=A*∆x=fꞌ(x)*∆x

yꞌ,dy/dx ∆x=dx

y=x

dy=dx=1*∆x

∆y͌≈dy

F(x₀+x)-f(x₀)≈fꞌ(x₀)*∆x

F(x₀+∆x) ≈f(x₀)+fꞌ(x₀)*x

Мысалы:arctg 1,05=?

y=arctgx

x₀=1 yꞌ=1/1+x²

∆ x=0,05 fꞌ(x₀)=0,5

f(x₀)=π/4

arctg1,05≈3,14/4+0,5*0,05=0,785+0,025=0,810

6. Функцияның интегралдануының қажетті және жеткілікті шарттары. Анықталған интегралдың орта мәні туралы теоремалар.

Анықталған интегралдың анықтамасы. сегментінде анықталғанфункциясы берілсін. Осы сегментті қалауымызша алынғаннүктелеріменбөлікке бөліп, әрбөлік сегменттен кез келген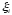нүктесін алып, Риман қосындысы немесе интегралдық қосынды деп аталатын мынадай қосынды жасайық:.

Бұл қосындының мәні, жалпы алғанда, сегментін бөлу тәсілінен де,нүктелеріне де тәуелді. Бөлік сегменттердің ұзындықтарының ең үлкенін, яғнидеп белгілейік.

Анықтама. Егер интегралдық қосынды 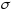-ныңнөлге ұмтылғанда (барлық бөлік сегменттердің ұзындықтарынөлге ұмтылғанда)сегментін бөлу тәсілінен тәуелсіз және әр бөлік сегменттеннүктесін таңдап алудан тәуелсіз шекті (тиянақты) шегі бар болса, осы шектіфункциясының-дан-ға дейінгі немесесегментіндегі анықталған интегралы деп,атайды да оныдеп белгілейді..

Мұндағы - интеграл астындағы функция,- интеграл астындағы өрнек,саны –интегралдың төменгі,саны – интегралдың жоғарғы шегі, алайнымалысы – интегралдау айнымалысы деп аталады.

Берілген анықтамадан жоғарғы, төменгі шектер тұрақты сандар болса, анықталған интеграл тұрақты санға тең болатынын байқаймыз, себебі ол айнымалы қосындының шегі.

Риман бойынша кесіндісінде интегралдагатын барлық функциялар жиынынарқылы белгілейді.

1-теорема. (қажетті шарт ) кесіндісінде анықталғанфункциясының осы кесіндіде Риман бойынша интегралдануы үшін оның осы кесіндіде шектеулі болуы қажет.

2 –теорема. (жеткілікті шарт) кесіндісінде шектелгенфункциясының осы интервалда интегралдануы үшін кезкелгенсаны табылып, параметріболатынкесіндісінің кезкелгенбөліктеуі үшінтеңсіздігінің орындалуы жеткілікті.

Анықталған интегралдың орта мәні туралы теорема.

Егер функциясысегментінде интегралданса жәнеүшінтеңсіздіктері орындалса, оның интегралытеңдігін қанағаттандырады,мұндағытеңсіздігін қанағаттандыратын тұрақты сан.

7. Бірінші және екінші текті меншіксіз интегралдар. Меншіксіз интегралдардың жинақтылығының жеткілікті шарттары.

Риман интегралы сегментте (тұйық шенелген аралықта) анықталған және шенелген функция үшін анықталған еді. Осыған орай, мұнда Риман интегралы, біріншіден, шенелмеген аралық, екіншіден, шенелмеген функция жағдайларына жалпыланады. Бұл жалпылаулар Риман интегралы анықтамасына негізделіп, шекке көшу арқылы жүргізіледі де, пайда болған интеграл меншіксізинтеграл деп аталады (әрине, онда бастапқы Риман интегралы меншікті интеграл деп аталуы тиісті де, солай аталады да).

Сөйтіп, Риман интегралының өзі де шек екендігін ескере отырып, меншіксіз интеграл қайталанған шектің тағы бір түрін құрайтының көреміз.

Егерде нақты мәнді шегі бар болса, ондафункциясыаралығында Риман бойынша интегралданады депсанының өзін сол функцияныңменшіксізинтеграл деп атап, оны

(1) символымен белгілейді. Бұл жағдайда «(1) интегралы жинақталады» деп те атайды.

Сөйтіп, (1) интегралының жинақталуынефункциясыныңаралығында интегралдануы=(2) шарты орындалуымен парапар.

Меншіксізинтегралдың қасиеттері:

аралығында анықталған функциясы әрсегментінде интегралданады деп алдын-ала ұйғарамыз.

. Егерде,аралығында анықталғанфункциялары үшінменшіксіз интегралды бар болса, онда әржәненақты сандары үшінфункциясы сол аралықта интегралданып,

(12)

теңдігі орындалады.

2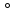.меншіксіз интегралы жинақталуы үшін оның әр қалдық интегралы, яғни,болғандағыинтегралыжинақталуы қажетті де жеткілікті және олар жинақталған жағдайда

(13)

теңдігі орындалады.(13)теңдігін меншіксіз интегралдың аддитивтік қасиеті деп те атайды.

Ескерту.Бірінші және екінші текті меншіксіз интегралдардар жоқ!!!!!

8. Көп айнымалыдан тәуелді функция. Көп айнымалыдан тәуелді функцияның шегі. Көп айнымалыдан тәуелді функция үшін Тейлор формуласы.

Көп айнымалылы функциялар үшін Тейлор формуласы.

f(x) Eашық жиынында анықталып, f(x)кірістіруін қанағаттандырсын, яғни Е жиынының әрбір нүктесінде f(x) функциясының реті s–тен аспайтын барлық мүмкін дербес туындылары бар және үзіліссіз болсын. a=(және x=()E нүктелерін жалғайтын кесінді Е жиынында толық жатсын, яғни-(i=1,2,…,n), h=() үшін t[0,1] болғанда a+th==()болсын. Онда [0,1] сегментінде

f(a+th)=f((1)

күрделі функциясы анықталған болады. fболғандықтанкірістіруі орындалады, яғнибір айнымалы функциясы [0,1] сегментінде s рет үзіліссіз дифференциалданады, сол себептен (1) функциясы үшінболғандағы((2)-теңдігі орындалады. Сонымен бірге,(1) бойынша,(2) теңдігіндедеп алып, бұл жағдайда1 болатынын ескере отырып,

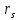f(-f()=f(=+(3)

теңдігіне келеміз. Егер (3) теңдігінде көмекші функциясынан бастапқы f функциясына толық көшсек, онда солай түрлендірілген (3) теңдігі көп айнымалылыТейлор формуласы деп аталады.

9 Көп айнымалыдан тәуелді функцияның локалды экстремумы. Локалды экстремумның қажетті және жеткілікті шарттары. Шартты экстремум.

сандық функциясы ашық жиынында анықталсын. Егер , біріншіден,нүктесіжиынының ішкі нүктесі болса, екіншіден,кірістіруі орындалатындай қайсыбіроң саны мен әрбірүшінтеңсіздігі орындалса, онданүктесінфункциясы локальді максимум мәнін қабылдайтын нүкте, не қысқаша- локальді максимум нүктесі деп атайды. Егертеңсіздігі орындалса, онданүктесінфункциясы локальді минимум мәнін қабылдайтын нүкте, не қысқаша- локальді минимум нүктесі деп атайды.

Экстремум бар болуының қажетті шарты. Егер нүктесіфункциясы үшін локальді экстремум нүктесі болып,функциясыныңнүктесінде барлық дербес туындылары бар болса, онда сол дербес туындылары міндетті түрде нольге тең болады, яғни(1)

Экстремумның жеткілікті шарттары (екі айнымалы жағдайы).

1 – теорема. Екі айнымалы сандық функциясы 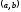нүктесінің қайсыбір- маңайында анықталып, сол маңайда

дербес туындылары бар және үзіліссіз болып, сол нүктенің өзінде локальді экстремумның қажетті шарты орындалсын:

(2)

Мынадай белгілеулер енгізейік:

(3)

. Онда 1) егер болса, онда локальді экстремум нүктесі болып, болғанда локальді қатаң минимум,болғанда локальді қатаң максимум нүктесі болады;

егер болса, онда нүктесі локальді экстремум нүктесі емес;

егер болса, онда нүктесі туралы нақты ештеңе айтуға болмайды; ол локальді экстремум нүктесі болуы да, болмауы да мүмкін.

Шартты экстремум. сандық функциясы жиынында анықталып,жиыны берілсін. Егер: 1°. нүктесі Е жиынының ішкі нүктесі болса; 2°. а нүктесі F жиынында жатып, сол жиынның шектік нүктесі болса, яғни а нүктесінің әрбір маңайында а-дан өзге болатын F жиынының нүктесі табылса; 3°. а нүктесінің белгілі бір маңайы мен F жиынында жатқан әрбір нүктесі үшінтеңсіздігі орындалса, яғни

(V_δ (a)

болса, онда а нүктесінf функциясыныңF бойынша шартты максимум (шартты минимум) нүктесі деп атайды. Әдеттегідей, шартты максимум мен шартты минимум шартты экстремум деп аталады.

Шартты экстремумның кажетті шарты.

Диференцианалданатын f функциялары арқылы

ψ(x₁,x₂,...,x_n) = f(x₁,x₂,...,x_n,φ₁(x₁,x₂,...,x_n),..., φ_m (x₁,x₂,...,x_n))

бойынша анықталған ψ(x₁,x₂,...,x_n) күрделі функциясы да сол маңайда дифференциалданады. Сондықтан локальді экстремумның қажетті шарттын қолданып келесі теңдеуге келеміз:

(a₁,a₂,...,a_n)=0 ,... ,(a₁,a₂,...,a_m)=0 бұған байланыс теңдеудері беретін

F₁ (a₁,a₂,...,a_n+m)=0, ... , F_m (a₁,a₂,...,a_n+m)=0 теңдеулерін қосып, саны n+m болатын a₁,a₂,...,a_n+m белгісіз айнымалыларын табу үшін n+m теңдеу алдық. Осы теңдеулер шартты экстремумның қажеттін шартын құрайды.

Шартты экстремумның жеткілікті шарты.

x₁=a₁,...,x_n+m=a_n+m, λ₁= λ⁽⁰⁾₁, ... ,λ_m=λ⁽⁰⁾_m сандары

=0, ... ,=0;=0, ... ,=0 (1)

жүйесінің шешімін құрасын. Онда Ф(x)=f(x)+λ⁰₁F₁(x)+...+λ⁰_mF_m(x) Лагранж функциясы үшін

(2)

жүйесі n айнымалылы Q квадраттық формасын анықтайды.