24. Дать определение гиперболы. Записать каноническое уравнение гиперболы, основные хар-ки. Изобразить на рисунке.

Ответ: Гиперболой назыв. множество точек плоскости, абсолютная величина разности от каждой из которых до 2 данных точек, называемых фокусами, есть величина постоянная.

Для вывода уравнения гиперболы выберем систему координат таким образом, чтобы ось ОХ проходила через фокусы, а ось ОУ проходила через середину отрезка, соединяющего фокусы.

Пусть М(х,у) – произвольная точка гиперболы.

Обозначим расстояние между фокусами через 2с: │F₁F₂│=2c, а абсолютную величину разности расстояний отточек гиперболы до фокусов – через 2а. Тогда можно записать:

│F₁M│-│F₂M│=2a,

где F₁M и F₂M – фокальные радиусы точки М. Данное равенство, дважды возведя в квадрат и обозначив с²-а²=в², можно привести к виду:

х² _ y²

a² в² = 1. – простейшее (каноническое) ур-ние гиперболы.

Т.к. переменные х и у входят в уравнение гиперьолы во 2ой степени, то гипербола симметрична и отностительно ОХ , и относительно ОУ.

Выразим из уравнения гиперболы у:

у² х² _

в² = а² 1,

у² х² –а²

в² = а² ,

в² + в² ______

у²= а² (х² – а²), у = - а² √ х² + а² ,│х│≥а ,т.е. между прямыми х=а и х=-а точек гиперболы нет.

Аналогично выразим из уравнения гиперболы х:

+ а ______

х = - в √у² – в² , => у (-∞; ∞).

При возрастании х от а до +∞ у изменяется от 0 до +∞.

Асимптоты гиперболы:

+ в х;

у = - а

Эстентриситетом гиперболы назыв. отношение расстояний между фокусами к длине действит. оси:

2а а √а²+в²

ε = 2с = с = а (т.к. в²=с²-а²);

25. Дать определение параболы. Записать каноническое уравнение параболы, основные характеристики. Изобразить на рисунке.

Ответ: 43. Парабола и ее уравнение.

Параболой называется множество точек плоскости, одинаково удаленных от данной точки, называемой фокусом и от прямой, называемой директрисой.

Для вывода уравнения параболы выберем систему коорднат таким образом, чтобы ось ОХ проходила через фокус перпендикулярно директрисе, а ось ОУ – через середину отрезка, соединяющего фокус и директрису.

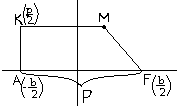
Пусть М – произольная точка параболы. Обозначим расстояние между фокусом и директрисой через Р Из определения параболы следует, что │FM│=│KM│. Запишем это равенство в координатной форме:

√(х – р/2)² + (у-0)² = √х- (- р/2)² + (у-у)² или √(х – р/2)² + у² = √х+ (р/2)^2.

Возведем обе части в квадрат:

(х – р/2)²+у² = (х+р/2)²;

х²-рх+ (р²/4) + у2 = х² + рх + (р²)/4;

у²=2рх – канонической уравнение параболы.

Т.к. переменная у во второй степени, парабола симметрична отности. оси ОХ.

Т.к. точка 0 удовлетворяет уравнению, то значит, парабола проходит через начало координат.

Парабола располагается правее оси ОУ, т.к. 2рх должно быть ≥ 0.

При возрастании х от 0 до +∞ у изменяется от 0 до +∞.

Если ветви параболы направлены влево от оси ОУ, то уравнение имеет вид: у²= - 2рх;

Если ветви параболы наход. направлены вверх от оси ОХ, а фокус наход. на оси ОУ уравн. имеет вид: х²=2ру;

Если ветви параболы направлены вниз, а фокус расположен ниже ОХ, то уравн.имеет вид: х²= - 2ру.