30. Определить уравнение прямой, как линии пересечения двух плоскостей. Вывести уравнение прямой, проходящей через две заданные точки.

Прямая, как линия пересечения двух плоскостей

Направляющий вектор этой прямой:

Прямая, проходящая через две заданные точки

Пусть даны 2 точки:

31. Дать определение предела функции в точке и на бесконечности. Определить односторонние пределы. Сформулировать свойства пределов функций. Записать замечательные пределы.

Предел функции в точке и на бесконечности

Число называется пределом функции в точке , если для любого сколь угодно малого числа найдётся такое число , зависящее от , что для всех , таких, что выполняется неравенство

Число называется пределом функции при , если для любого числа найдётся такое число , что для всех выполняется неравенство .

Аналогично определяется предел функции при .

Односторонние пределы

Свойства пределов функций:

Замечательные пределы

Первый замечательный предел.

Второй замечательный предел.

32. Показать различные способы вычисления пределов функции в точке и на бесконечности.

Чтобы раскрыть неопределённость , заданную отношением двух многочленов, надо числитель и знаменатель разложить на множители и сократить множители, равные 0 при предельном значении переменной.

Пример:

Чтобы раскрыть неопределённость , в которой числитель или знаменатель содержит иррациональность, следует избавиться от иррациональности следующим образом: домножить выражение на сопряжённое.

Пример:

Чтобы раскрыть неопределённость , заданную отношением двух многочленов, надо числитель и знаменатель разделить на самую высокую степень.

Пример:

Если степень числителя равна степени знаменателя, то предел равен отношению коэффициентов при старшей степени.

Если степень числителя меньше степени знаменателя, то предел равен 0.

Если степень числителя больше степени знаменателя, то предел равен

33. Дать определение функции непрерывной в точке и на промежутке. Перечислить свойства функций непрерывных в точке. Дать определение точек разрыва функции. Классифицировать точки разрыва.

Непрерывность функции в точке

1. а) Функция называется непрерывной в точке 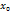, если она определяется в некоторой

Если обозначить – приращение аргумента и – приращение функции, то получим определение б)

б) Функция называется непрерывной в точке , если она определена в

некоторой окрестности этой точки и бесконечно малому приращению аргумента

соответствует б.м. приращения функции.

2. Одностороння непрерывность

Функция называется непрерывной слева в точке , если она определена на

Функция называется непрерывной справа в точке , если она определена на

Функция непрерывна в точке тогда и только тогда, когда она непрерывна слева и справа в этой точке.

Непрерывность функции на промежутке

Функция называется непрерывной, если она непрерывна в каждой точке этого промежутка. В частности называется непрерывной на отрезке , если она непрерывна в каждой точке интервала , непрерывна справа в точке и слева в точке

Свойства функций, непрерывных в точке

1.Пусть непрерывны в точке , тогда непрерывны

2.Все простейшие элементы функции:

непрерывны в каждой точке своей ОДЗ.

Точки разрыва функции и их классификация

Точки, в которых нарушена непрерывность функции, называются точками разрыва этой функции.

Точка разрыва называется точкой разрыва 1-го рода функции , если в этой точке существуют конечные пределы функции слева и справа

При этом:

1)Если , то точка называется точкой устранимого разрыва.

1) Если , то точка называется точкой конечного разрыва. – скачок функции.

Точка разрыва называется точкой разрыва 2-го рода функции , если по крайней мере один из односторонних пределов слева или справа не существует или равен