44. Сформулировать правила Лопиталя, раскрытия неопределённостей Привести пример

Если заданы 2 фун-ции эти ф-ции диффирин. За исключением точки Mo(x o, yo) и существует неопределенность , при х→∞, тогда = = =…=

Пример

45. Сформулировать правила Лопиталя, раскрытия неопределённостей вида Привести пример.

1. 

2. 

3. 

46. Записать формулу Тейлора. Формула Маклорена. Вывести формулу Маклорена для функций: у = е^х, у = sinx.

Это выражение называется формулой Маклорена для многочлена  степени .

Это выражение называется формулой Тейлора для многочлена  в окрестности точки  , где  - любое число.

Разложение

Так как (e^x)' = e^x, то производная любого порядка функции e^x равна e^x. При x = 0 функцияe^x и ее производные любого порядка равны одному. Таким образом, формула Маклорена для функции e^x имеет вид

Отметим, что для любого вещественного числа x остаточный член

В самом деле, если x – фиксированное число, то, начиная с некоторого положительного целого числа N, для любого n > N имеем

Следовательно

так как q < 1, а величина  является постоянной при любом n. Таким образом, значения функции e^x могут быть найдены приближенно по формуле:

Разложение функции sin x

Формула Маклорена для функции sin x находится аналогично формуле Маклорена для cos x

Причем

для любого фиксированного вещественного числа x.

47.Дать определение экстремума функции. Сформулировать необходимое и достаточное условия экстремума функции.

Определение 1. Точка  называется точкой максимума [точкой минимума] функции , если существует такая - окрестность  точки , что для всех значений  из этой окрестности выполняется неравенство  

(Необходимое условие экстремума)

Если функция  имеет экстремум в точке , то ее производная  либо равна нулю, либо не существует.

(Первое достаточное условие экстремума)

Пусть для функции  выполнены следующие условия:

1. функция непрерывна в окрестности точки ;

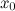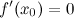2.  или 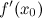 не существует;

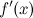3. производная  при переходе через точку 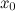 меняет свой знак.

Тогда в точке  функция  имеет экстремум, причем это минимум, если при переходе через точку  производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку  производная меняет свой знак с плюса на минус.

(Второе достаточное условие экстремума)

Пусть для функции  выполнены следующие условия:

1. она непрерывна в окрестности точки ;

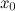2. первая производная 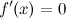 в точке ;

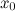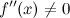3.  в точке  .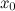

Тогда в точке  достигается экстремум, причем, если , то в точке  функция имеет минимум; если , то в точке  функция  достигает максимум.

48. Дать определение возрастающих и убывающих функций. Сформулировать условия монотонности.

Функция F возрастает на интервале (а;в) если для любых Х1 и Х2 из этого интервала, таких, что Х1 больше Х2, выполняется неравенство F(Х1) больше F (Х2).  Убывает - если F(Х1) меньше F (Х2).

Перечислим свойства монотонных функций (предполагается, что все функции определены на некотором промежутке D).

• Сумма нескольких возрастающих функций является возрастающей функцией.

• Произведение неотрицательных возрастающих функций есть возрастающая функция.

• Если функция f возрастает, то функции cf (c > 0) и f + c также возрастают, а функция cf (c < 0) убывает. Здесь c – некоторая константа.

• Если функция f возрастает и сохраняет знак, то функция 1/f убывает.

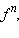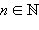• Если функция f возрастает и неотрицательна, то где, также возрастает.

• Если функция f возрастает и n – нечетное число, то f ⁿ также возрастает.

• Композиция g (f (x)) возрастающих функций f и g также возрастает.