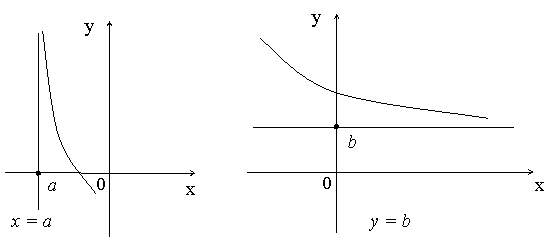- •1.Дать определение компл. Чисел и основных понятий. Что называется модулем и аргументом комплексного числа? Геометрическое изображение компл. Чисел.
- •2. Дать определение комплексных чисел. Записать алгебр., тригонометрич., показат., формы комплексных чисел. Как перейти из одной формы записи в другую?
- •3. Вывести формулы сложения, вычитания, умножения, деления комплексных чисел в алгебраич. Форме.
- •4. . Вывести формулы сложения, вычитания, умножения, деления комплексных чисел в тригонометрич. Форме.
- •5. Записать формулу Муавра, формулу извлечения корня из комплексных чисел. Привести примеры.
- •6. Ввести понятие матрицы. Дать основные определения.
- •7. Дать определение линейных операций над матрицами. Произведение матриц. Приведение матриц к ступенчатому виду.
- •8. Дать определение определителей 2-го, 3-го, n-го порядка. Вычисление определителей. Свойства определителей.
- •9. Дать определение матрицы, обратной к данной. Построить матрицу, обратной к данной.
- •10. Раскрыть метод Крамера решения системы линейных уравнений. Привести пример.
- •11. Раскрыть метод Гаусса решения систем линейных уравнений. Привести пример.
- •12. Раскрыть метод решения систем линейных уравнений с помощью обратной матрицы. Привести пример.
- •13. Определить декартовую систему координат в пространстве. Определить координаты точки в декартовой системе координат.
- •14. Дать определение вектора в пространстве. Определить линейные операции над векторами в геометрической и координатной формах.
- •15. Дать определение скалярного произведения векторов. Записать его свойства. Объяснить геометрический смысл скалярного произведения.
- •16. Дать определение скалярного произведения векторов. Вывести формулу скалярного произведения векторов в координатных формах.
- •17. Дать определение векторного произведения векторов. Записать его свойства. Объяснить геометрич. Смысл.
- •18. Дать определение векторного произведения векторов. Вывести формулу векторного произведения векторов в пространстве.
- •19. Дать определение смешанного произведения векторов. Записать свойства. Вывести формулу спв в координатной форме. Объяснить геометрический смысл спв.
- •21. Вывести параметрическое уравнение прямой на плоскости;
- •22. Вывести формулу для нахождения угла между прямыми на плоскости. Перечислить условие параллельности и перпендикулярности двух прямых. Записать формулу расстояния от точки до прямой.
- •23. Дать определение элипса. Записать каноническое уравнение элипса, основные хар-ки. Изобразить на рисунке.
- •24. Дать определение гиперболы. Записать каноническое уравнение гиперболы, основные хар-ки. Изобразить на рисунке.
- •25. Дать определение параболы. Записать каноническое уравнение параболы, основные характеристики. Изобразить на рисунке.
- •26. Вывести уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору. Вывести общее уравнение плоскости.
- •28. Вывести формулу для определения угла между плоскостями. Записать формулу расстояния от точки до плоскости. Описать варианты взаимного расположения двух плоскостей.
- •29. Вывести уравнение прямой пространства, проходящей через заданную точку параллельно заданному вектору (канонические и параметрические уравнения).
- •30. Определить уравнение прямой, как линии пересечения двух плоскостей. Вывести уравнение прямой, проходящей через две заданные точки.
- •31. Дать определение предела функции в точке и на бесконечности. Определить односторонние пределы. Сформулировать свойства пределов функций. Записать замечательные пределы.
- •32. Показать различные способы вычисления пределов функции в точке и на бесконечности.
- •33. Дать определение функции непрерывной в точке и на промежутке. Перечислить свойства функций непрерывных в точке. Дать определение точек разрыва функции. Классифицировать точки разрыва.
- •34. Дать определение производной функции в точке. Сформулировать её геометрический и физический смысл.
- •35. Сформулировать правила дифференцирования. Вывести формулу производной суммы (разности).
- •36. Сформулировать правила дифференцирования. Вывести формулу производной произведения.
- •37. Сформулировать правила дифференцирования. Вывести формулу производной частного.
- •39. Записать таблицу производных элементарных функций. Вывести производные функций:
- •40. Сформулировать правило нахождения производной сложной функции. Записать таблицу производных сложной функции. Сформулировать правило нахождения производной взаимообратных функций
- •42. Дать определение производной высших порядков. Записать правила нахождения производной второго порядка функции заданной параметричнски, функции заданной неявно. Записать формулу Лейбница.
- •43. Дать определение дифференциала функции. Раскрыть его геометрический смысл. Записать таблицу основных дифференциалов, формулы нахождения дифференциала суммы, произведения, частного
- •44. Сформулировать правила Лопиталя, раскрытия неопределённостей Привести пример
- •45. Сформулировать правила Лопиталя, раскрытия неопределённостей вида Привести пример.
- •47.Дать определение экстремума функции. Сформулировать необходимое и достаточное условия экстремума функции.
- •48. Дать определение возрастающих и убывающих функций. Сформулировать условия монотонности.
- •49. Дать определения выпуклости и вогнутости функции, точек перегиба. Сформулировать достаточное условие выпуклости и вогнутости функций. Сформулировать достаточное условие перегиба функции.
- •50. Дать определение асимптоты графика функции. Перечислить виды асимптот. Записать формулы для их нахождения.
- •51. Составить общую схему исследования функции и построения её графика.
- •52. Вывести понятие функции многих переменных, области определения.
- •53. Дать определение предела функции многих переменных в точке. Непрерывность функции многих переменных.
- •55. Дифференцирование сложной функции многих переменных, дифференцирование неявной функции многих переменных.
- •56. Дать определение частных производных высшего порядка.
49. Дать определения выпуклости и вогнутости функции, точек перегиба. Сформулировать достаточное условие выпуклости и вогнутости функций. Сформулировать достаточное условие перегиба функции.
График
дифференцируемой функции ![]() называется выпуклым вниз (вогнутым) на
интервале (a;b),
если он расположен выше любой её
касательной на этом интервале.
называется выпуклым вниз (вогнутым) на
интервале (a;b),
если он расположен выше любой её
касательной на этом интервале.
График
функции ![]() называется выпуклым вверх на интервале
(a;b),
если он расположен ниже любой её
касательной на этом интервале.
называется выпуклым вверх на интервале
(a;b),
если он расположен ниже любой её
касательной на этом интервале.
Точка
графика непрерывной функции ![]() отделяющая части разной выпуклости
называется точкой перегиба.
отделяющая части разной выпуклости
называется точкой перегиба.
![]()
![]()
0 – точка перегиба
Теорема
1: Если функция ![]() во всех точках интервала (a;b)
имеет отрицательную вторую производную,
т.е.
во всех точках интервала (a;b)
имеет отрицательную вторую производную,
т.е. ![]() ,
то график функции на этом интервале
выпуклый вверх; если
,
то график функции на этом интервале
выпуклый вверх; если ![]() для любого
для любого ![]() ,
то график выпуклой вниз.
,
то график выпуклой вниз.
Теорема
2 (Достаточное условие существования
точки перегиба): Если ![]() при переходе через точку
при переходе через точку ![]() ,
в которой она равна 0 или не существует,
меняет знак, то
,
в которой она равна 0 или не существует,
меняет знак, то ![]() и есть точка перегиба.
и есть точка перегиба.
50. Дать определение асимптоты графика функции. Перечислить виды асимптот. Записать формулы для их нахождения.
Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.
По
способам их отыскания выделяют три вида
асимптот: вертикальные ![]() ,
горизонтальные
,
горизонтальные ![]() ,
наклонные
,
наклонные ![]() .
.
Очевидно, горизонтальные являются
частными случаями наклонных (при ![]() ).
).
|
|
|
|
|
|
|
|
|
Нахождение асимптот графика функции основано на следующих утверждениях.
Теорема
1. Пусть
функция ![]() определена
хотя бы в некоторой полуокрестности точки
определена
хотя бы в некоторой полуокрестности точки ![]() и
хотя бы один из ее односторонних пределов
в этой точке бесконечен, т.е. равен
и
хотя бы один из ее односторонних пределов
в этой точке бесконечен, т.е. равен ![]() или
или ![]() .
Тогда прямая
.
Тогда прямая ![]() является
вертикальной асимптотой графика функции.
является
вертикальной асимптотой графика функции.
Таким образом, вертикальные асимптоты графика функции следует искать в точках разрыва функции или на концах ее области определения (если это конечные числа).
Теорема
2. Пусть
функция ![]() определена
при значениях аргумента, достаточно
больших по абсолютной величине, и
существует конечный предел функции
определена
при значениях аргумента, достаточно
больших по абсолютной величине, и
существует конечный предел функции ![]() .
Тогда прямая
.
Тогда прямая ![]() есть
горизонтальная асимптота графика
функции
есть
горизонтальная асимптота графика
функции ![]() .
.
Может
случиться, что ![]() ,
а
,
а ![]() ,
причем
,
причем ![]() и
и ![]() конечные
числа, тогда график имеет две различные
горизонтальные асимптоты: левостороннюю
и правостороннюю. Если же существует
лишь один из конечных пределов
конечные
числа, тогда график имеет две различные
горизонтальные асимптоты: левостороннюю
и правостороннюю. Если же существует
лишь один из конечных пределов ![]() или
или ![]() ,
то график имеет либо одну левостороннюю,
либо одну правостороннюю горизонтальную
асимптоту.
,
то график имеет либо одну левостороннюю,
либо одну правостороннюю горизонтальную
асимптоту.
Теорема
3. Пусть
функция ![]() определена
при значениях аргумента, достаточно
больших по абсолютной величине, и
существуют конечные пределы
определена
при значениях аргумента, достаточно
больших по абсолютной величине, и
существуют конечные пределы ![]() и
и ![]() .
Тогда прямая
.
Тогда прямая ![]() является
наклонной асимптотой графика функции
является
наклонной асимптотой графика функции ![]() .
.
Заметим, что если хотя бы один из указанных пределов бесконечен, то наклонной асимптоты нет.
Наклонная асимптота так же, как и горизонтальная, может быть односторонней.
Пример.
Найдите все асимптоты графика функции ![]() .
.
Решение.
Функция
определена при ![]() .
Найдем ее односторонние пределы в
точках
.
Найдем ее односторонние пределы в
точках ![]() .
.
Так
как ![]() и
и ![]() (два
других односторонних предела можно уже
не находить), то прямые
(два
других односторонних предела можно уже
не находить), то прямые ![]() и
и ![]() являются
вертикальными асимптотами графика
функции.
являются
вертикальными асимптотами графика
функции.
Вычислим
![]() (применим
правило Лопиталя)
=
(применим
правило Лопиталя)
=
![]() .
.
Значит,
прямая ![]() горизонтальная
асимптота.
горизонтальная
асимптота.
Так как горизонтальная асимптота существует, то наклонные уже не ищем (их нет).
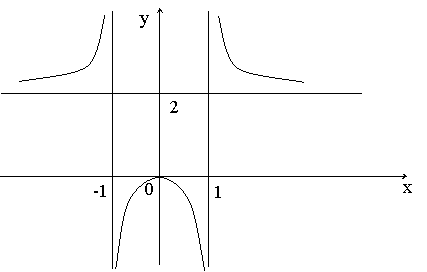 Ответ:
график имеет две вертикальные асимптоты
Ответ:
график имеет две вертикальные асимптоты ![]() и
одну горизонтальную
и
одну горизонтальную ![]() .
.